康威生命游戏

题目：康威生命游戏
分类：数组、矩阵、模拟
根据 百度百科 ， 生命游戏 ，简称为 生命 ，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。
给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：
1.如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
2.如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
3.如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
4.如果死细胞周围正好有三个活细胞，则该位置死细胞复活；
下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。
示例 1：
输入：board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出：[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
示例 2：
输入：board = [[1,1],[1,0]]
输出：[[1,1],[1,1]]
提示：
m == board.length
n == board[i].length
1 <= m, n <= 25
board[i][j] 为 0 或 1

思路

• 源自题解，也是容易忽视的，导致后续数据被污染，部分出错；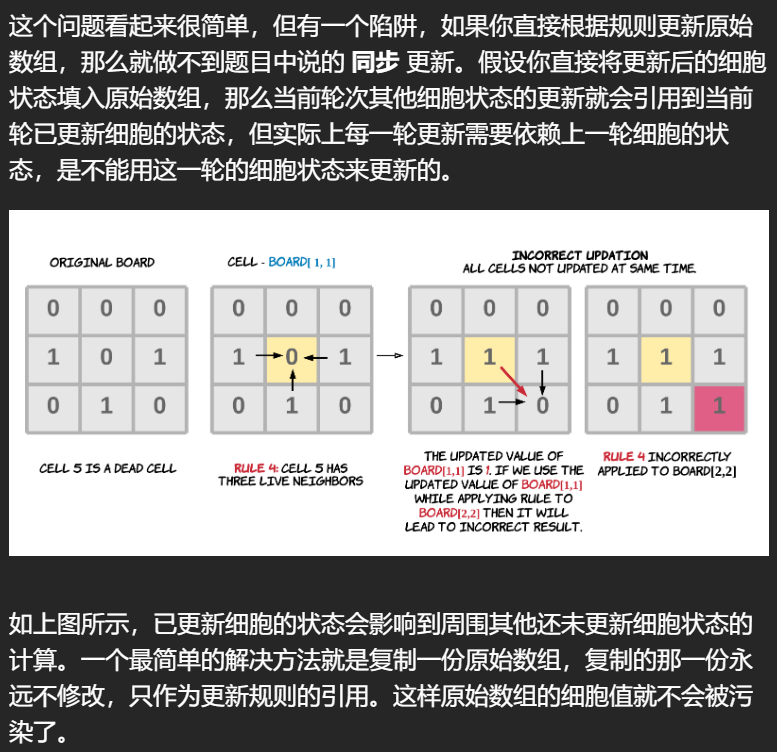

此处复制一个newboard,所有的检索均针对newborad[i][j],在本元素的值确认后赋给board[i][j]

• 鉴于对每个元素来说，都要检测8个邻居，可以看作三行三列，除开自己，而这里需要用本身来表示邻居，明显有-1、0、1的关系（行与列均是如此），所以可以共用一个偏移量skewing来表示邻居的行与列，分别是

• 根据规则对live++

• 注意此时skewing[s]和skewing[t]代表的是偏移的量
  

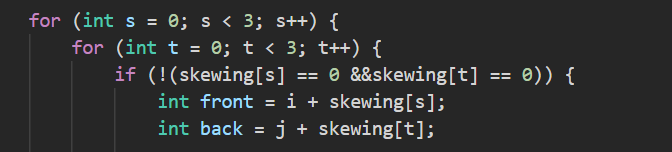
  当skewing[s]和skewing[t]都为0时，我们实际上并没有检查任何邻居。这种情况发生在当前细胞位于边界或角落时，它只有1或2个邻居。在这种情况下，我们不需要更新该细胞的状态，因为它的邻居数量已经符合上述规则。

• 这里区分一个经典出错
  !((a == b) && (c == d)) 和 (a != b) && (c != d)

  • 对于 !((a == b) && (c == d))：
    此表达式取真的条件是当 a 不等于 b 或者 c 不等于 d。即如果两对比较中至少有一对不相等，则此表达式为真。
    用逻辑表达式来表示就是： !((a == b) && (c == d)) 等价于 (a != b) || (c != d)，根据德摩根定律。
  • 对于 (a != b) && (c != d)：
    此表达式取真的条件是当 a 不等于 b 且 c 不等于 d。即两对比较都必须不满足相等关系，此表达式才为真。
    这两个表达式虽然在某种程度上是逻辑等价的，但它们在具体实现上有着细微的差异。

/*java*/

class Solution {
    public void gameOfLife(int[][] board) {
        int m = board.length;
        int n = board[0].length;
        int live = 0;
        int[] skewing = {-1，0，1};
        int[][] newboard = new int[m][n];
        //i即newboard的行,j即newboard的列
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                newboard[i][j] = board[i][j];
            }
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                live = 0; // 重置 live 计数器
				/*扫描8个元素*/
                for (int s = 0; s < 3; s++) {
                    for (int t = 0; t < 3; t++) {
                        if (!(skewing[s] == 0 && skewing[t] == 0)) {
                            int front = i + skewing[s];
                            int back = j + skewing[t];

                            if (front >= 0 && front < m && back >= 0 && back < n ) {
                                if(newboard[front][back] == 1)
                                    live++;
                            }
                        }
                    }
                }

                if (newboard[i][j] == 1) {
                    if (live < 2 || live > 3) {
                        board[i][j] = 0;
                    }
                } else if (live == 3) {
                    board[i][j] = 1;
                }
            }
        }
    }
}