Graph Classification mini-batch 训练方法
参考资料
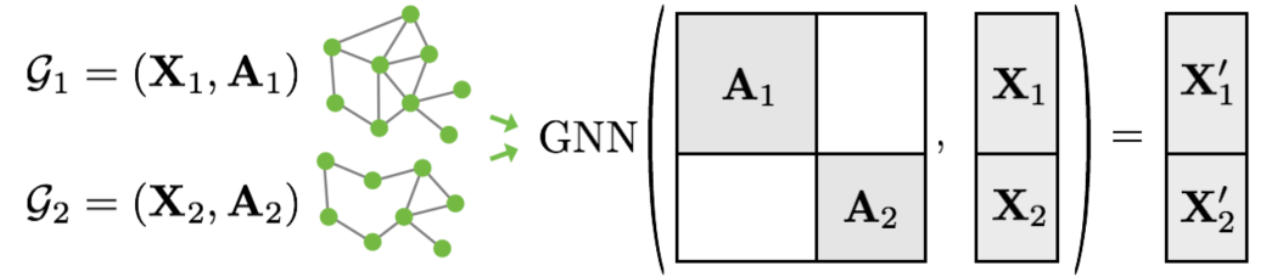
PyTorch Geometric opts for another approach to achieve parallelization across a number of examples. Here, adjacency matrices are stacked in a diagonal fashion (creating a giant graph that holds multiple isolated subgraphs), and node and target features are simply concatenated in the node dimension:
做法:
- 每个图独立:
train_graphs = []
for g_idx in range(len(adj)):
edge_index, edge_weight = adj2edge_info(adj[g_idx])
train_graphs.append(Data(x=input[g_idx],
edge_index=edge_index, edge_weight=edge_weight))
# way 1
train_loader = DataLoader(train_graphs, batch_size=2, shuffle=False)
for step, data in enumerate(train_loader):
input, edge_index = data.x, data.edge_index
input = torch.reshape(input, (input.shape[0], -1))
logits = gnn(input, edge_index, data.batch)
print(logits)
# way 2
batch_data = Batch.from_data_list(train_graphs)
input, edge_index = batch_data.x, batch_data.edge_index
input = torch.reshape(input, (input.shape[0], -1))
logits = gnn(input, edge_index, batch_data.batch)
print(logits)
- 每个图的结构相同,节点属性不同:
# You have two options here: (1) Replicating your `edge_index` by stacking them diagonally, _e.g._, via:
batch_edge_index = Batch.from_data_list([Data(edge_index=edge_index)] * batch_size)
# or using the `node_dim` property of message passing operators:
conv = GCNConv(in_channels, out_channels, node_dim=1)
conv(x, edge_index) # here, x is a tensor of size [batch_size, num_nodes, num_features]