谱GNN卷积和信号处理的关系
结论
- 信号处理中的傅立叶变换,将一个复杂信号分解为多个已知频率的波 \(<==>\) 对应图信号中将\(x\)分解到不同频率(特征值)的特征向量上。
- 信号中的卷积定理说明了:时域上的卷积等于频域上的点积。\(<==>\) 对应GNN中,两个图信号的卷积 等于它们分解到特征空间\(U\)上的系数之间进行点积 再进行傅立叶的逆变换。
- 从数学上,卷积是一种运算,可以直接利用定义进行计算;但是可以用卷积定理降低复杂度,进行等价计算。
信号处理
信号卷积
-
连续形式
\[(f*g)(t) = \int_{-\infty}^{+\infty} f(x)g(t-x) dx \] -
离散形式
\[(f*g)(t) = \sum_{x=-\infty}^{+\infty} f(x)g(t-x) \] -
离散情况下两个信号卷积计算例子(图源)
下例中的k和公式中的t对应
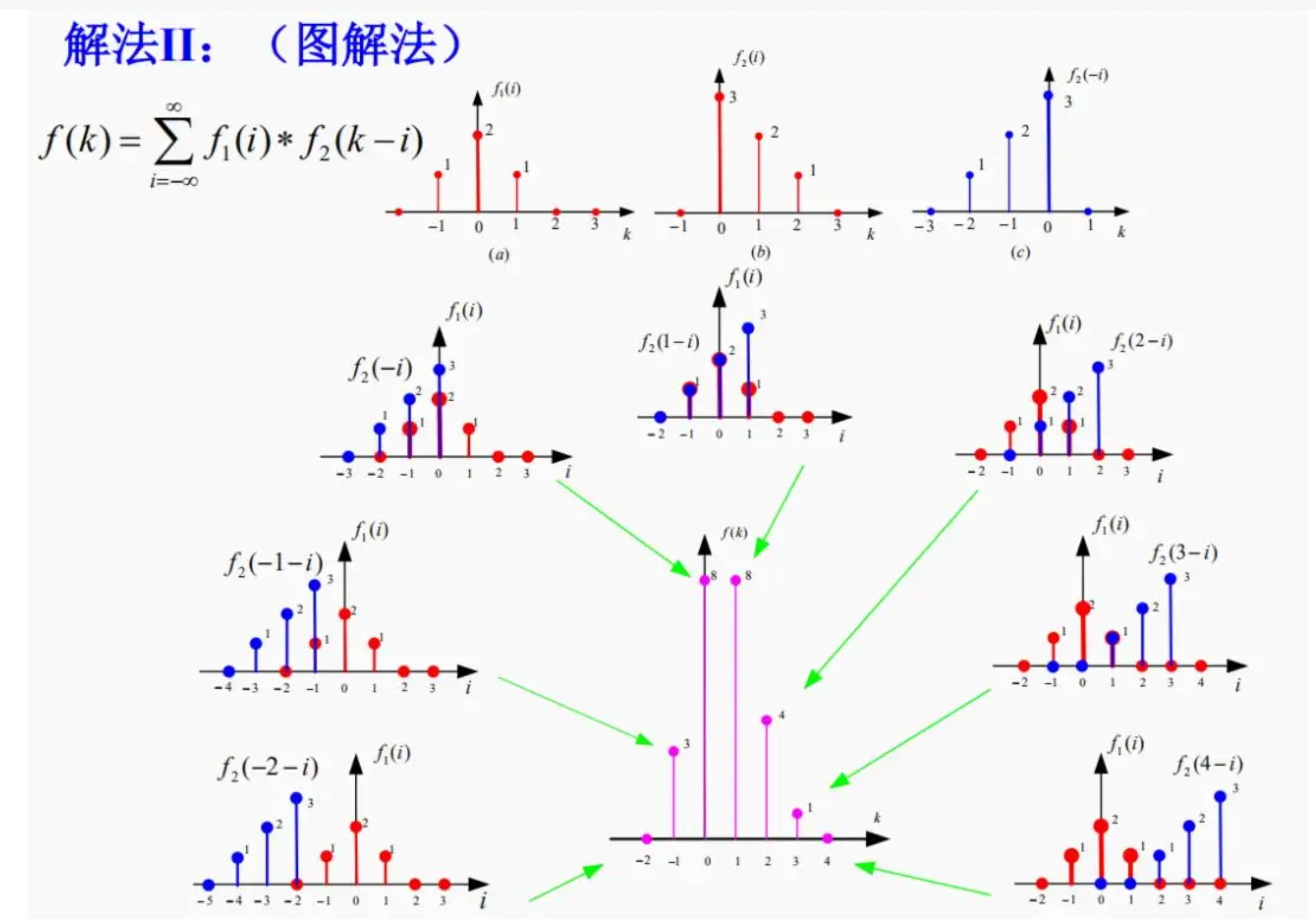
下图中我们想对图(a)的\(f_1\)信号和图(b)的\(f_2\)信号进行卷积,通过离散卷积定义,我们先将\(f_2(i)\)(图b)变成\(f_2(-i)\)(图c),然后在\(-\infty\)和\(+\infty\)的区间上平移k步变成\(f_2(k-i)\),对于每一个\(f_2(k-i)\),我们将其和\(f_1(x)\)对位相乘再求和,得到的结果\(f(k)\)标记在粉色的图上(横坐标为\(k\), 纵坐标位\(f(k)\)).
- 例如:当k=0的时候,我们将\(f_1(i)\)和\(f_2(-i)\)画到同一个坐标系上,如图b下面的那个图,对位相乘再相加,即\(0*(-2)+1*1+2*2+1*3+2*0+3*0=8\),因此粉色图上\(f(0)=8\)。
- 虽然我们是在\(-\infty\)和\(+\infty\)的区间上对\(f_2(-i)\)进行平移,但是对于下例中对于\(k<-2\)或者\(k>4\)的时候,计算出来的\(f(k)=0\),因此在粉色图上没有表示。
傅立叶变换
- 傅立叶变换:能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。\[F(\omega)=\mathcal{F}[f(t)]=\int_{-\infty}^{\infty} f(t) e^{-iwt} dt \]
卷积定理
-
\[\mathcal{F}[f*g]=\mathcal{F}[f] \cdot \mathcal{F}[g] \\ f*g=\mathcal{F}^{-1}[\mathcal{F}[f] \cdot \mathcal{F}[g]] \]
-
证明(参考)

GNN
图傅立叶变换
-
图傅立叶变换
\[\hat{f} = U^T f \] -
图傅立叶逆变换
\[f = U f \] -
图傅立叶变换解释(图片来源)
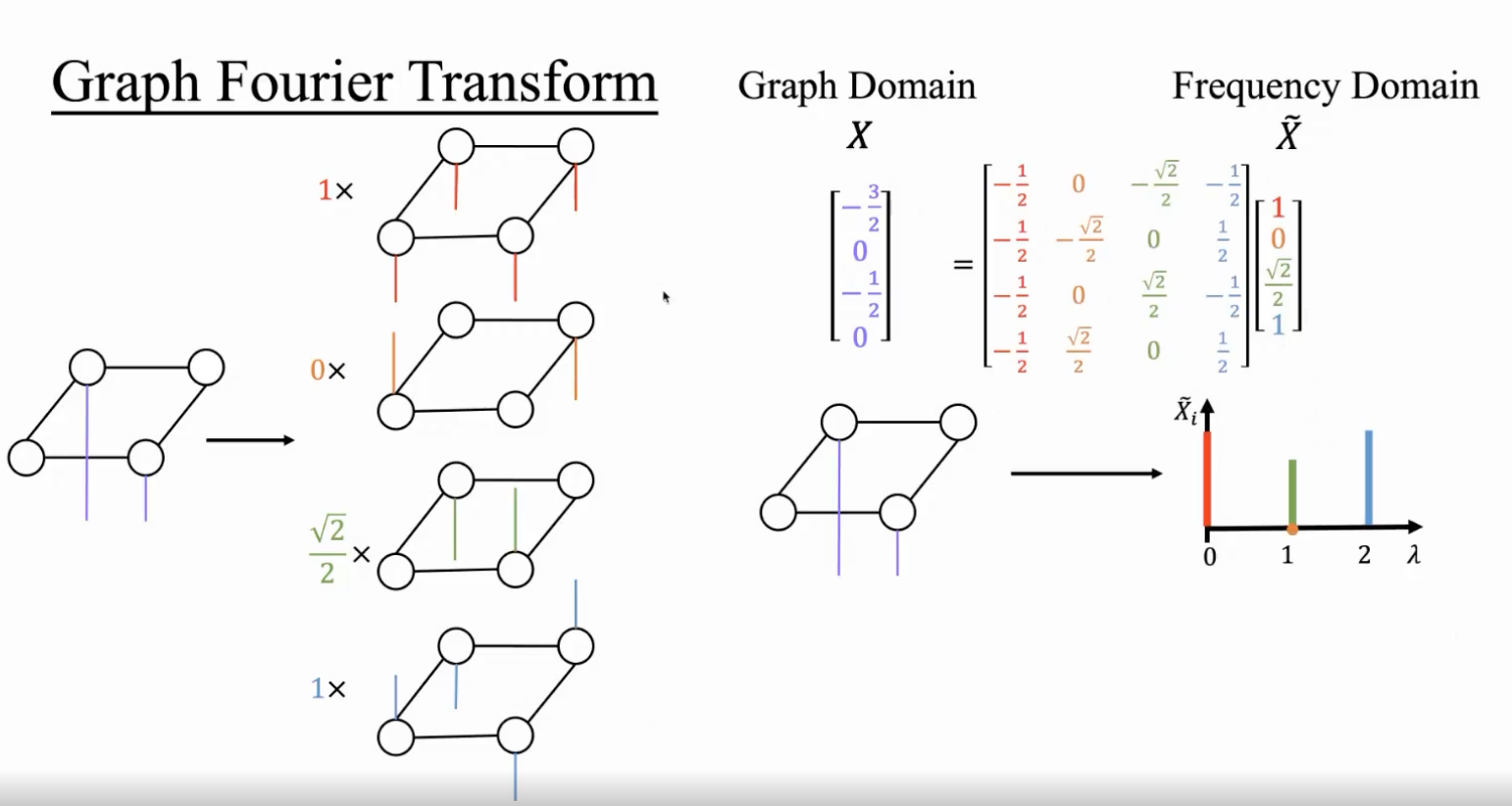
如下图所示,对一个信号进行图傅立叶变换,其实是将其分解到各个特征值对应的特征向量上,下图中紫色的是图上的一个信号,其他颜色代表不同的特征向量,数字代表的是分解后的系数。而我们知道特征值就代表了特征向量的频率,即平滑程度,越平滑频率越低特征值越小,因此可以和信号中的傅立叶变换对应。
- 这里的平滑是指 所有相连节点的表示相同
图卷积
-
图卷积定理
\[g*x = U((U^Tg) \odot (U^Tx)) \] -
解释
图傅立叶变换是将信号分解到不同频率的特征向量上,其中不同的特征向量对应的平滑程度不一样(如最小特征值对应的特征值是0,特征向量是一个全1的向量,如上图红色,因此所有相连节点的特征都是相同的,因此是绝对平滑,频率为0)。所以这里我们想要对通过调整分解后不同特征向量对应系数的高低,来达到对信号过滤的效果,比如增加低频向量的权重会使得相邻节点的表示更加相近,增加高频的表示会使得相邻节点的表示更远。\(U^Tg\)其实就是起到了一个对系数进行调整的作用,也称为滤波器。
\(L\)矩阵特征值和特征向量
拉普拉斯矩阵的特征值描述了特征向量的平滑程度:
\[\lambda_i = \lambda_i u^T u = u^T Lu = \frac{1}{2} \sum_{v_i \in V} \sum_{v_j \in N(v_i)} (u[i]-u[j])^2
\]
证明如下:



