帕累托分布&广义帕累托分布
PDF、PMF、CDF
1. 概念解释
- PDF:概率密度函数(probability density function), 在数学中,连续型随机变量的概率密度函数(在不至于混淆时可以简称为密度函数)是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。
- PMF:概率质量函数(probability mass function), 在概率论中,概率质量函数是离散随机变量在各特定取值上的概率。
- CDF:累积分布函数 (cumulative distribution function),又叫分布函数,是概率密度函数的积分,能完整描述一个实随机变量X的概率分布。
2. 数学表示
2.1 PDF
如果XX是连续型随机变量,定义概率密度函数为,用PDF在某一区间上的积分来刻画随机变量落在这个区间中的概率,即
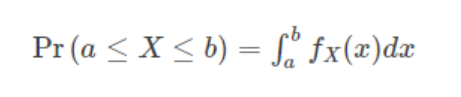
2.2 PMF
如果XX离散型随机变量,定义概率质量函数为,PMF其实就是高中所学的离散型随机变量的分布律,即
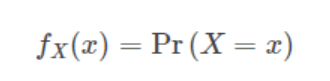
2.3 CDF
不管是什么类型(连续/离散/其他)的随机变量,都可以定义它的累积分布函数,有时简称为分布函数。
Pareto(帕累托)分布
Survial function 生成函数
The survival function is also known as the survivor function[2] or reliability function.[3]
又称 complementary cumulative distribution function.
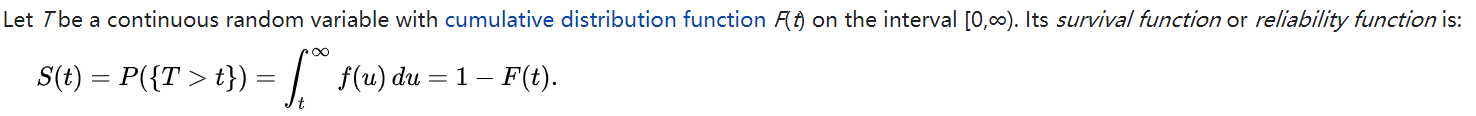
其实就是1-CDF
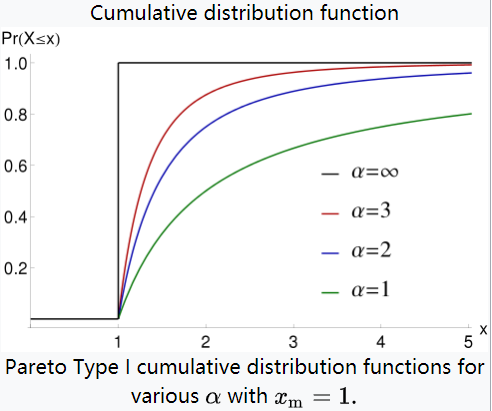
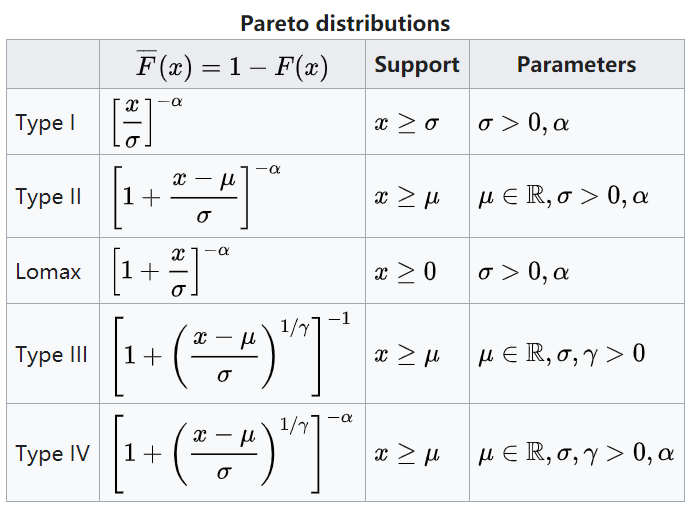
Pareto distribution

- 注意形状参数必须是正的!

Generalized Pareto distribution
https://en.wikipedia.org/wiki/Generalized_Pareto_distribution

因此,GP 分布是指数分布 (k = 0) 和帕累托分布 (k>0) 的广义化。GP 将这两个分布包括在更大的族中,因此可以实现连续的形状范围。
Matlab实现
利用广义帕累托分布对尾数据建模
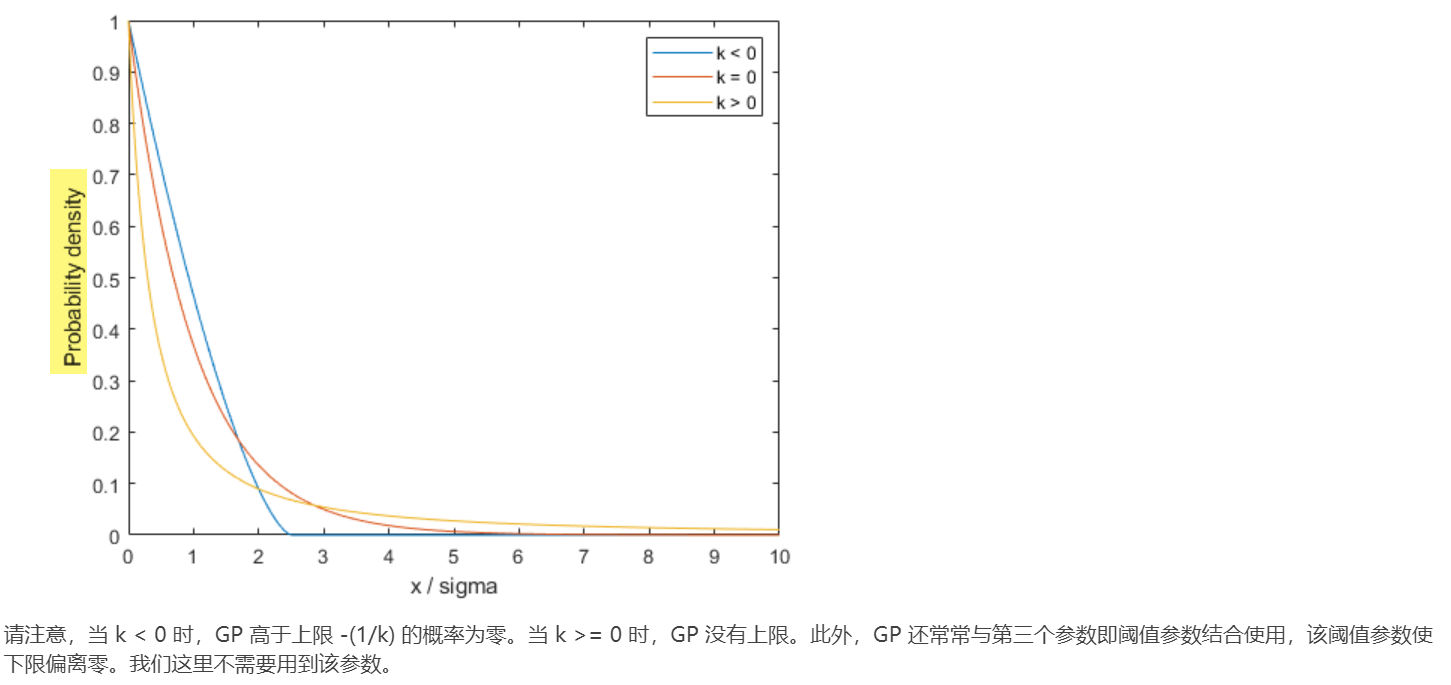
广义帕累托 (GP) 分布是一种右偏态分布,使用形状参数 k 和尺度参数 sigma 进行参数化。k 也称为“尾部指数”参数,可以为正值、零或负值。
x = linspace(0,10,1000);
plot(x,gppdf(x,-.4,1),'-', x,gppdf(x,0,1),'-', x,gppdf(x,2,1),'-');
xlabel('x / sigma');
ylabel('Probability density');
legend({'k < 0' 'k = 0' 'k > 0'});
其他代码见链接!

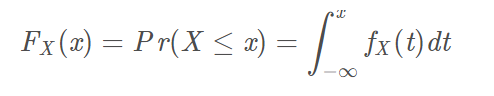
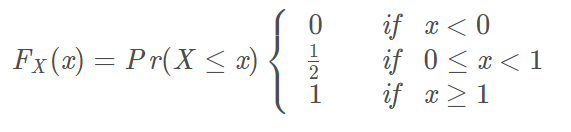




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通