数据结构-堆

二叉堆

二叉堆是完全二元树或者是近似完全二元树，按照数据的排列方式可以分为两种：最大堆和最小堆。

最大堆

父结点的键值总是大于或等于任何一个子节点的键值

最小堆

父结点的键值总是小于或等于任何一个子节点的键值。

1添加

假设在最大堆[90,80,70,60,40,30,20,10,50]种添加85，需要执行的步骤如下：

 

 

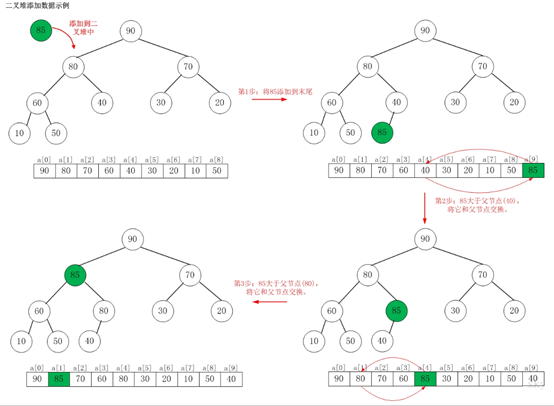
如上图所示，当向最大堆中添加数据时：先将数据加入到最大堆的最后，然后尽可能把这个元素往上挪，直到挪不动为止！
将85添加到[90,80,70,60,40,30,20,10,50]中后，

最大堆变成了[90,85,70,60,80,30,20,10,50,40]。

 

2. 删除

假设从最大堆[90,85,70,60,80,30,20,10,50,40]中删除90，需要执行的步骤如下：

 

 

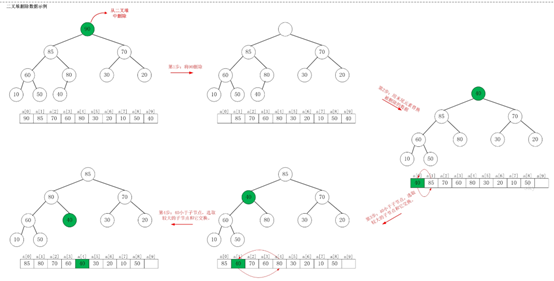
如上图所示，当从最大堆中删除数据时：先删除该数据，然后用最大堆中最后一个的元素插入这个空位；接着，把这个“空位”尽量往上挪，直到剩余的数据变成一个最大堆。
从[90,85,70,60,80,30,20,10,50,40]删除90之后，最大堆变成了[85,80,70,60,40,30,20,10,50]。

 

左倾堆

和二叉堆一样，都是优先队列的实现方式。当优先队列中涉及到“对两个优先队列进行合并”的问题时，二叉堆的效率就无法令人满意了，而本文介绍的左倾堆，则可以很好地解决这类问题

节点属性：

左子树，右子树，键值，零距离

键值：用来比较节点的大小，从而对节点进行排序

零距离：从一个节点到一个“最近的不满节点”的路径长度。不满节点是指该节点的左右孩子至少有一个为null。叶子节点的NPL为0，NULL节点的NPL为-1。

 

左倾堆的性质：

节点的键值小于或等于它的左右子节点的键值

节点的左孩子的NPL >= 右孩子的NPL

节点的NPL = 它的右孩子的NPL+1

 

 

左倾堆的合并

1） 如果一个空左倾堆与一个非空左倾堆合并，返回非空左倾堆

2） 如果两个左倾堆都非空，那么比较两个根节点，取较小堆的根节点为新的根节点。将较小堆的根节点的右孩子和“较大堆”进行合并。

3） 如果新堆的右孩子的NPL >= 左孩子的NPL,则交换左右孩子。

4） 设置新堆的根节点的NPL = 右子堆NPL +1

 

演示用例：

 

 

第1步：将"较小堆(根为10)的右孩子"和"较大堆(根为11)"进行合并。
合并的结果，相当于将"较大堆"设置"较小堆"的右孩子，如下图所示：

 

 

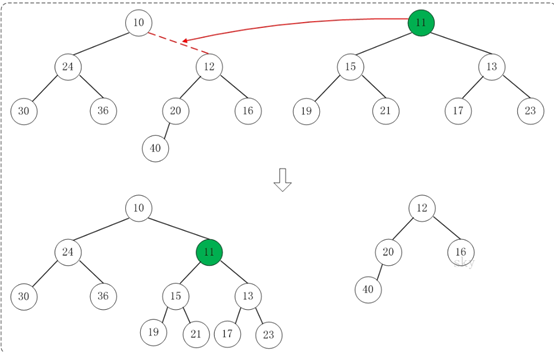
第2步：将上一步得到的"根11的右子树"和"根为12的树"进行合并，得到的结果如下：

 

 

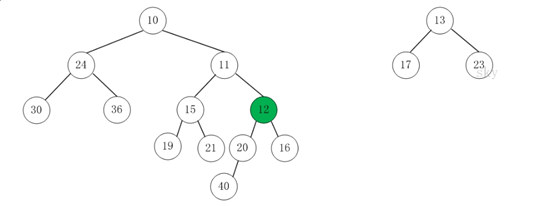
第3步：将上一步得到的"根12的右子树"和"根为13的树"进行合并，得到的结果如下：

 

 

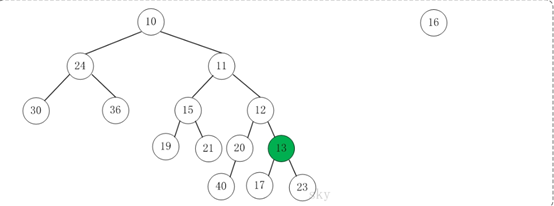
第4步：将上一步得到的"根13的右子树"和"根为16的树"进行合并，得到的结果如下：

 

 

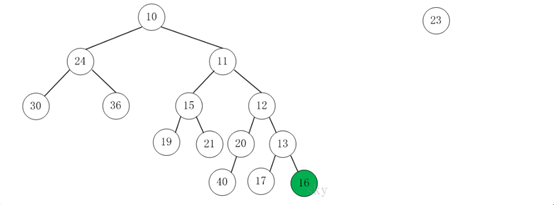
第5步：将上一步得到的"根16的右子树"和"根为23的树"进行合并，得到的结果如下：

 

 

至此，已经成功的将两棵树合并成为一棵树了。接下来，对新生成的树进行调节。

第6步：上一步得到的"树16的右孩子的NPL > 左孩子的NPL"，因此交换左右孩子。得到的结果如下：

 

 

第7步：上一步得到的"树12的右孩子的NPL > 左孩子的NPL"，因此交换左右孩子。得到的结果如下：

 

 

第8步：上一步得到的"树10的右孩子的NPL > 左孩子的NPL"，因此交换左右孩子。得到的结果如下：

 

 

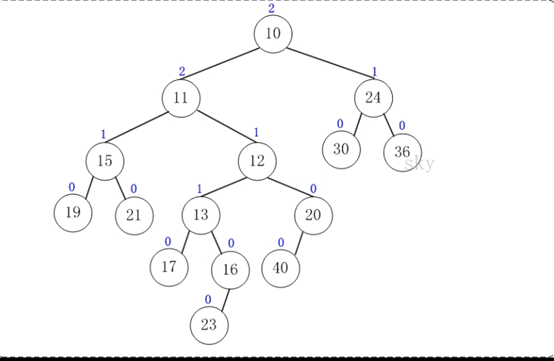
至此，合并完毕。上面就是合并得到的左倾堆！

 

斜堆

斜堆(Skew heap)也叫自适应堆(self-adjusting heap)，它是左倾堆的一个变种。和左倾堆一样，它通常也用于实现优先队列；作为一种自适应的左倾堆，它的合并操作的时间复杂度也是O(lg n)。

斜堆与左倾堆的差别是：
(01) 斜堆的节点没有"零距离"这个属性，而左倾堆则有。
(02) 斜堆的合并操作和左倾堆的合并操作算法不同。

斜堆的合并操作
(01) 如果一个空斜堆与一个非空斜堆合并，返回非空斜堆。
(02) 如果两个斜堆都非空，那么比较两个根节点，取较小堆的根节点为新的根节点。将"较小堆的根节点的右孩子"和"较大堆"进行合并。
(03) 合并后，交换新堆根节点的左孩子和右孩子。
       

第(03)步是斜堆和左倾堆的合并操作差别的关键所在，如果是左倾堆，则合并后要比较左右孩子的零距离大小，若右孩子的零距离 > 左孩子的零距离，则交换左右孩子；最后，在设置根的零距离。