CSP图论一
CSP 图论一
图论〔Graph Theory〕是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。
图的建图方式
想要对图进行操作,就需要先学习图的存储方式。
目前常用的图的存储方式有两种,邻接矩阵和邻接表存储。边数M相对小(远远小于n*(n-1))的图为稀疏图,反之为稠密图。稀疏图可用邻接表存储,稠密图可用邻接矩阵存储。邻接表可用数组或链表实现,邻接矩阵可用二维数组实现
链式前向星
本质上是用链表实现的邻接表,核心代码如下:
链式前向星存储包括两种结构:
边集数组:edge[] , edge[i]表示第i条边
头结点数组:head[] , head[i]存以i为起点的第一条边
ne[]:指向下一条过一个起点的边。
加边过程:
初始时:head[u]=cnt=0;
struct Edge
{
int ne, to, w;//下一个节点,指向的点,边的权值
} edge[N];
int h[N],cnt;//头结点,边的个数
void add(int a,int b,int c)//新增一条边
{
++cnt;//为该边进行编号
edge[cnt].to = b;//边(a,b)
edge[cnt].w = c;
edge[cnt].ne = h[a];//第cnt条边与前面已经连的cnt-1条边相连,并由第cnt边指向第cnt-1边
h[a] = cnt;//更新a的起始边。
}
如果还难以理解,可参考下列两张图:


加边操作:
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
add(u,v,w);
...
}
遍历方式
for (int i = h[u]; i; i = edge[i].ne)//最后终点指向的是0.
{
int v = edge[i].to;
...
}
邻接矩阵
使用一个二维数组 w来存边, 顶点自身到自身的权值默认为0,若该边不存在,就存为无穷大。
int w[N][N];
int main()
{
int n;
cin >> n;
for(int i = 1;i <= n;i++) //矩阵初始化
{
for(int j = 1;j <= n;j++)
{
if(i == j)
w[i][j] = 0; //自身存为0
else
w[i][j] = INF; //其他边为无穷
}
}
for (int i = 1; i <= n;i++)
{
int a, b, c;
cin >> a >> b >> c;
w[a][b] = c;
}
return 0;
}
最小生成树
在一给定的无向图G = (V, E) 中,(u, v) 代表连接顶点 u 与顶点 v 的边,而 w(u, v) 代表此的边权重,若存在 T 为 E 的子集(即)且为无循环图,使得的 w(T) 最小,则此 T 为 G 的最小生成树。最小生成树其实是最小权重生成树的简称。(简而言之就是把一个图变成一棵树,并且树中的边权和最小)

Prim算法
prim算法基于贪心,我们每次总是选出一个离生成树距离最小的点去加入生成树,最后实现最小生成树(不做证明,理解思想即可)

我们构建两个集合,一个集合S(红色),一个集合V(蓝色),S中存放的是已经加入最小生成树的点,V中存放的是还没有加入最小生成树的点,显然刚开始所有的点都在V中
我们先将任意一个点加入到S中,这里默认为点1,并且初始化所有点(除点1)到集合S的距离为无穷大


用一个变量res存放最小生成树所有边权值的和。我们每次都选择离S集合最近的点加入S集合中,并且用新加入的点去更新dist数组,因为只有一个新的点加入到集合S中,到集合S的距离才有可能更新(贪心,每次都选最小的)。
更新就是看一下能否通过新加入的点使到达集合的距离变小(看下面dist数组的变化)。
我们开始在加入点1后开始第一次更新。

现在集合S={1},集合V={2,3,4,5,6,7},根据贪心策略,我们选择离集合S最近的点加入 ,即点2,并把这一条边的权值加到res中。
 '
'
集合更新为S={1,2},V={3,4,5,6,7},并用点2去更新dist数组,我们发现点3和点7都可以都可以通过边2-3,2-7缩短到集合S得距离。

重复上面的步骤,直到将全部的点加入到最小生成树中。









于是我们构建了一个权值和是57最小生成树。
以下是Prim算法的实现代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N=5e3+10,INF=0x3f3f3f3f;
int n, m, w[N][N], dist[N], vis[N];
int prim()
{
memset(dist, 0x3f, sizeof dist);//距离一开始为正无穷
int res = 0;
for (int i = 0; i < n;i++)
{
int t = -1;//接下来去寻找离集合S最近的点加入到集合中,用t记录这个点的下标。
for (int j = 1; j <= n;j++)
{
if(!vis[j]&&(t==-1 || dist[t] > dist[j]))
t = j;
}
if(i&&dist[t]==INF)//在集合V找不到边连向集合S,生成树构建失败,将res赋值正无穷表示构建失败,结束函数
return INF;
if(i)
res += dist[t];
for (int j = 1; j <= n;j++)
{
dist[j] = min(dist[j], w[t][j]);//用新加入的点更新dist
}
vis[t] = 1;
}
return res;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m;
memset(w, 0x3f, sizeof w);//初始化边为正无穷
for (int i = 1; i <= m;i++)
{
int a, b, c;
cin >> a >> b >> c;
w[a][b] = w[b][a] = min(w[a][b],c);//防止重边
}
int ans = prim();
if(ans == INF)
cout << "orz";
else
cout << ans;
return 0;
}
Kruskal算法
kruskal算法虽然也是从贪心的角度实现的,但实现方式却与prim算法差异很大。
其算法复杂度为O(mlogm),适合处理稀疏图。
算法过程:
图中给出n个点,m条边:
1.先将边按照边权从小到大排序,并建立张空图G。
2.选出一条没有被选过且边权最小的边。
3.如果这条边的两个顶点在G所在的连通块不相同,则将其加入图G中,如果相同,这跳过。
4.重复2,3,直到有n-1条边或遍历所有边后为止。
实现过程中可采用并查集来实现。
还是上图例子:
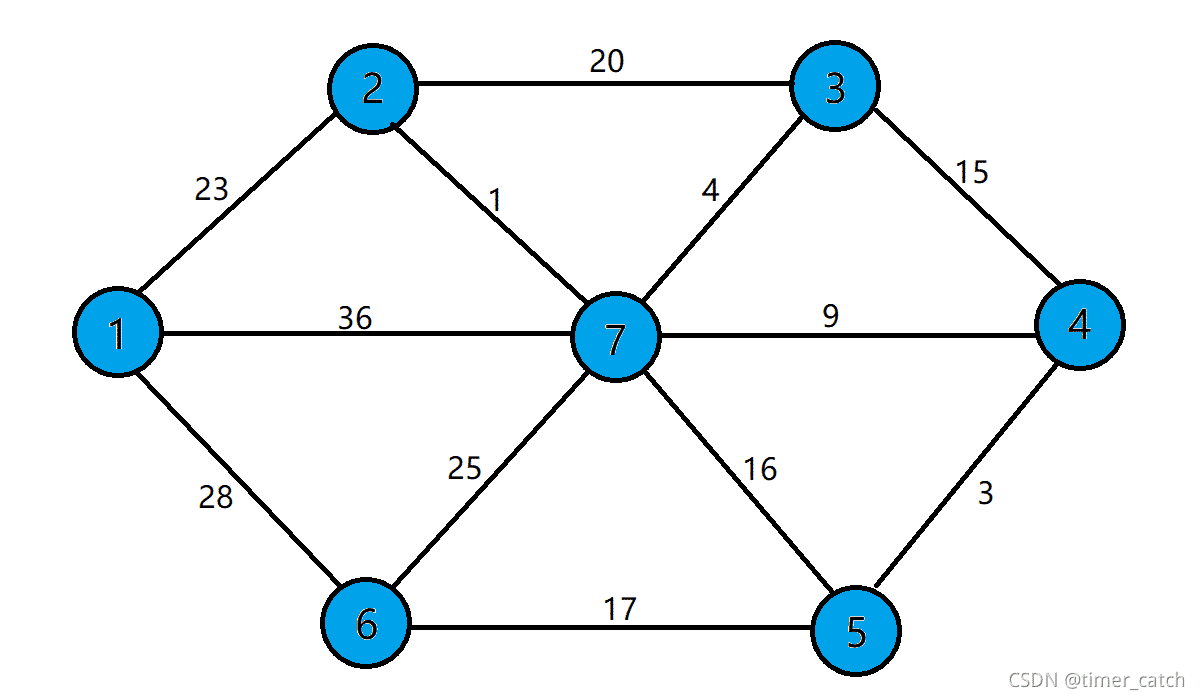
对边进行排序:
(2,7,1),(4,5,3),(3,7,4),(4,7,9),(3,4,15),(5,7,16),
(5,6,17),(2,3,20),(1,2,23),(6,7,25),(1,6,28),(1,7,36)。
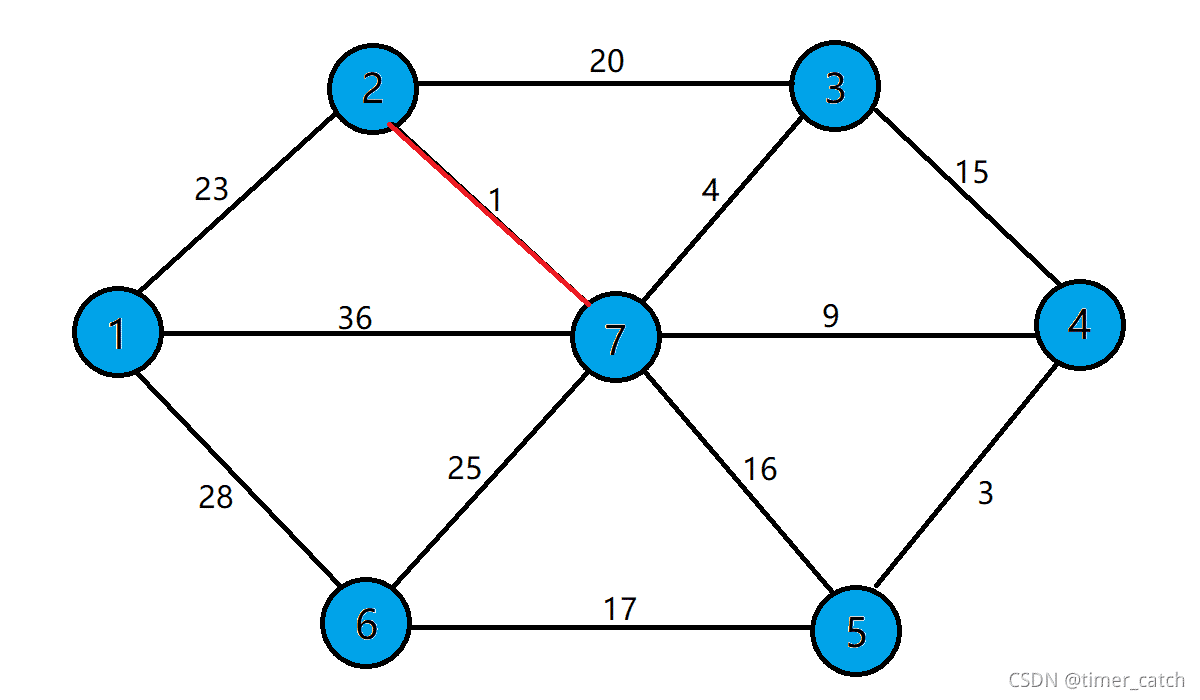
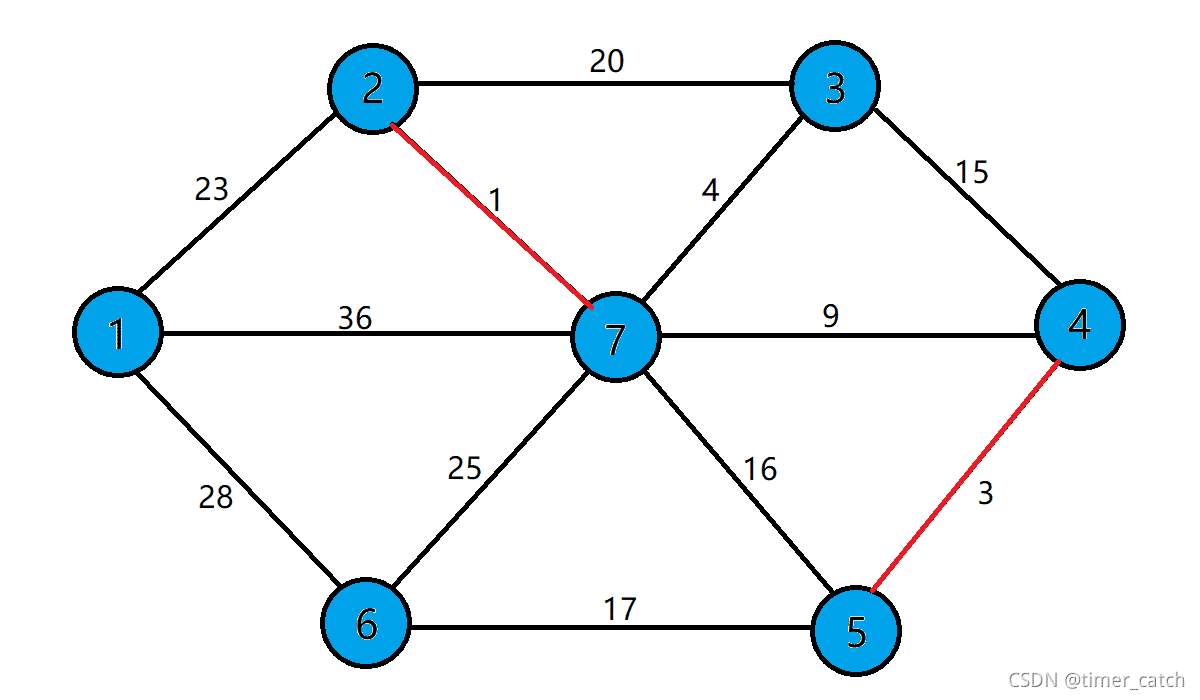

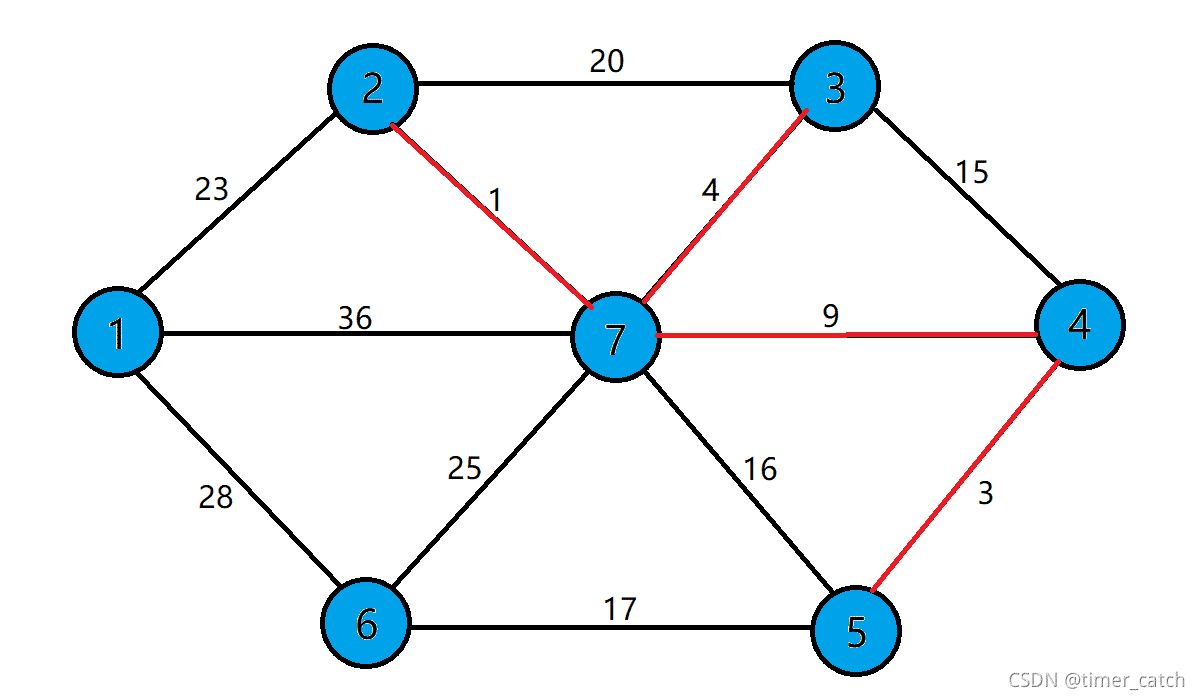

注:这里边(3,4)是不可选的,因为点3,4以及在同一个连通块了,下图也是如此

最后得到完整最小生成树。
并查集
定义:
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题(即所谓的并、查)。比如说,我们可以用并查集来判断某个节点是否属于某棵树等操作。
常见操作:
1.将两个集合合并
2.查询某个元素的祖宗节点
基本原理:每个集合用一棵树来表示。树根的编号就是整个集合的编号。每个节点存储它的父节点,father[]表示父节点
问题1:如何判断树根:if(father[x] == x) (x的父节点指向自己)
问题2:如何求x的集合编号(求x的祖宗节点)(集合编号是这个集合的代表):while(father[x] != x ) x = father[x]
问题3:如何合并两个集合:将x的根节点嫁接到y的根节点,如:px是x的集合编号,py是y的集合编号,嫁接:father[px] = y
并查集的初始化:
for(int i = 0; i < n; i ++) fa[i] = i;//每个节点的父节点一开始都指向自己

查找x的祖宗节点:
如何求x的集合编号(求x的祖宗节点):while(father[x] != x ) x = father[x]:每每寻找新的x的祖宗节点都要重新从当前位置遍历逐一寻找父节点直至得到祖宗节点,时间复杂度O(n),当数据量很庞大时,效率就会比较低。这条搜索路径可能很长。如果在返回的时候,顺便把i所属的集改成根结点,那么下次再搜的时候,就能在O(1)的时间内得到结果。可以通过查找 + 路径压缩的方式优化到近乎O(1)的时间复杂度。
并查集优化:查找 + 路径压缩

find函数的功能是查找祖宗节点,路径压缩的过程其实是一个递归调用与回溯的过程!在递归过程中,从元素i到根结点的所有元素,它们所属的集都被改为根结点。路径压缩不仅优化了下次查询,而且也优化了合并,因为合并时也用到了查询。

int find(int x)// 返回x的祖先节点 + 路径压缩
{
// x不是根节点,让它的父节点等于(指向)祖宗节点
// x 不是自身的父亲,即 x 不是该集合的代表
if(fa[x] != x) fa[x] = find(fa[x]);
// 返回x的祖先节点
return fa[x];
}
合并集合
fa[find(a)] = find(b);//a的祖先节点的父节点修改为b的祖先节点

判断两个元素是否在一个集合中
if(find(a) == find(b))//a和b的祖先节点是否相同,如果相同那么它们处于同一集合
学习并查集后,可以用并查集实现Kruskal算法,从而求得最小生成树。
Kruskal算法求最小生成树:
#include<bits/stdc++.h>
const int maxn = 1e6 + 1;
using namespace std;
int n, m;
struct node{
int u;
int v;
int w;
}e[maxn];
int fa[maxn], cnt, sum, num;
void add(int x, int y, int w)
{
e[++ cnt].u = x;
e[cnt].v = y;
e[cnt].w = w;
}//链式前向星建边
bool cmp(node x, node y)
{
return x.w < y.w;
}
int find(int x)//查询祖宗节点+路径压缩
{
if(fa[x] != x) fa[x] = find(fa[x]);
return fa[x];
}
void kruskal()
{
for(int i = 1; i <= cnt; i ++)
{
int x = find(e[i].u);//找到u的祖宗的节点
int y = find(e[i].v);//找到v的祖宗节点
if(x == y) continue;//如果它们的祖宗节点相同则不需要合并
fa[x] = y;//合并操作
sum += e[i].w;
if(++ num == n - 1) break;//如果构成了一颗树就退出
}
}
int main()
{
cin>>n>>m;
for(int i = 1; i <= n; i ++) fa[i] = i;
while(m --)
{
int x, y, w;
cin>>x>>y>>w;
add(x, y, w);//添加一条边
}
sort(e + 1, e + 1 + cnt, cmp);//按边权从小到大进行排序
kruskal();
printf("%d",sum);
return 0;
}
最短路
所谓最短路是指:如果从图中某一顶点(源点)到达另一顶点(终点)的路径可能不止一条,如何找到一条路径使得沿此路径上各边的权值总和(称为路径长度)达到最小。
Dijkstra算法
Dijkstra算法适用于边权为正的情况,是由贪心思想实现的。用于解决单源最短路问题(SSSP)。
Dijkstra朴素算法复杂度为O(n^2),在实际应用中较为稳定。
而堆优化后的dijkstra算法复杂度为O((n+m)logn),稠密图的最短路问题也可有效解决,
伪代码:
清除所有点的标记
设d[0],其他d[i]=inf
循环n次{
在所有为标记结点中,选出d值最小的结点x
给结点x标记
对于从x出发的所有边(x,y),更新d[y]=min{d[y],d[x]+w(x,y)}
}
例子:

声明d[]数组,表示源点v1到其他点的最短路。
则:
| v1 | v2 | v3 | v4 | v5 | v61 | |
|---|---|---|---|---|---|---|
| 1 | 0 | ∞ | ∞ | ∞ | ∞ | ∞ |
| vis | 0 | 0 | 0 | 0 | 0 | 0 |

| v1 | v2 | v3 | v4 | v5 | v6 | |
|---|---|---|---|---|---|---|
| 1 | 0 | ∞ | 10 | ∞ | 30 | 100 |
| vis | 1 | 0 | 0 | 0 | 0 | 0 |
遍历以v1起点的边,继续松弛:即d[to] = min{ d[to] , d[from] + w(from,to) };

| v1 | v2 | v3 | v4 | v5 | v6 | |
|---|---|---|---|---|---|---|
| 2 | 0 | ∞ | 10 | 60 | 30 | 100 |
| vis | 1 | 0 | 1 | 0 | 0 | 0 |
取点v3(因为边(v1,v3)边权最小)同步骤1操作。

| v1 | v2 | v3 | v4 | v5 | v6 | |
|---|---|---|---|---|---|---|
| 3 | 0 | ∞ | 10 | 50 | 30 | 90 |
| vis | 1 | 0 | 1 | 0 | 1 | 0 |
同上操作。

| v1 | v2 | v3 | v4 | v5 | v6 | |
|---|---|---|---|---|---|---|
| 4 | 0 | ∞ | 10 | 50 | 30 | 60 |
| vis | 1 | 0 | 1 | 1 | 1 | 0 |
由于不存在v1到v2的路径,所有d[v2]=∞。
最后得到v1到其他点最短路的大小如上表所示。
堆优化算法模板:
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+3;
const int inf=1e9;
struct Edge{
int from, to, dist;
Edge(int f,int t,int d):
from(f),to(t),dist(d){}
};
struct HeapNode
{
int d, u;
bool operator<(const HeapNode& a){
return d > a.d;
}
HeapNode(int d,int y):d(d),u(u){}
};
struct Dijkstra{
int n,m;
vector<Edge> edges;
vector<int> G[maxn];
bool done[maxn];
int d[maxn];
int p[maxn];
void init(int n){
this->n = n;
for (int i = 0; i < n;i++){
G[i].clear();
}
edges.clear();
}
void addedge(int f,int t,int d){
edges.push_back(Edge(f, t, d));
m = edges.size();
G[f].push_back(m - 1);
}
void dijkstra(int s){
priority_queue<HeapNode> q;
for (int i = 0; i < n;i++)
d[i] = inf;
d[s] = 0;
memset(done, 0, sizeof done);
q.push(HeapNode(0, s));
while(!q.empty()){
HeapNode x = q.top();
q.pop();
int u = x.u;
if(done[u])continue;
done[u] = 1;
for (int i = 0; i < G[u].size();i++){
Edge &e = edges[G[u][i]];
if(d[e.to]>d[u]+e.dist){
d[e.to] = d[u] + e.dist;
p[e.to] = G[u][i];
q.push(HeapNode(d[e.to], e.to));
}
}
}
}
};
题单:
| 来源 | 标题 | 标签 | 难度 |
|---|---|---|---|
| CCF-CSP201703-4 | 地铁修建 | 最小生成树 | ⭐ |
| CCF-CSP201812-4 | 数据中心 | 最小生成树 | ⭐⭐ |
| CCF-CSP201412-4 | 最优灌溉 | 最小生成树 | ⭐⭐ |
| CCF-CSP201712-4 | 行车路线 | 最短路 | ⭐⭐ |
| CCF-CSP201903-5 | 317号子任务 | 最短路 | ⭐⭐⭐ |
二分图匹配
二分图定义
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
简而言之,就是顶点集V可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属于这两个互不相交的子集,两个子集内的顶点不相邻。
以下6个图都是二分图

区别二分图,关键是看点集是否能分成两个独立的点集。
二分图的最大匹配
最大匹配
给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配.
选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)
求二分图最大匹配可以用最大流或者匈牙利算法,以下用例子讲解匈牙利算法。
匈牙利算法
例子:
小明今天和小伙伴们一起去游乐场玩,终于可以坐上梦寐以求的过山车了。过山车的每一排只有两个座位,为了安全起见,规定每个女生必须与一个男生坐一排。但是,每个人都希望与自己认识的人坐在一起。举个例子,1号女生与1号男生相互认识,因此1号女生和1号男生可以坐在一起。另外1号女生与2号男生也相互认识,因此他们也可以坐一起。像这样的关系还有2号女生认识2号和3号男生,3号女生认识1号男生。请问如何安排座位才能让最多的人满意呢?这仅仅是一个例子。实际情况要复杂得多,因为小明的小伙伴们实在是太多了。

对于上面的例子我们很容易找到两种匹配方案:

很显然右边的匹配方案更好,因为有着更多的匹配数
求最大匹配最容易想到的方法是:找出全部的匹配然后输出匹配数最多的。这种方法的时间复杂度是非常高的,那么有没有更好的方法呢?
我们可以这么想,首先从左边的第1号女生开始考虑。先让她与1号男生配对,配对成功后,紧接着考虑2号女生。2号女生可以与2号男生配对,接下来继续考虑3号女生。此时我们发现3号女生只能和1号男生配对,可是1号男生已经配给1号女生了,怎么办?

此时3号女生硬着头皮走到了1号男生面前,貌似1号男生已经看出了3号女生的来意,这个时候1号男生对3号女生说:“我之前已经答应了与1号女生坐一起,你稍等一下,我让1号女生去问问看她能否与其他认识的男生坐一起,如果她找到了别的男生,那我就和你坐一起。”接下来,1号女生便尝试去找别的男生啦
此时1号女生来到了2号男生面前问:“我可以和你坐在一起吗?”2号男生说:“我刚答应和2号女生坐一起,你稍等一下,我让2号女生去问问看她能否与其他认识的男生坐一起,如果她找到了别的男生,那我就和你坐一起。”接下来,2号女生又去尝试找别的男生啦。
此时,2号女生来到了3号男生面前问:“我可以和你坐一起吗?”3号男生说:“我正空着呢,当然可以啦!”此时2号女生回过头对2号男生说:“我和别的人坐在一起啦。”然后2号男生对1号女生说:“现在我可以和你坐在一起啦。”接着,1号女生又对1号男生说:“我找到别的男生啦。”最后1号男生回复了3号女生:“我现在可以和你坐在一起啦。”

匈牙利算法核心
匈牙利算法的核心就是不停的寻找增广路径来扩充匹配集合。
交替路: 从未匹配点出发,依次经过未匹配的边和已匹配的边,即为交替路。
增广路: 如果交替路经过除出发点外的另一个未匹配点,则这条交替路称为增广路。
下图中左边的路都是交替路,也是增广路,其端点都是为匹配点,实线所表示的边都是匹配中的边。如果我们像右边的图那样,将左边路中的实线变成虚线边,将虚线边变成实线边就可以逐步增加匹配中的边(如上述例子的男女通过换人扩大匹配数),从而使得匹配达到最大匹配。匈牙利算法就是基于这种思想。

不难发现这是一个递归的过程,以下是匈牙利算法的实现代码
bool find(int now)
{
for (int i = 0; i < p[now].size();i++)
{
int j = p[now][i];//当前访问的点
if(!vis[j])//如果没有访问过
//j不在增广路径上
{
vis[j] = 1;
if(!match[j]||find(match[j]))//如果没有匹配到或者已经匹配了但可以找到新的匹配
//也可以理解为如果j未匹配或者可以通过j的原匹配点找到增广路径
{
match[j] = now;//匹配到当前的点
return true;
}
}
}
return false;
}
一道模板题
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N=200+10,INF=1e9;
vector<int> p[N];
bool vis[N];
int match[N];
bool find(int now)
{
for (int i = 0; i < p[now].size();i++)
{
int j = p[now][i];
if(!vis[j])
{
vis[j] = 1;
if(!match[j]||find(match[j]))
{
match[j] = now;
return true;
}
}
}
return false;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n;i++)
{
int num;
cin>>num;
for (int j = 1; j <= num;j++)
{
int x;
cin>>x;
p[i].push_back(x);
}
}
int ans = 0;
for (int i = 1; i <= n;i++)
{
memset(vis, 0, sizeof vis);
if(find(i))
ans++;
}
cout << ans;
return 0;
}
二分图的最大权完美匹配
例子:
现在有N男N女,男生和女生每两个人之间有好感度,我们希望把他们两两配对,并且最后希望好感度和最大。

那么该如何选择最优匹配呢?
首先,我们给所有女生一个期望值,就是与她有好感度的男生中最大的好感度,男生的期望值为0。
于是我们给每个人都设定了期望值如下

于是我们开始进行匹配,我们规定匹配方法为,男女两人的期望值加起来要等于两人的好感度之和即可匹配。每一轮匹配,每个男生只会被尝试匹配一次。
第一轮匹配:
女1和男3符合上述匹配规则,于是他们两个匹配成功。
第二轮匹配:
女2和男3也符合匹配规则,但因为男3已经在该轮被匹配过了,同时女2也没有其他的男生进行匹配,因此女2匹配失败
这一轮参与匹配的人有:女1,女2,男3。
为了最大匹配,这两个女生只能降低一下期望值了,该降低多少呢?两个女生都在能选择的其他人中,也就是没参与这轮匹配的男生中,选择一个期望值降低的尽可能小的人。也就是再其他人中选择一个最合适的。比如:女1选择男1,期望值要降低1。 女2选择男1,期望值要降低1。 女2选择男2,期望值要降低2。于是,只要期望值降低1,就有女生可能选择其他人。所以她们的期望值要降低1点。同时,刚才被选的男生此时非常开心,于是他的期望值提高了1点(就是同女生们降低的期望值相同)。于是期望值变成这样(不参与刚才匹配过程的人期望值不变)

于是我们继续为女2进行匹配,此时女2可以与男1匹配,于是女2匹配成功
第三轮匹配:
(女1:选择男3)
(女2:选择男1)
...
继续为女3匹配
女3:此时男3已经与女1匹配,于是女3匹配失败
于是我们需要再一次改变期望值,这次参与匹配的只有女3。
按照之前的匹配原则,我们让女3期望值降低1。

继续为女3匹配
女3选则男3,此时男3已经与女1匹配,于是女1尝试换人,
女1选择男1,此时男1已经与女2匹配,于是女2尝试换人,
由于每个男生每一轮只参与匹配一次,于是女2换人失败,
最终女3匹配失败
这一轮参与的有女1,女2,女2,男1,男3.
再次修改期望值

继续为女3匹配
女1选择男3
女2选择男1
女3选择男3,男3当前与女1匹配,于是女1尝试换人换到了男1,但男1已经与女2匹配,于是女2又尝试换人,此时女2和男2满足匹配规则,于是女2换到了男2。
女3匹配成功
最后结果为:
女1匹配男1
女2匹配男2
女3匹配男3
匹配成功
此时权值最大为9
其本质是一个递归的过程。
以下是KM算法的代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N=300+10,INF=1e9;
int w[N][N];//记录女生对男生的好感度,也就是边的权值
int la[N];//记录每个女生的期望值,也就是左部点的权值
int lb[N];//记录每个男生的期望值,也就是右部点的权值
int va[N];//记录每一轮匹配的女生
int vb[N];//记录每一轮匹配的男生
int match[N];//记录每个男生匹配到的女生,如果没有则为0
int slack[N];//记录每个男生如果能被女生选择最少还需要降低多少的期望值
int n;
bool dfs(int x)//与匈牙利算法类似
{
va[x] = 1;//该名女生参与本轮匹配
for (int y = 1; y <= n;y++)//匹配男生
{
if(vb[y])
continue;//每一轮匹配 每个男生只尝试一次
int need = la[x] + lb[y] - w[x][y];//匹配规则
if(need == 0)//如果符合匹配规则
{
vb[y] = 1;//该名男生参与本轮匹配
if(!match[y]||dfs(match[y]))
//如果该名男生没有被匹配或者可以让与他匹配的男生和其他女生匹配
{
match[y] = x;//那么该女生和男生匹配成功
return true;
}
}
else//不满足匹配规则,我们记录一下slack
{
slack[y] = min(slack[y], need);//记录最少还差多少才有可能匹配
}
}
return false;
}
int KM()
{
memset(match, 0, sizeof match);//初始化,每个男生都还没有匹配女生
memset(lb, 0, sizeof lb);//初始化,每个男生的期望值为0
// 每个女生的初始期望值是与她相连的男生最大的好感度
for (int i = 1; i <= n;i++)
{
la[i] = w[i][1];
for (int j = 2; j <= n;j++)
{
la[i] = max(la[i], w[i][j]);
}
}
//尝试为每一个女生进行匹配
for (int i = 1; i <= n;i++)
{
memset(slack, 0x3f, sizeof slack);//因为要取最小值,所以初始化为无穷大
while(true)
{
//如果能匹配男生就匹配,否则我们需要降低期望值,直到找到男生为止
memset(va, 0, sizeof va);//初始化男生女生均未尝试匹配
memset(vb, 0, sizeof vb);
if(dfs(i))
break;//如果匹配成功直接退出
//否则需要找到要降低的最小的期望值
int d = INF;
for (int j = 1; j <= n;j++)
{
if(!vb[j])//如果没有参与本轮匹配就找到需要降低的最小的期望值
d = min(d, slack[j]);
}
for (int j = 1; j <= n;j++)
{
//所有参与本轮匹配的女生和男生分别降低和增加期望值
if(va[j])
la[j] -= d;
if(vb[j])
lb[j] += d;
}
}
}
int res = 0;
//求出所有匹配的好感度之和
for (int i = 1; i <= n;i++)
{
res += w[match[i]][i];
}
return res;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
while(cin>>n)
{
for (int i = 1; i <= n;i++)
{
for (int j = 1; j <= n;j++)
{
cin>>w[i][j];
}
}
cout << KM() << '\n';
}
return 0;
}
tarjan算法
简介
Tarjan算法是基于对图深度优先搜索的算法。算法复杂度为O(n),主要用于处理强连通分量问题。
但可以依据tarjan算法的思想来解决 双连通分量,割点和桥等问题。是不是很🐂🍺,但是很可惜,今天不讲(氵,咳咳)。
本文将介绍tarjan算法处理强连通分量的原理以及缩点操作,并给通过tarjan算法求出无向图的割点和桥简略方法以及代码(当作干货,不用谢(氵,咳咳))。
强连通分量:简单地讲,就是任意两点都可互相到达的极大子图。
例如:图中有结点2,3,4构成的环(显然一个简单环一定是强连通分量)。

DFS遍历
在介绍tarjan算法求强连通分量前,先带大家认识一种DFS遍历所有边和点的方式:
还记得树的后序遍历嘛,接下来的DFS与其类似。
我们先递归所能遍历的点,再访问当前结点,并且已经被遍历到的点不会在接下来的DFS中被访问。
举个🌰(栗子):如下图:

我们以1点为起始点开始进行DFS:
进行搜索
DFS(1):不过在访问结点1前,我们先DFS(2);同时标记结点1以及被访问过了。
DFS(2):同上,我们对结点2进行标记,我们先对它的相邻结点3,6进行DFS;之后再访问2。
DFS(3):同上,对结点3进行标记,对它的相邻结点4进行DFS;再访问3。
DFS(4):对4进行标记,DFS(5);再访问5。
DFS(5):对5进行标记,由于5出度为0,即无边可进行DFS,这直接访问5,之后一直回溯上去。
DFS(6):对6进行标记,DFS(7),之后再访问6。
DFS(7):对7进行标记,由于2早以及被访问过了,所有不去DFS(2),故直接访问7。之后一直回溯上去。
这个DFS过程如图所示:

tarjan求强连通分量实现过程
接下来的tarjan算法也需要上述类似的DFS。
不过,首先我们需先介绍一个概念:
时间戳:在这里,我们标记每个结点的遍历次序,而这个遍历次序为时间戳。
然后接下来我们用一个二元组(x,y)来表示一个点的信息:
- x:在DFS中所遍历到的时间戳。(下面或用dfn表示)
- y:在DFS中通过指向下一有向边的结点更小时间戳(如果没有,这个值就为x)。(下面或用low表示)
如图中一个DFS过程:

接下来,我们通过上述的DFS搜索方式对这些结点进行赋予他们的时间戳:先从结点1一直递归到5:

然后接下来开始访问5结点。由于存在(5,3)这有向边:且结点3的时间戳dfn(3)小于结点5的可达到时间戳low(5),故更新5的可达到时间戳,如图:

然后回溯访问结点4,发现结点5的可达时间戳小于结点4的可达时间戳,则更新4的可达时间戳(意思是可通过结点5到达时间戳更小的点),如图:

这时候回溯到结点3,这时无法改变结点3的可达时间戳:即3的当前时间戳dfn(3) = 可达时间戳low(3) 。这时候,我们注意到结点3,4,5构成了一个强连通分量,显然,我们很容易想到当一个结点u:low(u)<dfn(u)时:说明u结点可访问到更早访问的结点。
我们对结点6,7在DFS过程中做同样的操作:


最后我们发现对于回溯过程从结点7->结点6->结点2中,只有low(2)=dfn(2),因为结点7和结点6的可达时间戳low与2的当前时间戳相等,所以6和7存在一条路径通向2,即2,6,7构成环。
于是我们可以简单的得到一个结论,如果一个点的dfn = low,那么它的当前时间戳是强连通分量中的点最早可达的时间戳。这时候大家可能知道该怎么找强连通分量了吧。
这时候,我们准备一个栈这一数据结构来求出所用强连通分量:
在遍历过程中,将点依次入栈:

接着进行回溯:
直至发现一个点满足 dfn=low,在这张图时,为结点3。
元素依次出栈,直到出栈元素为3,这时(3,4,5)构成的子图为强连通分量。
如图:

同理:回溯到2时,对6,7进行DFS,6、7依次入栈:

最后从结点7开始回溯:直到结点2,发现2结点的dfn和low是相等的,故开始出栈元素7、6,直到2,停止,这时又一个强连通分量找了,及(2,6,7)所构成的强连通分量。
最后由于结点1的强连通分量low=dfn,所以1也出栈,被视作为一个强连通分量。
至此,全部强连通分量以及求得完毕:如图:

下面给出求强连通分量的(两份)完整模板代码(分别使用链式前向星和邻接表建图)
链式前向星:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e4 + 3;//最大点数
const int maxm = 2e4 + 3;//最大边数
struct Edge{
int _next;
int to;
}edge[2*maxm];
int head[2*maxn];
int cnt;
void add(int u,int v){
edge[cnt].to = v;
edge[cnt]._next = head[u];
head[u] = cnt++;
}//链式前向星建图。
int dfs_clock;
int dfn[maxn], low[maxn];
int sccno[maxn], scc_cnt;
vector<int> scc[maxn];
stack<int> s;
void tarjan(int u,int fa){
pre[u] = low[u] = ++dfs_clock;
s.push(u);
for (int i = head[u]; i;i=edge[i]._next){
int v = edge[i].to;//边(u,v)
if(!dfn[v]){
tarjan(v,u);
low[u] = min(low[u], low[v]);
}
else if (!sccno[v]){//如果未对sccno[v]编号,即v与u同属于一个scc
low[u] = min(low[u], dfn[v]);
}
}
if(low[u]==dfn[u]){
scc_cnt++;//scc个数
scc[scc_cnt].clear();
for (;;){
int x = s.top();
s.pop();//并将其标记为同一个scc。
sccno[x] = scc_cnt;
scc[scc_cnt].push_back(x);
if(x==u)
break;//退出循环
}
}
}
void find_scc(int n){
for (int i = 1; i <= n;i++){
if(!dfn[i]){
tarjan(i,-1);
}
}
}
vector邻接表:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e4 + 3;
vector<int> G[maxn];
int dfs_clock;
int dfn[maxn], low[maxn];
int sccno[maxn], scc_cnt;
vector<int> scc[maxn];
stack<int> s;
void tarjan(int u,int fa){
pre[u] = low[u] = ++dfs_clock;
s.push(u);
for (int i = 0; i < G[u].size();i++){
int v = G[u][i];
if (!dfn[v]){
tarjan(v, u);
low[u] = min(low[v], low[u]);
}
else if(!sccno[v]){
low[u] = min(low[u], dfn[v]);
}
}
if(low[u]==dfn[u]){
scc_cnt++;
scc[scc_cnt].clear();
for (;;){
int x = s.top();
s.pop();
sccno[x] = scc_cnt;
scc[scc_cnt].push_back(x);
if(x==u)
break;
}
}
}
void find_scc(int n){
for (int i = 1; i <= n;i++){
if(!dfn[i]){
tarjan(i,-1);
}
}
}
缩点操作:
将一个强连通分量缩成一个点。
例如:

vector<int> new_G[maxn];
for(int i=1;i<=n;i++){
int u=sccno[i];
for(int j=0;j<G[i].size();i++){
int v=sccno[G[i][j]];
if(u!=v)//在同一个强连量的不考虑。
{
new_G[u].push_back(v);
}
}
}
干货:桥与割点
1.桥:在连通的无向图中,当一条边被去掉时,此时图不在连通,则这条边为桥;
显然如果在无向图中,对于边(u,v)如果 dfn(u) < low(v) ,即v点无法回溯到u点前,则只要破坏 (u,v)这条边,这连通性会被破坏。
int n;
vector<int> G[maxn];
int low[maxn], dfn[maxn];
int dfs_clock = 0;
struct edge{
int x, y;
edge(int x,int y):x(x),y(y){}
};
int cnt = 0;
vector<edge> ans;
int tarjan(int u,int fa){
int lowu = pre[u] = ++dfs_clock;
for (int i = 0; i < G[u].size();i++){
int v = G[u][i];
if(!dfn[v]){
int lowv = tarjan(v, u);
lowu = min(lowv, lowu);
if(lowv>dfn[u]){
int a = u, b = v;
if(a>b)
swap(a, b);
bridge.push_back(edge(a, b));
}
}
else if(v!=fa&&dfn[v]<dfn[u]){
lowu = min(lowu, pre[v]);
}
}
low[u] = lowu;
return lowu;
}
2.割点:在连通的无向图中,当图中某一点被去掉时,此时图不再连通,则该点为割点。
如果对于无向图中,有一条边(u,v)满足 low(v) >= dfn(u) ,则v为割点。
vector<int> G[maxn];
int dfn[maxn],iscut[maxn],low[maxn];
int dfs_clock=0;
int dfs_low(int u,int fa){
int lowu,child=0;
lowu=pre[u]=++dfs_clock;
for(int i=0;i<G[u].size();i++){
int v=G[u][i];
if(!dfn[v]){
child++;
int lowv=dfs_low(v,u);
lowu=min(lowv,lowu);//if v can go there ,the u alse can go there.
if(lowv>=pre[u])
{
iscut[u]=1;
}
}
else if(pre[v]<dfn[u]&&v!=fa){
lowu=min(lowu,dfn[v]);//rejust_the_reverse_edge
}
}
if(fa<0&&child==1)iscut[u]=0;//need to judge the root node specially
low[u]=lowu;
//cout<<u<<' '<<lowu<<' '<<pre[u]<<endl;
return lowu;
}
题单:
| 来源 | 标题 | 标签 | 难度 |
|---|---|---|---|
| CCF-CSP201509-4 | 高速公路 | tarjan算法,强连通分量 | ⭐⭐ |
| (⭐)luogu p3387 | 【模板】缩点 | tarjan算法、缩点,拓扑排序、dp | ⭐⭐ |
| HDU4635 | Strongly connected | tarjan算法,缩点 | ⭐⭐ |
| poj1236 | Network of Schools | tarjan算法,缩点 | ⭐⭐⭐ |
| UVA12167 | Proving Equivalences | tarjan算法,强连通分量缩点,数学 | ⭐⭐ |
| POJ3352 | Road Construction | tarjan算法,缩点,边双连通分量 | ⭐⭐ |
| Luogu p2515 | 软件安装 | tarjan算法,强连通分量缩点,dp(树上背包) | ⭐⭐⭐ |
| (⭐)luogu p3388 | 【模板】割点(割顶) | tarjan算法、割点 | ⭐ |
| POJ1144 | Network | tarjan算法、割点 | ⭐⭐(题目不难,但是输入很阴间) |
| UVA 796 | Critical Links(模板题,注意输入输出) | tarjan算法、桥 | ⭐⭐ |
| luogu p3379 | 【模板】最近公共祖先(LCA) | 最近公共祖先 | ⭐⭐ |
| POJ2942 | Knights of the Round Table | tarjan算法,点双连通分量,二分图 | ⭐⭐⭐⭐ |
| Luogu p5058 | 嗅探器 | tarjan算法,割点 | ⭐⭐⭐ |
| Luogu p3225 | 矿场搭建 | DFS,tarjan,割点,点双连通分量 | ⭐⭐⭐ |
| UVA11324 | The Largest Clique | tarjan算法,强连通分量缩点 | ⭐⭐⭐ |
| Luogu p1407 | 稳定婚姻 | tarjan算法,缩点,二分图 | ⭐⭐⭐ |
| Luogu p3386 | 【模板】二分图最大匹配 | 匈牙利算法,二分图最大匹配 | ⭐ |
| Luogu p1894 | [USACO4.2]完美的牛栏The Perfect Stall | 匈牙利算法,二分图最大匹配 | ⭐ |
| HDU2063 | 过山车 | 匈牙利算法,二分图最大匹配 | ⭐ |
| Luogu p1640 | [SCOI2010] 连续攻击游戏 | 匈牙利算法,二分图最大匹配 | ⭐⭐ |
| Luogu p2071 | 座位安排 | 匈牙利算法,二分图最大匹配 | ⭐⭐ |
| Luogu p2756 | 飞行员配对方案问题 | 匈牙利算法,二分图最大匹配 | ⭐⭐ |
| Acwing373 | 車的放置 | 匈牙利算法,二分图最大匹配 | ⭐⭐⭐ |
| Acwing372 | 棋盘覆盖 | 匈牙利算法,二分图最大匹配 | ⭐⭐⭐ |
| Acwing374 | 导弹防御塔 | 匈牙利算法,二分图最大匹配,二分答案 | ⭐⭐⭐⭐ |
| Acwing406 | 放置机器人 | 匈牙利算法,二分图最大匹配 | ⭐⭐⭐⭐ |
| HDU2255 | 奔小康赚大钱 | KM算法,二分图最大权完美匹配 | ⭐⭐⭐ |
| HDU1533 | Going Home | KM算法,二分图最大权完美匹配 | ⭐⭐⭐ |
| Luogu p6577 | 【模板】二分图最大权完美匹配 | KM算法(BFS),二分图最大权完美匹配 | ⭐⭐⭐⭐ |
引用资料:
二分图的最大匹配:
《啊哈!算法》
二分图的最大权完美匹配(KM算法):
https://www.cnblogs.com/wenruo/articles/5264235.html
并查集:
https://blog.csdn.net/qq_54773252/article/details/122721128?ops_request_misc=&request_id=&biz_id=102&utm_term=并查集&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduweb~default-9-122721128.142v40control,185v2tag_show&spm=1018.2226.3001.4187
最小生成树(prim):
https://blog.csdn.net/qq_62213124/article/details/121597780?ops_request_misc=&request_id=&biz_id=102&utm_term=prim&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduweb~default-1-121597780.142v40control,185v2tag_show&spm=1018.2226.3001.4187


 浙公网安备 33010602011771号
浙公网安备 33010602011771号