博弈论算法总结
正在完善!
何为博弈论
博弈论 ,是经济学的一个分支,主要研究具有竞争或对抗性质的对象,在一定规则下产生的各种行为。博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。
先来看一道小学就接触过的思维题
你和好基友在玩一个取石子游戏。面前有30颗石子,每次只能取一颗或两颗,你先取,取完的人为胜,问你是否有必胜策略
Q:什么?有必胜策略?能否胜利不应该随着我们选择而改变吗?
A:确实。但如果我们足够聪明呢?每次都做最优的选择,把取胜之路留给自己
Q:我一点也不聪明,那该如何做呢?
先从简单入手,
假如只有一个或两个石子,无疑先手必胜
只有三个石子,无疑先手必输
(我们约定先手必败状态为必败状态,先手必胜状态为必胜状态)
这就是我们的终止状态,即无论怎么拿,都会回到这几个状态
因为我们想赢,所以我们要让自己处于必胜状态,即剩下一个或两个石子的时候,我们是先手。不难发现,我们也许不能使自己处于必胜态,但我们可以让对方处于必败态。即剩下三个石子的时候,我们是后手。
不难发现,只要是三的倍数就一定是必败状态,否则就是必胜状态。
证明:
假设不是三的倍数,我们使它成为三的倍数,此时我们是后手。对方如果拿一个,我们就拿两个;如果拿两个,我们就拿一个。所以我们那完后剩下的一定永远是三的倍数,所以只剩下三个石子的时候我们一定是后手,此时对手必输,也就是我们必胜。
假设是三的倍数,因为两个人都足够聪明,所以对方一定会使我们永远处于三的倍数中。所以我们必败。
所以只要判断是不是三的倍数,就可以确定我们是否必胜了
至此,小学时代遗留的问题已经解决了可以拿去欺负同学,(这也是博弈论最基础的问题,Nim游戏)
可以说,你已经学会博弈论了
下面我主要讲一些关于算法比赛中用到的博弈类型:
首先你要理解必胜状态和必败状态:
对下先手来说,
一个状态是必败状态当且仅当它的所有后继都是必败状态。
一个状态是必胜状态当且仅当它至少有一个后继是必败状态。
就是说,博弈者,一旦捉住了胜利的把柄,必然最后胜利。
博弈中常常用到的:
两个数,不用中间变量实现交换。
a b;
a = a^b;
b = a^b;
a = a^b;
博弈图和状态
把每个可到达的状态都看做结点,每次做出决策都是从旧的状态转移到新的状态,也就是在两个状态结点间连一条有向边。如果把所有状态转移都画出来,我们就得到了一张博弈图
就像这样
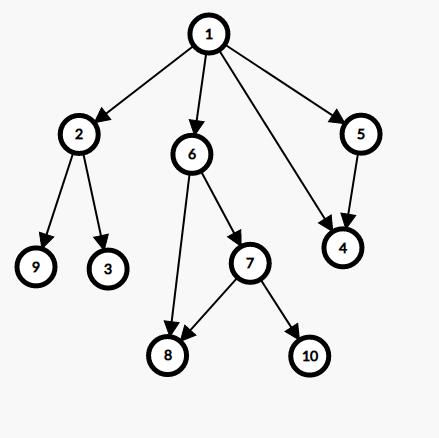
大多数博弈图会是一个DAG,否则游戏不可能结束
三个基本定理
- 定理一:没有后继状态的状态是必败状态
- 定理二:一个状态是必胜状态 当且仅当 存在至少一个必败状态为它的后继状态。
- 定理三:一个状态是必败状态 当且仅当 它的所有后继状态均为必胜状态。
对于定理一,游戏进行不下去了,即这个玩家没有可操作的了,那么这个玩家就输掉了游戏
对于定理二,如果该状态至少有一个后继状态为必败状态,那么玩家可以通过操作到该必败状态;此时对手的状态为必败状态,即对手必定是失败的,而相反地,自己就获得了胜利。
对于定理三,如果不存在一个后继状态为必败状态,那么无论如何,玩家只能操作到必胜状态;此时对手的状态为必胜状态——对手必定是胜利的,自己就输掉了游戏。
SG函数
有向图游戏是一个经典的博弈游戏——实际上,大部分的公平组合游戏都可以转换为有向图游戏。
在一个有向无环图中,只有一个起点,上面有一个棋子,两个玩家轮流沿着有向边推动棋子,不能走的玩家判负。
定义 mex 函数的值为不属于集合 S 中的最小非负整数,即:
mex(S) = min{x} ( x ∉ S , x ∈ N )
例如 mex({0,1,3,4})=1,mex({1,2})=0,mex({})=0
对于状态 x 和它的所有 k 个后继状态 y1,y2,...,yk,定义 SG 函数:
SG(x)=mex{SG(y1),SG(y2),...,SG(yk)}
SG定理:
而对于由 n 个有向图游戏组成的组合游戏,设它们的起点分别为 s1,s2,...,sn ,则有定理: 当且仅当
SG(s1)⊕SG(s2)⊕...⊕SG(sn)≠0 时,这个游戏是先手必胜的。
还是拿原来那个图开刀
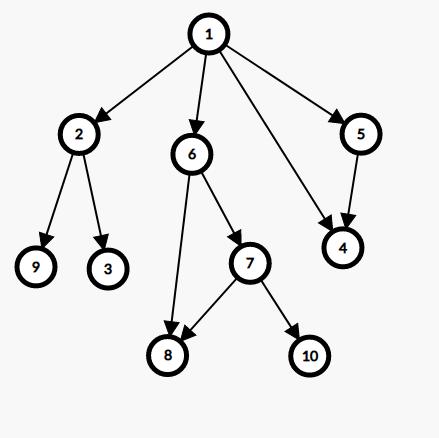
用 SG[] 数组来存所有结点的 SG 函数值因为 9,3,8,10,4 这几个点都没有后继状态,所以它们 SG 值均为 0,同理推出 2,7,5这个点的 SG 值为 1,而
SG[6]=mex(SG[7],SG[8])=2
SG[1]=mex(SG[2],SG[5],SG[6],SG[4])=3
把 Nim游戏 转化为有向图游戏
我们可以将一个有 x 个物品的堆视为节点 x ,拿掉若干个石子后剩下 y个,则当且仅当 0<y<x 时,节点 x 可以到达 y 。
那么,由 n 个堆组成的 Nim 游戏,就可以视为 n 个有向图游戏了。根据上面的推论,可以得出 SG(x)=x 。
再根据 SG 定理,就可以得出 Nim 和的结论了。
博弈论DP
不得不说,博弈论DP就是个神仙做法,能用博弈论DP做的都是神仙题!
并没有什么固定的做法,但基本原理还是照着那三个定理来。能用DP的一般是因为想不出来如何用 SG 定理。状态的设计都比较神仙,主要是根据题目要求来设计。
习题
P2197 【模板】Nim 游戏
题目本意是给出 n 堆石子,轮流在其中一堆去任意个,谁不能去谁就输。
思路:证明所有石子异或和为0则先手必输
证明:
-
反正最终情况就是每堆都为0,先手必输,所以我们考虑怎么把情况转换到这里。
-
如果异或和的最高位为i,则有一堆石子第i为为1(不然怎么会有i位)
-
设A1就为那堆石子,其他堆石子异或和设为x,总异或和设为k,则 A1 xor x=k,把A1变成A1 xor k,那么后手面对的则是(A1 xor k)xor x=0,
举个例子:11001 xor 11100=101,则有(11001 xor 101)xor 11100=0
-
如果现在的异或和已经为0了(不为最终情况),那么怎么转换异或和都不能为0
-
好,我们根据3 4点得出:如果先手异或和不为0,可以一步让后手的情况为异或和为0;如果先手异或和为0,那么后手异或和就不为0
-
终于开始进行游戏了,如果现在先手面对的情况异或和不为0,则一直让后手异或和为0,最后面对最终情况,后手输,则先手赢;如果先手面对的情况异或和为0,后手则赢
代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
int t;
cin>>t;
while(t--){
int s=0;
int n;
cin>>n;
for(int i=1;i<=n;i++){
int a;
cin>>a;
s^=a;
}
if(s==0)cout<<"No"<<endl;
else cout<<"Yes"<<endl;
}
return 0;
}
P1247 取火柴游戏
这个游戏的SG值就是各堆数量的异或和,当SG为0时先手必败,否则先手就要把SG变为0
先检验SG值,如果是0输出lose,否则我们按照以下原则行动
有n个数的异或值不为0 现在要减少一个数使异或值为0
假设n个数:a1 ,a2,a3...an
a1 ^ a2 ^ a3 ^ .. ^ an=k
那么我们可以对一个数进行操作,假设这个数是a1,设a1 ^ k = a',a' ^ a2 ^ a3 ^ ... ^ an = a1 ^ a2 ^ a3 ^ ... ^ an ^ k = k ^ k = 0;
所以我们只需要从头到尾检验每个数异或k的值是否比它小(因为是要减少),遇到小的直接输出ai-ai ^ k即可
代码如下:
#include<bits/stdc++.h>
using namespace std;
int k,n[500010];
int main(){
cin>>k;
int x=0;
for(int i=1;i<=k;i++){
cin>>n[i];
x^=n[i];
}
if(!x){
cout<<"lose"<<endl;
return 0;
}
for(int i=1;i<=k;i++){
if((n[i]^x)>=n[i])continue;
cout<<n[i]-(n[i]^x)<<" "<<i<<endl;
n[i]=n[i]^x;
break;
}
for(int i=1;i<=k;i++)cout<<n[i]<<" ";
return 0;
}
P4101 [HEOI2014] 人人尽说江南好
首先,合并次数为奇数先手必胜,偶数后手必胜,那么两个人都会尽可能向着自己想要的方向去发展(即拉到总合并次数为奇数/偶数)
当n ≤ m时,这种情况最后肯定能合成一堆,我们称这个较大的堆为【大堆】。
假如现在轮到先手操作,先手还没动,这个时候最长合并次数为偶数次,那么先手有两种可能性,把后面一个堆丢进大堆里面,这样后手再丢一个小堆进去,或者把后面两个堆合成一个,那么后手就可以把这个合成的直接丢进去。
无论怎么做,后手都能保证每轮完了之后,大堆的石子会增加两个,那么合并次数也会-2,一直保持为偶数。直到最后先手合无可合。
因此就可以保证剩下的合并次数为原始奇/偶,同时这种方式也会把局数拉到最多。
想办法弄到对自己有利
如果拉到最长的操作次数我们必胜的话,那么不管对面怎么操作,我们都能用上述方法拉回来
同样如果最长的操作是对面必胜,不管我们怎么合并,对面也能用上述方法拉回来
以及
我们已经发现最长的情况我们必胜,无论对手怎么操作我们都能拖到最长,我们必胜
对手发现最长他必胜,无论我们怎么操作,他也肯定能往下拖。
所以对最长必胜的那一方来说,一直拖到最长就是最优策略
而我们已经分析了必胜的那一方总是能拖下去
即这是一种必然取胜的方法,且如果对手不按套路出牌我们也能拖回来。
因此最终答案就是最长能拖到的次数,如果为奇先手胜,如果为偶后手胜。
最长次数
在n<=m的情况下可以轻松判断出是n-1;
若n>m,则最后最大合并后堆数一定是{m,m,m,m,n%m}; (因为如果是形如{m,m,m,m-x,m-x}的形式,不好算,我觉得其实是没什么不一样的,可能仅仅只是不好算吧)
因此 ans=(n/m)×(m-1)+n%m?n%m-1:0;
代码如下:
#include<bits/stdc++.h>
using namespace std;
int T;
long long n,m;
int main(){
cin>>T;
while(T--){
cin>>n>>m;
long long ans=(n/m)*(m-1)+((n%m)?(n%m-1):0);
if(ans&1)cout<<0<<endl;
else cout<<1<<endl;
}
return 0;
}
P3480 [POI2009] KAM-Pebbles
设a[i]表示第i堆石子的个数,c[i]表示a[i]-a[i-1],则我们每堆可以拿的石子数即为c[i]。当我们在第i堆拿了x个时,c[i]变成了c[i]-x,c[i+1]变成了c[i+1]+x,相当于我们把第i堆中可拿的石子转移到了i+1堆,由此我们可以把此题转化为一道反着的阶梯nim游戏。
下面简单讲解一下阶梯nim,如果不懂的话可以去网上搜一下。
阶梯nim是指,有n堆石子,每次我们可以从第i堆的石子中拿走一部分放到第i-1堆中,或者把第1堆中的石子拿走一部分,无法操作的人算输。先说结论:阶梯nim的游戏结果与只看奇数堆的石子数的普通nim结果相同。
假设我先手,那么我可以按照必胜策略把奇数堆中的石子转移到偶数堆,当对方拿的时候我们分情况讨论:
-
对方拿奇数堆中的石子到偶数堆,相当于进行对于奇数堆的普通nim,我们继续按照必胜策略拿奇数堆中的石子;
-
对方把偶数堆的石子拿到奇数堆,则我们可以把这部分石子继续向下拿,对于奇数堆相当于局势没有变动。
代码如下:
#include<bits/stdc++.h>
using namespace std;
int T;
const int N=1e3+10;
int a[N];
int b[N];
int n;
int main(){
cin>>T;
while(T--){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=a[i]-a[i-1];
}
int ans=0;
for(int i=n;i>=1;i-=2){
ans^=b[i];
}
if(ans)cout<<"TAK"<<endl;
else cout<<"NIE"<<endl;
}
return 0;
}
最后来一道黑体吧!
P3235 [HNOI2014] 江南乐
我们在整体上使用 SG 函数的性质。
我们单独求出每一个石子堆的 SG 函数值,最后求异或和即可。
我们可以写记忆化搜索,因为有用的 SG 函数项不多,这样节省时间。
问题中的操作将石子分成了很多石子,不好处理。
但是,种类只有两类,同样的石子堆的 SG 函数值肯定相同。
分成多个石子堆后,注意到有很多相同的,根据 SG 函数的性质,可以异或抵消。
所以其实相同的石子堆 SG 函数值异或之后抵消了。
对于操作后产生的每种石子堆,我们可以根据石子数量奇偶性质思考讨论。
如果是奇数,那最后还有一个没抵消。
如果是偶数,那么全部抵消掉了。
也就是看起来很多堆石子,其实到头来,每个种类最多一个最少没有。
这时候还不够,需要剪枝。
最后要用到分块。
代码如下:
#include<bits/stdc++.h>
using namespace std;
int T,F;
int n;
const int N=110;
const int M=1e5+5;
int sg[M];
int dfs(int x){
if(~sg[x])return sg[x];
if(x<F)return sg[x]=0;
int vis[M];
memset(vis,0,sizeof vis);
for(int i=2;i<=x;i++){
int sum=0;
if((x+i-1)/i<F){
vis[sum]=1;
break;
}
if(x%i&1)sum^=dfs(x/i+1);
if((i-x%i)&1)sum^=dfs(x/i);
vis[sum]=1;
}
for(int i=0;i<=100;i++){
if(!vis[i]){
sg[x]=i;
return i;
}
}
}
int main(){
cin>>T>>F;
memset(sg,-1,sizeof sg);
while(T--){
cin>>n;
int ans=0;
for(int i=1;i<=n;i++){
int x;
scanf("%lld",&x);
ans^=dfs(x);
}
if(!ans)printf("0 ");
else printf("1 ");
}
return 0;
}




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· DeepSeek 解答了困扰我五年的技术问题。时代确实变了!
· 本地部署DeepSeek后,没有好看的交互界面怎么行!
· 趁着过年的时候手搓了一个低代码框架
· 推荐一个DeepSeek 大模型的免费 API 项目!兼容OpenAI接口!