机器学习实战学习笔记(二)-KNN算法(1)-KNN的最基本实现
机器学习实战学习笔记(2)-KNN算法(1)-KNN的最基本实现
k-近邻算法
k-近邻算法概述
简单地说,k-近邻算法采用测量不同特征值之间的距离方法进行分类。
k-近邻算法特点
优点:精度高、对异常值不敏感、无数据输入假定。
缺点:计算复杂度高、空间复杂度高。
适用数据范围:数值型和标称型。
k-近邻算法原理
例子
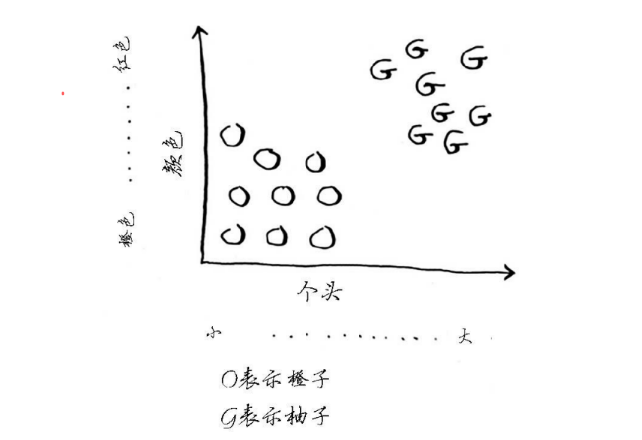
现在有一个神秘的水果,现在我们想知道它是橙子还是柚子。通常我们知道,柚子通常比橙子更大、更红。
1.现在按照以水果的个头属性为横坐标,以水果的颜色属性为纵坐标,将已知的一些橘子和柚子的数据画到平面上
2.将未知神秘水果按照它的属性信息绘制到坐标图上
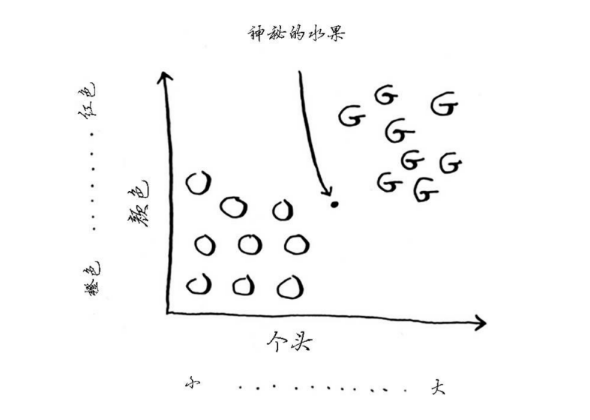
3.如果判断这个水果是橙子还是柚子呢?一种办法是看它的邻居。来看看离它最近的三个邻居。

4.在这三个邻居中,橙子比柚子多,因此这个水果很可能是橙子
注解:
- 判断神秘水果是什么水果主要看,离它距离最近的三个水果中,哪一类水果多,那类水果多它就是什么水果。如果拓展一下,看离它距离最近的K个水果中,哪类水果多,那么就是K近邻啦,K通常是小于等于20的整数
- 核心思想:近朱者赤,近墨者黑,向了解你是什么人,只需要看离你平时最近的K个人中,那类人多,你就是哪类人
k-近邻算法的一般流程
- 收集数据:可以使用任何方法。
- 准备数据:距离计算所需要的数值,最好是结构化的数据格式。
- 分析数据:可以使用任何方法。
- 训练算法:此步骤不适用于k-近邻算法。
- 测试算法:计算错误率。.
- 使用算法:首先需要输入样本数据和结构化的输出结果,然后运行h-近邻算法判定输入数据分别属于哪个分类,最后应用对计算出的分类执行后续的处理。
k-近邻算法实现
算法实现步骤
对未知类别属性的数据集中的每个点依次执行以下操作:
(1)计算已知类别数据集中的点与当前点之间的距离;
(2)按照距离递增次序排序;
(3)选取与当前点距离最小的k个点;
(4)确定前k个点所在类别的出现频率;
(5)返回前k个点出现频率最高的类别作为当前点的预测分类。
算法代码
1.生成数据
import numpy as np
import operator
import matplotlib.pyplot as plt
#创建数据集
def creatDataSet():
group=np.array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
labels=['A','A','B','B']
return group,labels
#画图
def creatGraph():
groupData,_=creatDataSet()
x=[item[0] for item in groupData]
y=[item[1] for item in groupData]
plt.scatter(x,y,alpha=0.6)
plt.show()
if __name__ == "__main__":
creatGraph()
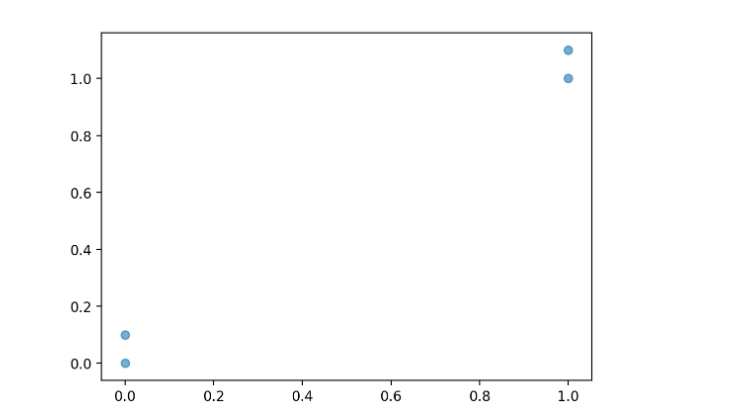
2.knn算法
因为用到了np.tile函数,所以说明一下:
>>> import numpy as np
>>> inX=[0,0]
>>> np.tile(inX,(4,1))#显然,原来的列都没变,赋值到了四行
array([[0, 0],
[0, 0],
[0, 0],
[0, 0]])
>>> np.tile(inX,(4,2))#列方向复制了两次,行方向复制了4次
array([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]])
>>> np.tile(inX,(2,1))#同理
array([[0, 0],
[0, 0]])
knn代码
#K近邻算法
#inX是输入的数据
#dataSet是训练的数据
#labels是标签,类别
#k是周围邻居的数量
#返回预测的类别
def knnClassify(inX,dataSet,labels,k):
#计算欧式距离
dataSetSize=dataSet.shape[0]#shape是(4,2),要获取点的数量显然是shape[0]
diffMat=np.tile(inX,(dataSetSize,1))-dataSet
'''
np.tile(inX,(dataSetSize,1))=[[0,0],[0,0],[0,0],[0,0]]
dataSet=[[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]]
np.tile-dataSet=[[-1.0,-1.1],[-1.0,-1.0],[0,0],[0,-0.1]]
即([x1-x0,y1-y0],[x2-x0,y2-x0],[x3-x0,y3-y0],[x4-x0,y4-y0])
'''
sqdiffMat=diffMat**2
#([(x1-x0)**2,(y1-y0)**2],[(x2-x0)**2,(y2-x0)**2],[(x3-x0)**2,(y3-y0)**2],[(x4-x0)**2,(y4-y0)**2])
sqDistances=sqdiffMat.sum(axis=1)
#([(x1-x0)**2+y1-y0)**2],[(x2-x0)**2+(y2-x0)**2],[(x3-x0)**2+(y3-y0)**2],[(x4-x0)**2+(y4-y0)**2])
# print(sqDistances)
distances=sqDistances**0.5
#([(x1-x0)**2+(y1-y0)**2]**(0.5),[(x2-x0)**2+(y2-x0)**2]**(0.5),[(x3-x0)**2+(y3-y0)**2]**(0.5),[(x4-x0)**2+(y4-y0)**2])**(0.5)
sortedDistIndicies=distances.argsort()#按照数值大小对下标排序,[2 3 1 0]
classCount={}
#选择距离最小的k个点
for i in range(k):
votIlabel=labels[sortedDistIndicies[i]]#获取最近的K个邻居的距离,对应的目标值
# print(votIlabel)
classCount[votIlabel]=classCount.get(votIlabel,0)+1#get(key,default)当key不存在时候默认值是default
sortedClassCount = sorted(classCount.items(), key=op.itemgetter(1), reverse=True)
# [('B', 2), ('A', 1)]
return sortedClassCount[0][0]#返回与其最近的k个邻居中,出现最多的次数
3.全部源代码
import numpy as np
import operator as op
import matplotlib.pyplot as plt
#创建数据集
def creatDataSet():
group=np.array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
labels=['A','A','B','B']
return group,labels
#画图
def creatGraph():
groupData,_=creatDataSet()
x=[item[0] for item in groupData]
y=[item[1] for item in groupData]
plt.scatter(x,y,alpha=0.6)
plt.show()
#K近邻算法
#inX是输入的数据
#dataSet是训练的数据
#labels是标签,类别
#k是周围邻居的数量
#返回预测的类别
def knnClassify(inX,dataSet,labels,k):
#计算欧式距离
dataSetSize=dataSet.shape[0]#shape是(4,2),要获取点的数量显然是shape[0]
diffMat=np.tile(inX,(dataSetSize,1))-dataSet
'''
np.tile(inX,(dataSetSize,1))=[[0,0],[0,0],[0,0],[0,0]]
dataSet=[[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]]
np.tile-dataSet=[[-1.0,-1.1],[-1.0,-1.0],[0,0],[0,-0.1]]
即([x1-x0,y1-y0],[x2-x0,y2-x0],[x3-x0,y3-y0],[x4-x0,y4-y0])
'''
sqdiffMat=diffMat**2
#([(x1-x0)**2,(y1-y0)**2],[(x2-x0)**2,(y2-x0)**2],[(x3-x0)**2,(y3-y0)**2],[(x4-x0)**2,(y4-y0)**2])
sqDistances=sqdiffMat.sum(axis=1)
#([(x1-x0)**2+y1-y0)**2],[(x2-x0)**2+(y2-x0)**2],[(x3-x0)**2+(y3-y0)**2],[(x4-x0)**2+(y4-y0)**2])
# print(sqDistances)
distances=sqDistances**0.5
#([(x1-x0)**2+(y1-y0)**2]**(0.5),[(x2-x0)**2+(y2-x0)**2]**(0.5),[(x3-x0)**2+(y3-y0)**2]**(0.5),[(x4-x0)**2+(y4-y0)**2])**(0.5)
sortedDistIndicies=distances.argsort()#按照数值大小对下标排序,[2 3 1 0]
classCount={}
#选择距离最小的k个点
for i in range(k):
votIlabel=labels[sortedDistIndicies[i]]#获取最近的K个邻居的距离,对应的目标值
# print(votIlabel)
classCount[votIlabel]=classCount.get(votIlabel,0)+1#get(key,default)当key不存在时候默认值是default
sortedClassCount = sorted(classCount.items(), key=op.itemgetter(1), reverse=True)
# [('B', 2), ('A', 1)]
return sortedClassCount[0][0]#返回与其最近的k个邻居中,出现最多的次数
if __name__ == "__main__":
dataSet,labels=creatDataSet()
res=knnClassify([0,0],dataSet,labels,3)
print(res)

参考:
<<机器学习实战>>-Peter Harrington
<<算法图解>>-Aditya Bhargava

