插值查找
插值查找算法
算法思想
-
假如有一本英文的字典,你现在要查找apple这个单词,你肯定不会一页页去翻,也不会从中间去翻,你肯定会去前边翻,因为你知道字典是有序的,从A-Z,已知A在前面,所以你一定会去前面翻
-
同样的,对于一个值均匀增长的一个数组来说,已知一个值的大小,我们就可以按照值的分布规律来猜测它的下标
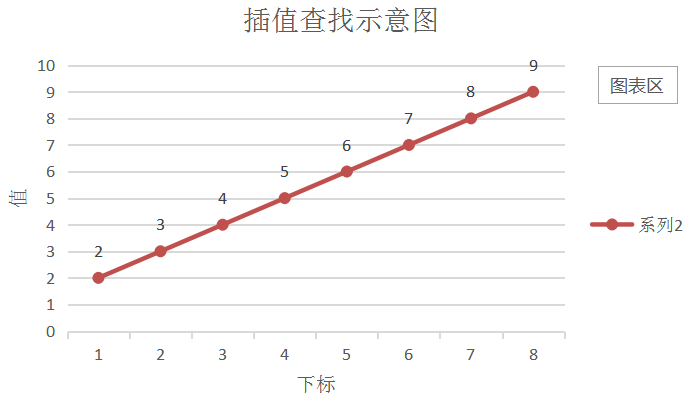
- 假设值随下标增加如上图所示,现在已知值求下标,那么通过函数公式可知道y-a[low] =(a[high]-a[low])/(high-low)(x-low),那么代入要查找的值key,就可以求出大概的下标index = low + (high - low)(key - a[low])/ (a[high] - a[low])
代码实现
package search;
public class InterpolationSearch {
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] a= {1,2,3,4,5,6,7,8,9};
int index=interpolationSearch(a, 6);
System.out.println(index);
}
public static int interpolationSearch(int[] a,int key)
{
int low=0;
int high=a.length-1;
int index;
while(a[low]!=a[high]&&key<=a[high]&&key>=a[low])//判断条件
{
index=low + (high - low)*(key - a[low])/(a[high] - a[low]);
if(a[index]==key)
{
return index;
}
else if(a[index]<key)
{
high=index-1;
}
else
{
low=index+1;
}
}
if(key==a[low])//针对重复元素
{
return low;
}
else
{
return -1;
}
}
}
注意
-
要保证这两个条件,不可以用while(low<=high),否则可能在查找不存在的值的时候陷入死循环
1.a[low]!=a[high] ( 插值公式里分母是a[high] - a[low],不能等于0)
2.a[low]<=key<=a[high] -
要考虑到都是重复元素的极端情况例如都是2,a=
特性
- 插值查找的时间复杂度是(logNlogN)
- 插值查找适合于元素有序且均匀分布的情况

