量子密钥分发的纠错算法Cascade
Cascade纠错算法是一种典型的随机校错算法。在量子密钥分发(QKD)里常用。在每一轮的传输结束,筛选(或对基)之后,Alice和Bob各有一组保密的密钥数组。由于系统的不完美,这两组密钥不一定相同。这时候就需要一种算法既能尽可能少的暴露隐私,又可以纠正误码比特。Cascade算法就是其中一种。它以很大的概率保证纠错后的两组密钥相同,但是并不保证100%相同,实际上Cascade只在误码率在1%左右时才能比较好地保证纠错后两组密钥相同。因此在纠错之后还要进行错误校验确定一下纠错后的密钥是不是真的相同。此算法流程如下:
- 确定纠错轮数N。
- 执行第一轮纠错。Alice将自己的密钥${ \left\{ k_{A,1}, k_{A,2},\cdots k_{A,m} \right\} }$随机分组,并将自己的分组方案发送给Bob。Bob收到之后把自己的密钥${ \left\{ k_{B,1}, k_{B,2},\cdots k_{B,m} \right\} }$按照A的方式也分组。然后逐组比对Alice和Bob的奇偶校验码,如果校验码不相同则用二分法纠错。保存此次的分组方案。
- 执行后续的第i轮纠错。Alice和Bob也像第一轮一样随机的给自己的密钥分组。然后逐组比对校验码。设现在纠错的是第j组。如果Alice和Bob的校验码不一样则进行二分法纠错,并记录此次错误比特${ k_{B,x} }$。从之前保存的分组方案中找到所有包含比特${ k_{B,x} }$的组,记为集合M。
- 从集合M中选择一个长度最小的组,可以断定该组必有误码。对该组用二分法纠错,并记录错误比特${ k_{ B,x^{'} } }$。再从此前保存的分组方案中找出所有包含比特${ k_{ B,x^{'} } }$的组,记为集合Q。
- 令${ M=\left( M \cup Q \right)-\left( M \cap Q \right) }$。即M等于M和Q的异或集。
- 如果M为空则结束这一个组的纠错过程,换下一组纠错,直到这一轮的所有组全都纠错完毕。同样地也要记录本次的分组方案。否则回到第3.1步。
- 达到设定轮数N流程结束。
上述的二分法纠错就是使用二分法对比奇偶校验码,直到最后组的区间长度为1的时候就可以确定这个比特是不是错误比特。比如,假设某一区间${ \left[ a,b \right) }$有错误比特,那么Alice和Bob要二分该区间,对比前半区间${ \left[ a,\frac{a+b}{2} \right) }$的校验码。如果校验码不相同说明错误比特在区间${ \left[ a,\frac{a+b}{2} \right) }$内,如果相同则说明错误比特在区间${ \left[ \frac{a+b}{2},b \right) }$内。在确定错误比特所在子区间之后,再次二分该子区间重复上述步骤直到找到错误比特的位置。区间${ \left[ a,b \right) }$的奇偶校验码计算方法是:${ e = \left( \sum_{i=a}^{b-1} k_{i} \right) \text{ mod } 2 }$。这个算法中还有如下几个方面要注意:
- 第3步对第j组进行纠错时,反复从M中选一个组纠错会导致第j组本身的奇偶校验码变化。比如:如果比特${ k_{ B,x^{'} } }$和比特${ k_{B,x} }$一样都属于第j组,那就意味着第j组就经过了两次纠错,此时它的奇偶校验码就回到未纠错时候的错误状态。所以在M为空结束时还要再次确认第j组的校验码是否变成了和Alice的一样,如果不相同还需要再次对第j组纠错直到它和Alice的校验码相同。算法要确保任何一个组在纠错之后它的校验码都和Alice中的一样。
- 第3步和3.1步从保存的分组方案中提取集合M和集合Q。要注意这里的提取范围时第1轮到第i-1轮,加上第i轮的第1组到第j-1组的所有历史分组。对集合M的迭代纠错可能会影响到第j组之前所有组的奇偶性。
- 第3步中要考虑组的区间重复的问题。主要原因是组是随机分割的,所以可能随机出相同的组。当前处理的第j组的区间可能已保存的记录中也有。
一般地,建议分组时尽可能在概率上让一个组里只有一个误码比特,并且随着循环的进行分组的区间长度逐渐增加。下面是我根据理论流程写的算法实现代码供参考:https://gitee.com/mengxiangdu/QtCascade.git。下面是这个程序的产生随机密钥时和纠错之后的截图:
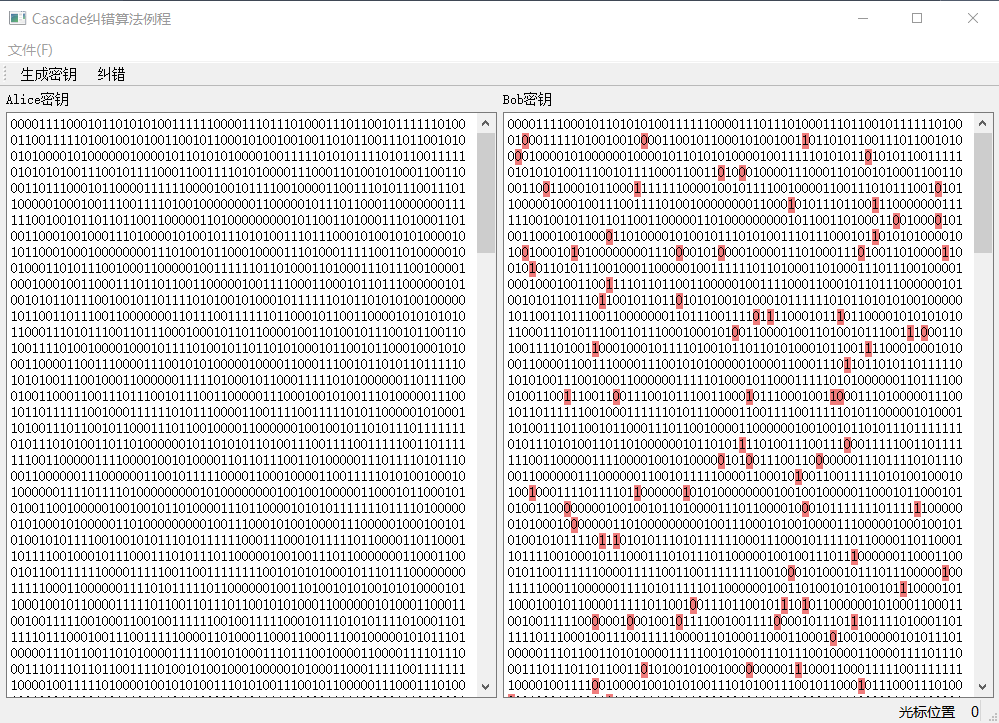
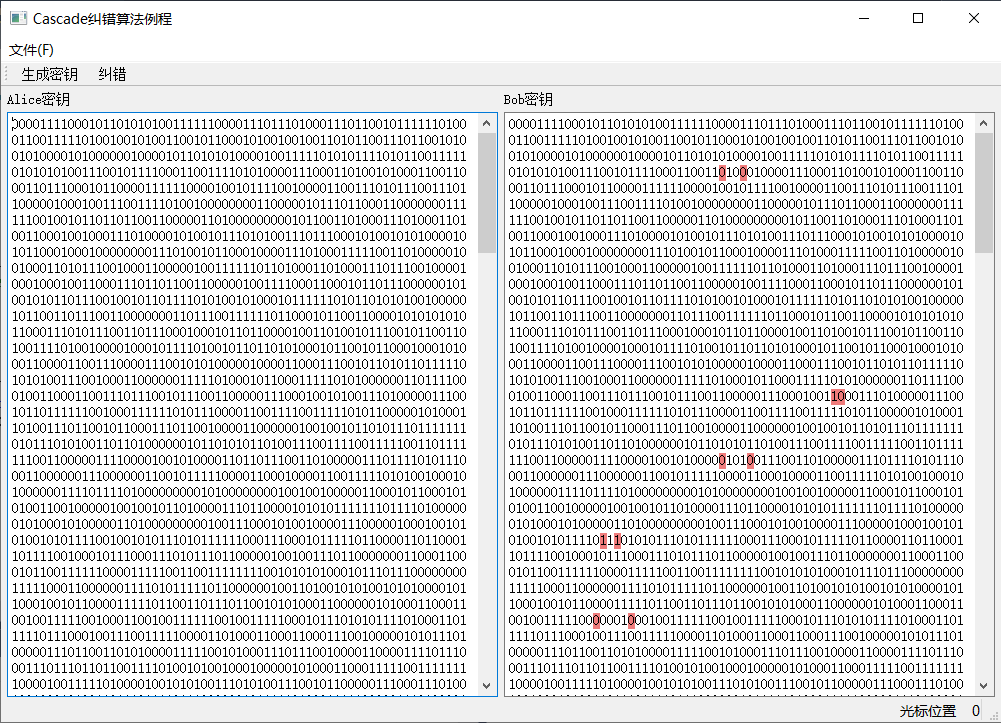
本文摘自论文《量子密钥分配中后处理技术及诱骗态技术研究》、《量子密钥分配后处理概述》和《Secret-Key Reconciliation by Public Discussion》。


