Jensen不等式

对于凸函数${ f \left( x \right) }$。不同书里的凸函数定义可能不一样，这里的凸函数指的是函数曲线向下凹陷的函数，有些书里叫它下凸函数。即函数的一阶导数单调递增，二阶导数大于等于0且不全为0。设${ \alpha \in \left[ 0,1 \right] }$则有：

$${ \alpha f\left( x \right) + \left( 1-\alpha \right) f\left( y \right) \geqslant f\left( \alpha x + \left( 1-\alpha \right)y \right) }$$

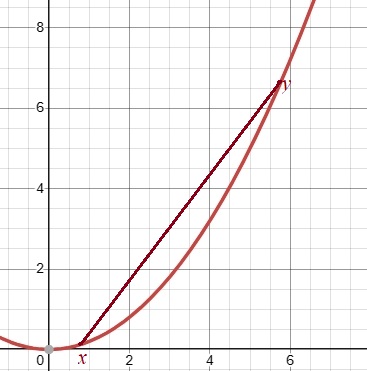
Jensen不等式则扩展了上式，将其推广到任意多个变量x, y。即对于凸函数${ f \left( x \right) }$，设有N个常数${ \alpha_{i} \geqslant 0 }$且${ \sum_{i=1}^{N}\alpha_{i}=1 }$，则有如下结论：

$${ \sum_{i=1}^{N}\alpha_{i}f\left( x_{i} \right) \geqslant f\left( \sum_{i=1}^{N}\alpha_{i}x_{i} \right) }$$

Jensen不等式可以用数学归纳法证明。证明过程如下：

在N=1时不等式显然成立。

在N=2时由凸函数定义可知不等式也成立。

我们假设N=n时不等式成立，那么只需要证明N=n+1时不等式也成立即可。

$${ \begin{align*} \sum_{i=1}^{n+1}\alpha_{i}f\left( x_{i} \right) &= \alpha_{n+1}f\left( x_{n+1} \right)+\sum_{i=1}^{n}\alpha_{i}f\left( x_{i} \right) \\ &= \alpha_{n+1}f\left( x_{n+1} \right)+\left( 1-\alpha_{n+1} \right)\sum_{i=1}^{n}\frac{\alpha_{i}}{1-\alpha_{n+1}}f\left( x_{i} \right) \\ &\geqslant \alpha_{n+1}f\left( x_{n+1} \right)+\left( 1-\alpha_{n+1} \right)f\left( \sum_{i=1}^{n}\frac{\alpha_{i}}{1-\alpha_{n+1}}x_{i} \right) \\ &\geqslant f\left( \alpha_{n+1}x_{n+1} + \left( 1-\alpha_{n+1} \right)\sum_{i=1}^{n}\frac{\alpha_{i}}{1-\alpha_{n+1}}x_{i} \right) \\  &=f\left( \alpha_{n+1}x_{n+1} + \sum_{i=1}^{n}\alpha_{i}x_{i} \right) \\ &=f\left( \sum_{i=1}^{n+1}\alpha_{i}x_{i} \right) \end{align*} }$$

所以，N=n+1时不等式也成立。