匹配位姿拟合求精方法
在机器视觉中,有多种方法可用于灰度匹配或轮廓匹配等的亚像素求精。本文方法来源是论文《基于几何特征的快速模板匹配算法》。一般匹配算法有3个以上的自由度。本文以3个自由度为例。在粗匹配流程中一般是逐像素和以${ \Delta\theta }$为步长遍历取得最优的像素级位姿${ \left( x_{0},y_{0},\theta_{0} \right) }$。位姿即平移和旋转量。然后用某种方法求精,本文介绍如下两种方法。
一、根据位姿相似度直接拟合
该方法适用于各种不同的匹配算法。但是精确度稍低。它以像素级姿态附近3×3×3个位姿和对应的相似度值使用最小二乘法拟合多项式函数得到稍微精确的结果。我们可以设定拟合函数为:
$${ \begin{equation} z=ax^{2}+by^{2}+c\theta^{2}+dxy+ex\theta+fy\theta+gx+hy+i\theta+j \end{equation} }$$
这里不缀述怎么拟合这个函数了,可参见文章《9点拟合梯度边缘亚像素方法 - 兜尼完 - 博客园 (cnblogs.com)》。相似地也可以通过平移${ \left( x_{0},y_{0},\theta_{0} \right) }$坐标至原点并且把${ \Delta\theta }$视为1简化运算。最终可得公式:
$${ \begin{pmatrix} a \\ b \\ c \\ d \\ e \\ f \\ g \\ h \\ i \\ j \end{pmatrix} = \mathbf{K_{10 \times 27}} \begin{pmatrix} z\left(-1,-1,-1 \right) \\ z\left(-1,-1,0 \right) \\ z\left(-1,-1,1 \right) \\ z\left(-1,0,-1 \right) \\ z\left(-1,0,0 \right) \\ z\left(-1,0,1 \right) \\ z\left(-1,1,-1 \right) \\ z\left(-1,1,0 \right) \\ z\left(-1,1,1 \right) \\ \vdots \\ z\left(1,1,1 \right) \end{pmatrix} }$$
其中常量矩阵${ \mathbf{K_{10 \times 27}} }$可通过以下代码得到。需要OpenCV库,结果保存在coe.txt中。
int main() { float data[27][10]; for (int i = -1; i <= 1; i++) /* x */ { for (int j = -1; j <= 1; j++) /* y */ { for (int k = -1; k <= 1; k++) /* theta */ { int row = (i + 1) * 9 + (j + 1) * 3 + k + 1; data[row][0] = i * i; data[row][1] = j * j; data[row][2] = k * k; data[row][3] = i * j; data[row][4] = i * k; data[row][5] = j * k; data[row][6] = i; data[row][7] = j; data[row][8] = k; data[row][9] = 1; } } } Mat x(27, 10, CV_32FC1, data); Mat z = (x.t() * x).inv() * x.t(); std::ofstream fs("D:/coe.txt"); for (int i = 0; i < z.rows; i++) { for (int j = 0; j < z.cols; j++) { fs << (j ? " " : "\n"); fs << z.at<float>(i, j); } } return 0; }
接下来就是计算亚像素量。对(1)式求偏导数并令其为0可得方程组:
$${ \left\{\begin{matrix} \frac{\partial z}{\partial x} =2ax+dy+e\theta+g=0 \\ \frac{\partial z}{\partial y} =2by+dx+f\theta+h=0 \\ \frac{\partial z}{\partial \theta} =2c\theta+ex+fy+i=0 \end{matrix}\right. }$$
解之得亚像素量,为了区分这里用${ x^{'},y^{'},\theta^{'} }$表示:
$${ \begin{pmatrix} x^{'} \\ y^{'} \\ \theta^{'}\end{pmatrix}=\begin{pmatrix} 2a & d & e \\ d & 2b & f \\ e & f & 2c \\ \end{pmatrix}^{-1}\begin{pmatrix} -g \\ -h \\ -i \end{pmatrix} }$$
那么高精度位姿为:
$${ \left\{\begin{matrix} x_{sub}=x_{0}+x^{'} \\ y_{sub}=y_{0}+y^{'} \\ \theta_{sub}=\theta_{0}+\theta^{'}\cdot \Delta\theta \end{matrix}\right. }$$
另外插一嘴,对(1)式的拟合除了上述的直接应用最小二乘法之外还有其他方法。可参考论文《2304.00517.pdf (arxiv.org)》。这篇论文虽然标题是关于椭球面的拟合,但实际内容却是拟合一个普通的二次曲面,因为它没有对待求函数施加任何条件限制。其方法是对二次型求最小值,也是线性代数相关的知识。
二、根据边缘点信息拟合
该方法适用于基于轮廓的匹配算法。它通过最小化模板中的边缘点和模板在像素级位姿${ \left( x_{0},y_{0},\theta_{0} \right) }$时对应的运行图像的边缘点切线的距离来确定高精度位姿。如下图所示,绿色是模板图像,包含边缘点P1,P2…(已知的);红色是运行图像,包含边缘点Q1,Q2…。经过粗匹配模板和运行图像中的边缘基本对齐但略有偏差,如P1对应Q1,P2对应Q2…。Q1,Q2…是根据P1,P2…的位置在它们附近找到的近似的对应点。要获取更精确的模板位姿只需最小化Pn到Qn的切线ln的距离即可。
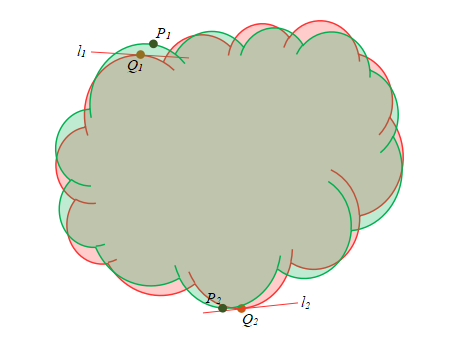
从以上叙述中可知我们需要计算运行图像的边缘点Qn的切线。可以通过Sobel算子得到Qn的梯度,单位化后记为${ \left( G_{x,n},G_{y,n} \right) }$,然后可得到切线ln方程如下:
$${ a_{n}x+b_{n}y-c_{n}=0,其中a_{n}=G_{x,n},b_{n}=G_{y,n},c_{n}=G_{x,n}Q_{x,n}+G_{y,n}Q_{y,n} }$$
从而待优化的目标函数是:
$${ e=\sum_{n=1}^{N} \left[ a_{n} \left(P_{x,n}cos d_{\theta}-P_{y,n}sin d_{\theta}+d_{x} \right)+b_{n} \left(P_{x,n}sin d_{\theta}+P_{y,n}cos d_{\theta}+d_{y} \right) -c_{n} \right]^{2} }$$
上式中${ d_{x},d_{y},d_{\theta} }$是模板旋转平移微调量。由于亚像素优化的量很小,因此有${ cos d_{\theta} \approx 1,sin d_{\theta} \approx d_{\theta} }$,从而化简上式:
$${ \begin{align*} e&=\sum_{n=1}^{N} \left[ a_{n} \left(P_{x,n}-P_{y,n} d_{\theta}+d_{x} \right)+b_{n} \left(P_{x,n} d_{\theta}+P_{y,n}+d_{y} \right) -c_{n} \right]^{2} \\ &=\sum_{n=1}^{N} \left[ a_{n}d_{x}+b_{n}d_{y} + \left(b_{n}P_{x,n}-a_{n}P_{y,n} \right) d_{\theta} + a_{n}P_{x,n}+b_{n}P_{y,n}-c_{n} \right]^{2} \\ &=\sum_{n=1}^{N} \left( a_{n}d_{x}+b_{n}d_{y} + S_{n} d_{\theta} + T_{n} \right)^{2},其中S_{n}=b_{n}P_{x,n}-a_{n}P_{y,n},T_{n}=a_{n}P_{x,n}+b_{n}P_{y,n}-c_{n} \end{align*} }$$
接下来都是老生常谈的内容,求偏导数使其为0得到方程组:
$${ \left\{ \begin{matrix} \frac{\partial e}{\partial d_{x}}=2\sum_{n=1}^{N}a_{n} \left( a_{n}d_{x}+b_{n}d_{y} + S_{n} d_{\theta} + T_{n} \right)=0 \\ \frac{\partial e}{\partial d_{y}}=2\sum_{n=1}^{N}b_{n} \left( a_{n}d_{x}+b_{n}d_{y} + S_{n} d_{\theta} + T_{n} \right)=0 \\ \frac{\partial e}{\partial d_{\theta} }=2\sum_{n=1}^{N} S_{n} \left( a_{n}d_{x}+b_{n}d_{y} + S_{n} d_{\theta} + T_{n} \right)=0 \end{matrix} \right. }$$
最终得到模板微调量的解为:
$${ \begin{pmatrix} d_{x} \\ d_{y} \\ d_{\theta} \end{pmatrix}=\begin{pmatrix} \sum_{n=1}^{N}a_{n}^{2} & \sum_{n=1}^{N}a_{n}b_{n} & \sum_{n=1}^{N}a_{n}S_{n} \\ \sum_{n=1}^{N}a_{n}b_{n} & \sum_{n=1}^{N}b_{n}^{2} & \sum_{n=1}^{N}b_{n}S_{n} \\ \sum_{n=1}^{N}a_{n}S_{n} & \sum_{n=1}^{N}b_{n}S_{n} & \sum_{n=1}^{N}S_{n}^{2} \end{pmatrix}^{-1}\begin{pmatrix} -\sum_{n=1}^{N}a_{n}T_{n} \\ -\sum_{n=1}^{N}b_{n}T_{n} \\ -\sum_{n=1}^{N}S_{n}T_{n} \end{pmatrix} }$$
将求得的微调量叠加到原始的位姿上就可以了。注意不是简单的数值相加,而是位姿对应的刚性变换矩阵的相乘。另外需要知道有些应用在优化时会反过来优化模板中的边缘点的切线和模板在位姿${ \left( x_{0},y_{0},\theta_{0} \right) }$时对应的运行图像的边缘点的距离。即模板不变,微调运行图像的位姿来达到目的。理由是模板中的边缘点及其梯度是已知的,可以节省求切线的时间,并且通常模板中的边缘质量较好而运行图像中的边缘则无法控制可能受噪声影响。甚至更进一步可以在创建模板的时候扩展边缘,直接把边缘点附近的点到它们最近的边缘点的距离方向等数据保存起来以节省查找模板和运行图像对应边缘点的时间。


