量子密钥分发的误码估计方法

量子密钥分发主要包括量子信号传输阶段和后处理阶段。量子信号传输阶段主要完成的是在Alice和Bob之间进行的量子态的发送、传输和测量过程。后处理阶段主要包括对基、误码估计、密钥协商、错误校验和保密放大过程（需要注意后处理阶段是在可信认证的经典信道中进行的，即窃听者可以窃听但是不能篡改其中的内容）。流程如下图所示：

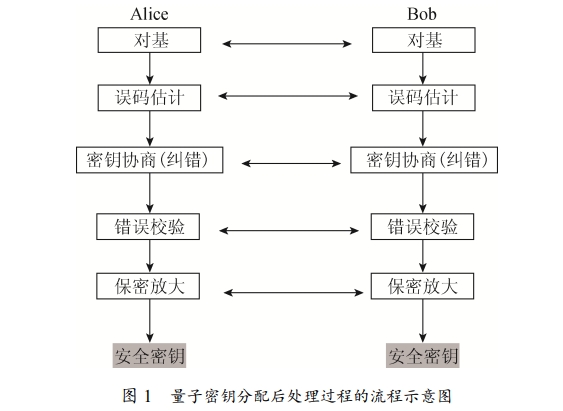
本文叙述的是上图“误码估计”的过程。一般有三种方法，分别是：

1. 随机抽样法
2. 分组奇偶校验法
3. 最大似然估计法

一、随机抽样法

该方法简单易行，是将${ \left( k_{1},k_{2},\cdots k_{l} \right)_{Alice} }$和${ \left( k_{1},k_{2},\cdots k_{l} \right)_{Bob} }$中随机抽取一定量的密钥进行比对，将抽取的样本的不一致率认为就是Alice和Bob筛后密钥的误码率，本质上是一种以部分代替全部的方法。

二、分组奇偶校验法

奇偶校验法是将Alice和Bob各自的密钥相应地分成许多小段（一般可以10个比特左右一组）继而将每段的奇偶校验和进行对比，根据校验和的错误率，最后通过数学的计算反推估计出一个筛后密钥的误码率。若分组大小为g，则Alice和Bob将其筛后密钥分组为：

$${ \left( k_{1},k_{2},\cdots k_{g} \right)_{Alice},\left( k_{g+1},k_{g+2},\cdots k_{2g} \right)_{Alice},\cdots \left( k_{l-g+1},k_{l-g+2},\cdots k_{l} \right)_{Alice} }$$

$${ \left( k_{1},k_{2},\cdots k_{g} \right)_{Bob},\left( k_{g+1},k_{g+2},\cdots k_{2g} \right)_{Bob},\cdots \left( k_{l-g+1},k_{l-g+2},\cdots k_{l} \right)_{Bob} }$$

记第i个分组为${ K_{i} \left( 1 \le i \le l/g \right) }$。而后双方对每个分组做校验求和，记${ K_{i} }$的校验和为

$${ G_{i}=\left( \sum_{k_{j} \in K_{i} } k_{j} \right) \text{ mod } 2 }$$

下一步对比Alice和Bob的${ G_{i} }$值。若Alice和Bob的${ G_{i} }$不相等, 则可知在${ K_{i} }$中有奇数个错误。进而求出这些奇偶校验和的错误率${ e_{ check } }$。它和筛后密钥的误码率e有如下关系：

$${ e_{check}=0.5+0.5 \cdot (1-2e)^{g} }$$

移项后可得我们估计的筛后密钥误码率为：

$${ e=0.5+0.5 \cdot (1-2e_{check})^{\frac{1}{g} } }$$

经过验证，该方法适用于误码率较低的情况。因上式要求${ 1-2e_{check} \ge 0 }$。在实际测试中误码率大于15%之后基本就无法求出e的值了。下面是测试用的代码。代码中TOTAL_SUM是总的密钥数量，GROUP_SIZE是分组大小，Point2i是OpenCV中表示平面坐标的结构体，可以认为pairs[i].x是Alice的密钥，pairs[i].y是Bob的密钥：

#define TOTAL_SUM 50000
#define GROUP_COUNT 5000
#define GROUP_SIZE 10

int main()
{
    srand((int)time(0));

    std::vector<Point2i> pairs;
    /* 这里随机产生密钥 */
    for (int i = 0; i < TOTAL_SUM; i++)
    {
        int value = rand() % 2;
        int equal = ((rand() % 100) >= 12);
        pairs.push_back(Point2i(value, equal ? value : (1 - value)));
    }

    int rcount = 0;
    for (int i = 0; i < TOTAL_SUM; i++)
    {
        rcount += (pairs[i].x != pairs[i].y);
    }
    /* 遍历计算真实误码率 */
    float realQber = float(rcount) / TOTAL_SUM;

    vector<int> Ga, Gb;
    for (int i = 0; i < GROUP_COUNT; i++)
    {
        int gga = 0;
        int ggb = 0;
        for (int j = 0; j < GROUP_SIZE; j++)
        {
            gga += pairs[GROUP_SIZE * i + j].x;
            ggb += pairs[GROUP_SIZE * i + j].y;
        }
        gga &= 1;
        ggb &= 1;
        Ga.push_back(gga);
        Gb.push_back(ggb);
    }
    int error = 0;
    for (int i = 0; i < GROUP_COUNT; i++)
    {
        error += (Ga[i] != Gb[i]);
    }
    float ratio = float(error) / GROUP_COUNT;
    /* 用奇偶校验法得到的误码率 */
    float estimateQber = 0.5f - 0.5f * powf(1 - 2 * ratio, 1.0f / GROUP_SIZE);

    return 0;
}

第三种方法由于没找到相关文献，这里不再叙述。本文内容摘自《量子密钥分配后处理概述》和《量子密钥分配中后处理技术及诱骗态技术研究》这两篇论文，有改动。