神经网络学习之----受限玻尔兹曼机RBM
转载:https://www.cnblogs.com/jiangxinyang/p/9307573.html
受限玻尔兹曼机(RBM)是一个随机神经网络(即当网络的神经元节点被激活时会有随机行为,随机取值)。它包含一层可视层和一层隐藏层。在同一层的神经元之间是相互独立的,而在不同的网络层之间的神经元是相互连接的(双向连接)。在网络进行训练以及使用时信息会在两个方向上流动,而且两个方向上的权值是相同的。但是偏置值是不同的(偏置值的个数是和神经元的个数相同的),受限玻尔兹曼机的结构如下

上面一层神经元组成隐藏层(hidden layer), 用h向量隐藏层神经元的值。下面一层的神经元组成可见层(visible layer),用v向量表示可见层神经元的值。连接权重可以用矩阵W表示。和DNN的区别是,RBM不区分前向和反向,可见层的状态可以作用于隐藏层,而隐藏层的状态也可以作用于可见层。隐藏层的偏倚系数是向量b,而可见层的偏倚系数是向量a。
常用的RBM一般是二值的,即不管是隐藏层还是可见层,它们的神经元的取值只为0或者1。
RBM模型结构的结构:主要是权重矩阵W, 偏倚系数向量a和b,隐藏层神经元状态向量h和可见层神经元状态向量v。
能量函数和概率分布
RBM是基于基于能量的概率分布模型。分为两个部分:第一部分是能量函数,第二部分是基于能量函数的概率分布函数。对于给定的状态向量h和v,则RBM当前的能量函数可以表示为:
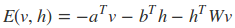
其中a,b是偏倚系数,而W是权重矩阵。有了能量函数,v,h的联合概率分布为:
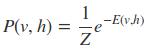
其中Z是被称为配分函数的归一化常数(对于概率输出一般都要做归一化):
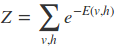
由于配分函数Z的难以处理,所以必须使用最大似然梯度来近似。首先从联合分布中导出条件分布:
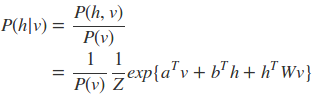
为了推导方便将无关值归于Z’中:
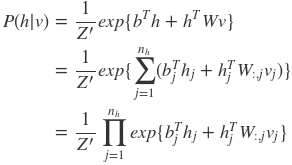
可以容易的得到在给定可视层v的基础上,隐层第j个节点为1或者为0的概率为:
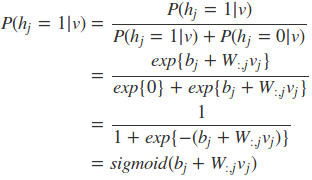
可以看到就是相当于使用了sigmoid激活函数,现在可以写出关于隐藏层的完全条件分布:
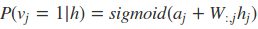
有了激活函数,我们就可以从可见层和参数推导出隐藏层的神经元的取值概率了。对于0,1取值的情况,则大于0.5即取值为1。从隐藏层和参数推导出可见的神经元的取值方法也是一样的。
RBM损失函数
RBM模型的关键就是求出我们模型中的参数W,a,b。首先我们得写出损失函数,RBM一般采用对数损失函数,即期望最小化下式:

然后求偏导可得:
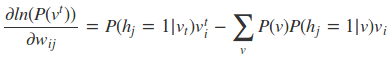
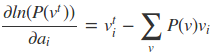
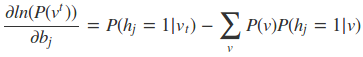
虽然说梯度下降从理论上可以用来优化RBM模型,但实际中是很难求得P(v)的概率分布的(P(v)表示可见层节点的联合概率)。计算复杂度非常大,因此采用一些随机采样的方法来得到近似的解。看这三个梯度的第二项实际上都是求期望,而我们知道,样本的均值是随机变量期望的无偏估计。因此一般都是基于对比散度方法来求解。
对比散度算法(CD)
CD算法大概思路是这样的,从样本集任意一个样本v0开始,经过k次Gibbs采样(实际中k=1往往就足够了),即每一步是:

得到样本vk,然后对应于上一篇三个单样本的梯度,用vk去近似:
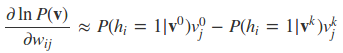
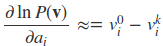

上述近似的含义是说,用一个采样出来的样本来近似期望的计算。下面给出CD-k的算法执行流程。

具体RBM算法的流程:

深度玻尔兹曼机(DBM)
加深RBM的层数后,就变成了DBM,结构图如下:
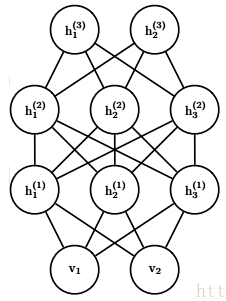
此时的能量函数变为:

联合概率变成:
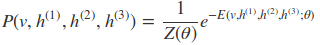
其实DBM也可以看做是一个RBM,比如对上图稍微加以变换就可以看做是一个RBM。

将可见层和偶数隐藏层放在一边,将奇数隐藏层放在另一边,我们就得到了RBM,和RBM的细微区别只是现在的RBM并不是全连接的,其实也可以看做部分权重为0的全连接RBM。RBM的算法思想可以在DBM上使用。只是此时我们的模型参数更加的多,而且迭代求解参数也更加复杂了。



