seq2seq和Transformer
简单而言,seq2seq由两个RNN组成,一个是编码器(encoder),一个是解码器(decoder).以MT为例,将源语言“我爱中国”译为“I love China”,则定义序列:
另外目标序列:
通过编码器将\(X=(x_0,x_1,x_2,x_3)\)映射为隐层状态\(h\),再经由解码器将\(h\)映射为\(Y=(y_0,y_1,y_2)\)
通常使用\(h\)表示编码器的隐状态;用\(s\)表示解码器的隐状态
注意:编码器输入和解码器输出向量的维度可以不同,最后将预测T和真实目标序列T‘做loss(通常是交叉熵)训练网络。
注意力机制
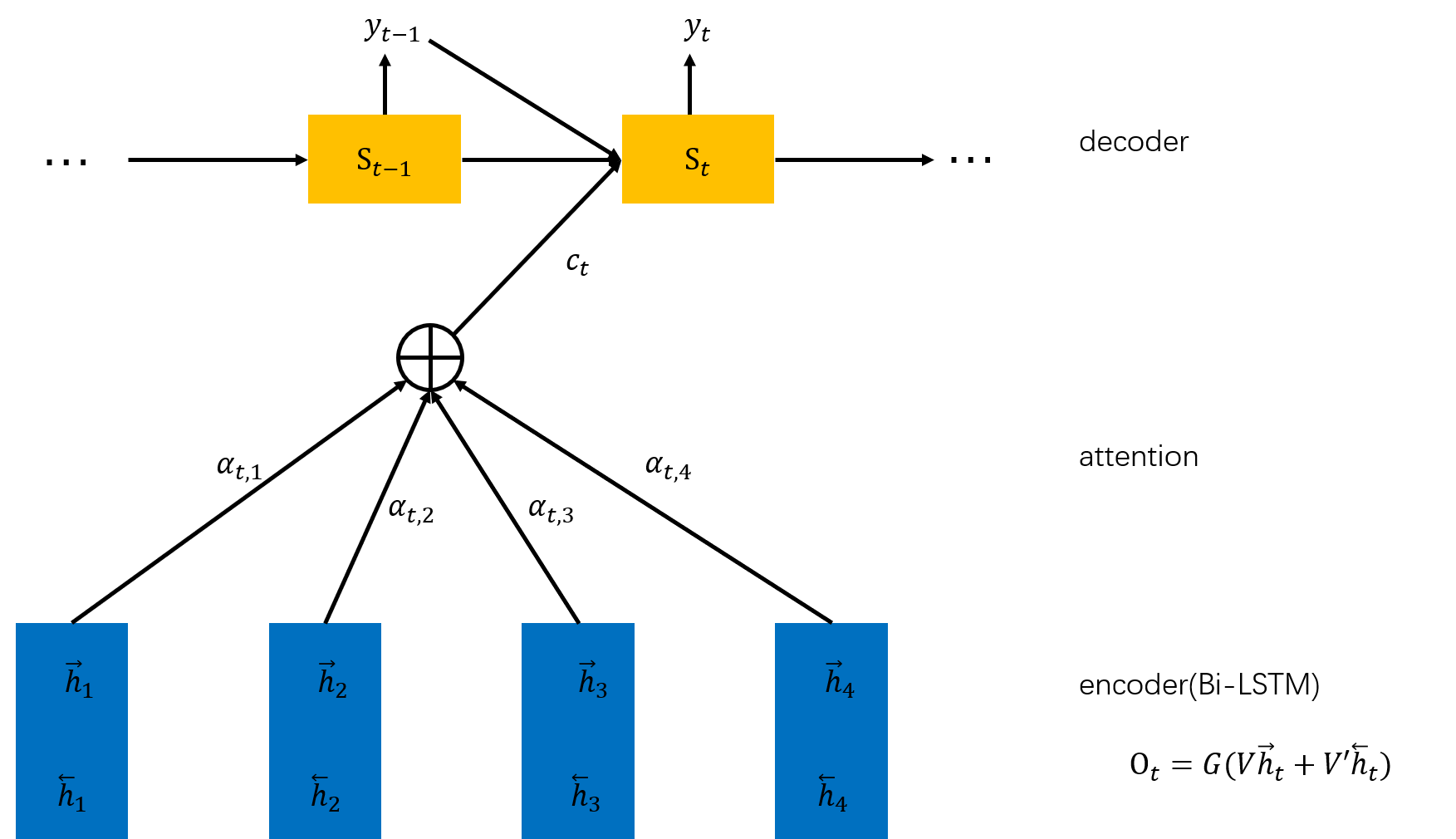
通过编码器,把\(X=(x_1,x_2,x_3,x_4)\)映射为一个隐层状态\(H=(h_0,h_1,h_2,h_3)\),解码器将\(H=(h_0,h_1,h_2,h_3)\)映射为\(Y=(y_0,y_1,y_2)\)。在带注意力机制的编解码器中,\(Y\)中的每一个元素都与\(H\)中的所有元素相连,而解码器的每个元素通过不同的权值给予编码器输出\(Y\)不同的贡献。
解码器输出有3个:
-
上一解码步的隐状态(\(s_{t-1}\))
-
上一解码步的输出(\(y_{t-1}\))
-
注意力输出(编码器输出的加权和,context,是编码器端发给解码器信息的地方,由所有的编码器输出得到一个定长的向量,代表输入序列的全局信息,作为当前解码步的上下文),计算方法为:
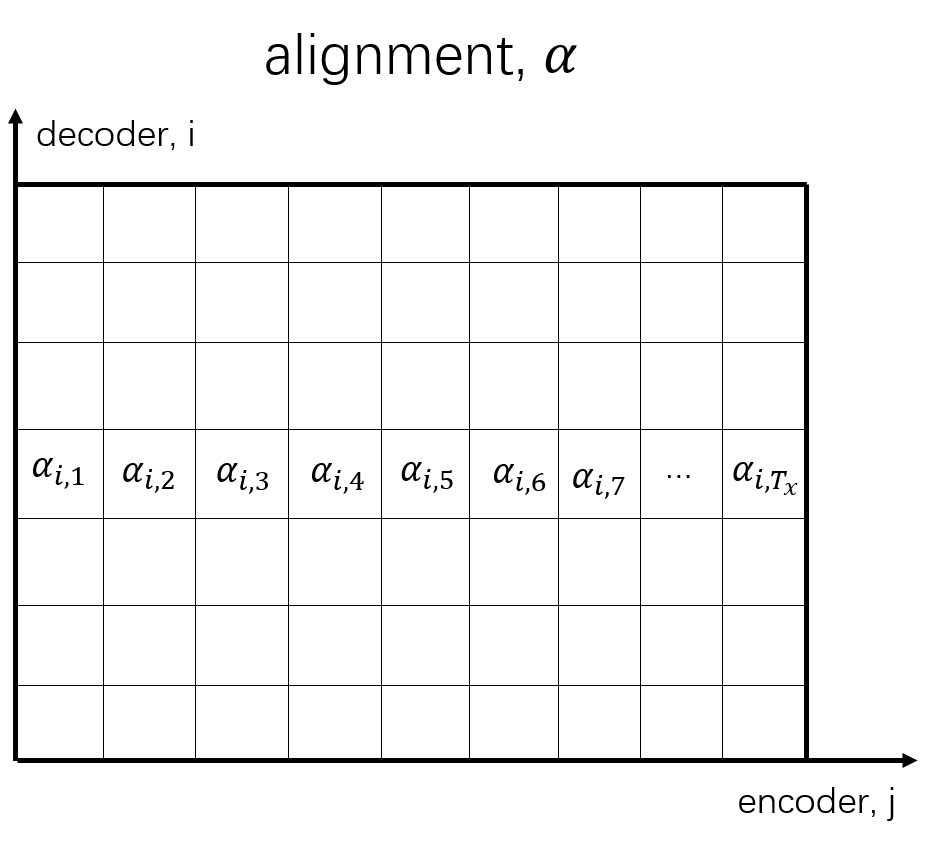
\[c_i=\sum_{j=1}^{T_x}\alpha_{ij}h_j \]其中,\(\alpha_{ij}\)是权重(\(\alpha_{ij}\)是标量,\(\alpha\)是二阶张量),又称作alignment;\(h\)是编码器所有时间步上的隐状态,又称作value或memory;\(i\)表示解码步,\(j\)表示编码步,输出\(c_i\)是和\(h_j\)同样大小的向量。
![]()
在时间\(i\)上,
\[c_i=\sum_{j=1}^{T_x}\alpha_{ij}h_j=\alpha_{i,1}h_1+\alpha_{i,2}h_2+...+\alpha_{i,T_x}h_{T_x} \]其中,\(c_i\)是与编码器输出\(h_j\)等大的向量;\(j\)为编码步;\(i\)为解码步;\(\alpha_{ij}\)为标量,计算方式:
\[\alpha_{ij}=\frac{exp(e_{ij})}{\sum_{k=1}^{T_x}exp(e_{ik})} \]其中,\(e_{ij}=a(s_{i-1,j},h_j)\),表征\(s_{i-1}\)和\(h_j\)的相关程度,即对于某个给定的解码步,计算上一解码步的隐状态和所有编码步输出的相关程度,并且用softmax做归一化。这样,与上一解码步状态相关度大的编码器输出\(h\)的权重就大,在本解码步的整个上下文里面所占的比重就多,解码器在本时间步上解码时就越依赖这个编码器的输出\(h\).
\(e_{ij}\)又被称作能量函数,\(a(·)\)的计算方法:
- 对\(s_{i-1}\)做线性映射,得到向量作为query(解码器上一时间步隐状态作为“查询”),记作\(q_i\)
- 对\(h_j\)做线性映射,得到向量作为key(编码器每一个时间步上的结果作为key待查),记作\(k_j\)
- \(e_{ij}=v^T(q_i+k_j)\),\(q_i\)和\(k_j\)的维度必须相同,同为d维;\(v\)是一个d×1的向量,从而得到的\(e_{ij}\)是一个标量
1、2中的线性映射都是待训练的,3中的\(v\)也是待训练的。
对query和key求相关性从而获得权重(alignment),用该权重对value加权和从而得到上下文送入解码器。
小结
- 3中query和key做加法,之后通过一个权重变为标量。这被称作“加性注意力”,相应的,可以做元素乘,被称作“乘性注意力”
- location-sensitive,认为相邻\(\alpha_{ij}\)之间的关系会相对较大,为了捕获这种关系对alignment进行了卷积。
- query有多种,不仅仅有上一解码步的隐状态;也有当前解码步的隐状态;还有将上一解码步上的隐状态和上一解码步的输出拼接作为query。但在TTS中,将上一解码步的隐状态和输出拼接作为query并不好,原因可能是可能两者不在同一空间,因此要具体问题具体分析。
Transformer

-
左右分别是编码器和解码器
-
编码器和解码器的底部都是embedding,而embedding又分为两部分:
input embedding和positional embedding,其中input embedding就是NLP中常见的词嵌入。因为Transformer中只有attention,对于一对(query, key),无论这对query-key处在什么位置,其计算都是相同的。不像CNN或RNN有一个位置或时序的差异:CNN框住的是一块区域,随着卷积核的移动,卷积核边缘的点也随着有序变化;RNN则更为明显,不同时序的\(h_t\)和\(s_t\)不同,而且是随着输入顺序(正/倒序)而不同。因此Transformer为了体现出时序或者序列中的位置差异,要对input加入一定的位置信息,这即是position embedding。求位置id为pos的位置编码向量:
\[\left\{\begin{matrix} PE(pos,i)=sin(\frac{pos}{10000^{\frac{i}{d_{model}}}}),\ 若i为奇数 \\ PE(pos,i)=cos(\frac{pos}{10000^{\frac{i}{d_{model}}}})\ 若i为偶数 \end{matrix}\right. PE向量第i维的求解方法 \]编码器和解码器输入序列shape: \([T,d_{model}]\),即每个时刻的\(x_i\)都是\(d_{model}\)维的,因此\(pos\in [0,T]\),\(i\in[0,d_{model}]\)。即对于输入的\([T,d_{model}]\)的一个张量,其中的每一个标量都对应一个独特的编码结果,可以理解为给embedding一个低频信号,让其周期性波动,而且每个维度波动都不相同,以表征其id信息。
-
编码器和解码器的中部分别是两个块,分别输入一个序列,输出一个序列,这两个块重复N次。编码器的每个块里有两个子网,分别为Multi-Head Attention和Feed Forward Network(FFN);解码器的每个块里有三个子网,分别是2个Multi-Head Attention和一个FFN。这些子网之后都跟一个add & norm,就是像ResNet那样做一个残差,然后加一个layer normalization。
-
解码器最后还有个linear和softmax
FFN
FFN就是对一个输入序列\(X=(x_0,x_1,...,x_T)\),对每一个\(x_i\)都进行一次channel的重组:512 -> 2048 -> 512,可以理解为对每个\(x_i\)进行两次线性映射,也可以对整个序列进行1×1卷积。
Multi-Head Attention
原始的attention就是一个query(Q)和一组key(K)算相似度,然后对一组value(V)做加权和。假如每个Q和K都是512维的向量,就相当于在512维的空间里比较两个向量的相似度。而Multi-Head相当于加过于512维的空间人为拆分为多个子空间,如head number=8就是将高维空间拆分为8个子空间,相应地V也要分为8个head,然后在这8个子空间中分别计算Q和K的相似度,再组合V。这样能使attention从不同角度捕获序列关系。
-
编码器
\[sub\_layer\_output=LayerNorm(x+SubLayer(x))\\ head_i=Attention(QW_i^Q,KW_i^K,VW_i^K)\\ MultiHead(Q,K,V)=concat(head_1,head_2,...,head_h)W^O \]self-attention时,Q、K、V相同
-
解码器
-
输入:编码器的输出 & 对应i-1时刻的解码器输出(i-1步的hidden state和i-1步的输出)
注意:在解码器中间的attention不是self-attention,其K、V来自编码器,Q来自上一时刻的解码器输出
-
输出:i时刻的输出词的概率分布
-
解码:编码可以并行,一次性全部编码出来(在编码时,各个计算互不依赖)。但解码不是一次把所有序列解出来,而是如同RNN一样,一个一个解出来,因为要用到上一解码步的隐状态作为attention的query。解码器端最先的Multi-Head是Masked,这是因为训练时输入是ground truth,这样确保预测第i个位置时,遮蔽掉该位置及其之后的信息,不会接触未来的信息。
-
Transformer优缺点
-
优点
-
并行计算,这主要体现在编解码器都放弃了RNN,下一个时间步的计算不必等待之前的计算完全展开
-
直接的长距离依赖
原来的RNN中,第一帧要和第十帧发生关系,必须通过第二~九帧传递,进而产生两者的计算。而在这个过程中,第一帧的信息有可能已经产生了偏差,准确性和速度都难以保证。在Transformer中,由于self-attention的存在,任意两帧都有直接的交互,建立直接依赖。
-
-
缺点
仍然是自回归模型,任意一帧的输出都依赖于它之前的所有输出。比如输入
abc,本次的输出实际是bcd,每输入一个序列,其实序列的末端都只是前进了一帧,因此要生成abcdefg仍然要循环6次。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号