深度网络中的Tricks
- 数据增强(Data augmentation)
- 预处理(Pre-processing)
- 初始化(Initializations)
- 训练中的Tricks
- 激活函数(Activation functions)
- 正则化(Regularizations)
- 画图洞察数据
- 集成学习(Ensemble)
数据增强
深度学习需要大量的数据,当数据集不够大时,可以利用合理手段,基于已有数据,“创造”新的数据。本部分针对图像处理
对于图像而言,可以随机选择以下手段:
- 翻转
- 旋转
- 拉伸
- 裁剪
- 颜色抖动
- 光学畸变
能够采用这些手段的主要原因是,上述方法并不改变图像“语义”。



事实上,一些开源库如Keras已经集成了图像数据增强工具,如图片预处理-Keras,在图片生成器(ImageDataGenerator)中存在很多参数,用于控制数据增强。至于哪种手段有效,都试试就知道:)参见数据增强方法总结
自然语言处理领域,数据增强手段较为少见。
预处理
-
零中心化(zero-center),又称零均值化、中心化
\[x^*=x-\mu \]实质是一个平移过程,平移后所有数据的中心是\((0,0)\)
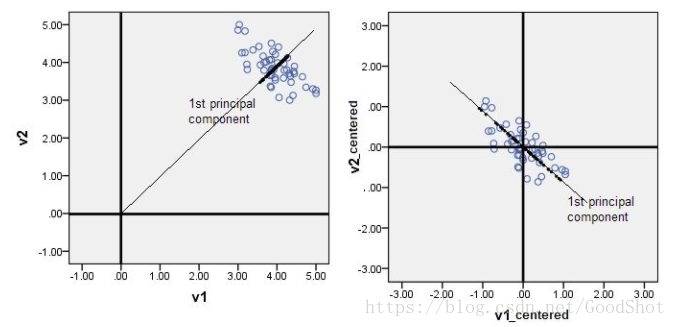
以主成分分析(PCA)为例,说明中心化的作用。
![]()
上图左侧数据未进行中心化,在主成分分析寻找数据点的特征向量时,会获得“错误”的主成分(黑线所示)。而右侧数据进行中心化之后,计算获得的主成分能够较好的“概括”原始数据。
-
标准化(normalization),又称归一化
通常有两种方式:
-
min-max标准化
又称离差标准化,对原始数据线性变换,映射到\([0,1]\)之间
\[x^*=\frac{x-min}{max-min} \] -
Z-score标准化
使用均值和标准差对原始数据做标准化,经处理的数据符合标准正态分布,\(x^*\sim N(0,1)\)
\[x^*=\frac{x-\mu}{\sigma} \]其中\(\mu\)为样本均值,\(\sigma\)为样本标准差
标准化主要是为了消除原始数据量纲不同对分析带来的影响,标准化后的数据在各个维度上”尺度“是一致的。以KMeans为例,使用欧式距离衡量两个样本点之间的距离时,假设样本部分特征的取值范围为\([-1000,1000]\),而部分特征的取值范围为\([-1,1]\),如果不进行标准化,这两类特征在计算距离时所占的”重要程度“就不一致,从而造成算法失效。
-
上图展示了零中心化和标准化的处理效果。参见数据预处理之中心化(零均值化)与标准化(归一化)
-
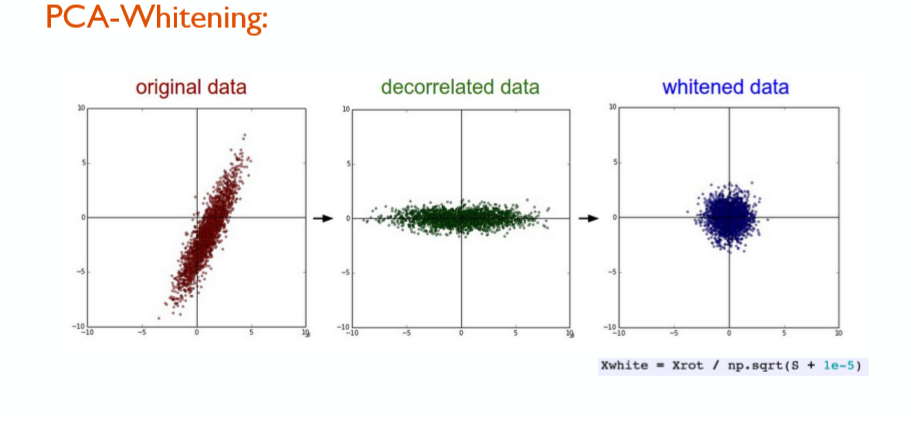
白化(whitening)
又称sphering,白化一般在去相关操作的基础之上,以PCA白化为例。PCA是一种数据降维算法,PCA降维主要就是将相关特征去除:
\[x_{rot}=U^Tx=\begin{bmatrix} u_1^Tx^1\\ u_2^Tx^2\\...\\u_n^Tx^n\end{bmatrix} \]其中,\(U\)为特征矩阵。参见主成分分析-UFLDL
白化的主要目的是降低输入的冗余性,即希望处理后的数据:1)特征之间相关性较低;2)所有特征具有相同的方差
\[x_{PCAwhite,i}=\frac{x_{rot,i}}{\sqrt{\lambda_i}} \]其中,\(x_{rot}\)为PCA处理后的数据,\(\lambda\)为PCA处理后数据的协方差矩阵对角元素。PCA白化实际是在PCA基础上进一步的数据处理,PCA使得特征间相关性降低,白化使得每个输入特征方差为1。
另外还有ZCA白化等,参见白化-UFLDL
![]()
上图为去相关和白化的处理效果。
初始化
在标准化输入数据之后,有充足理由假设,训练得到的参数一半为正,一半为负。为了减小训练成本,在初始化时,就应该让参数符合这一假设。但是应注意,全0初始化是不可取的。因为如果参数\(W\)初始化为0,则对于任何输入\(x_i\),隐藏层中每个神经元的输出都是相同的。这样即使梯度下降,无论训练多少次,这些神经元都是对称的,无论隐藏层内有多少个结点,都相当于在训练同一个函数。 即没有非对称的来源。参见什么时候可以将神经网络的参数全部初始化为0?、为什么神经网络参数不能全部初始化为全0?
实际上,初始化对神经网络来说是比较重要的内容,它甚至和梯度消失有关,已经有xavier、MSRA(He等)等初始化方法,参见神经网络中的梯度消失、深度学习中的初始化。在一些开源计算框架中已提供大量的参数初始化方式可供尝试,参见Module: tf.initializers-Tensorflow、初始化方法-Keras
训练中的Tricks
- 关于”size“的实践指南:
- 输入层的图片尺寸应是2的倍数
- 使用stride为1,filter size为\(3*3\),SAME padding的卷积层
- 使用\(2*2\)的池化层
- 学习率(Learning rate, LR)的实践指南:
- 一个典型的学习率大小:0.1,仅供一试 😃
- 使用验证集作为调节学习率的依据
- 如果在验证集上loss停止下降,调小学习率再继续训练(如将学习率除以2或除以5再继续)
激活函数
激活函数对神经网络影响巨大,因此出现了各种各样的激活函数,如sigmoid、tanh、ReLU、Leaky ReLU、Parametric ReLU(PReLU)、Randomized ReLU等。参见26种神经网络激活函数可视化
关于激活函数的实践指南:
- 使用ReLU,并注意学习速率的调整
- 试试Leaky ReLU / Maxout
- 试试tanh,但不要抱太大希望
- 不要使用sigmoid 😃
正则化
正则化是防止过拟合的手段之一。
在神经网络中,常见的正则化方法有:
- L2正则,将\(\frac{\lambda}{2n}\sum_{i=0}^{n}w_i^2\)加入损失函数中。其中,\(\lambda\)为正则化系数,\(w\)为神经网络的参数
- L1正则,将\(\lambda\sum_{i=0}^n|w_i|\)加入损失函数中,同上。L1和L2正则有时会合起来用。L2正则倾向于降低参数范数的总和,L1正则使得参数稀疏。参见:L1正则化及其推导
- Max norm,\(||w_i||_2<c\),即把参数限制在固定常数之内
- Dropout,随机丢弃神经网络中的神经元,粗暴但有效。
- Batch Normalization,层归一化。本意在于解决“内部协变量漂移”(internal covariate shift)的问题,但也能起到一定正则化的作用。
一些开源计算框架已经提供相关的正则化方法,如Explore overfitting and underfitting-Tensorflow、tf.nn.l2_normalize-Tensorflow、tf.nn.batch_normalization-Tensorflow、tf.nn.dropout、正则化器的使用-Keras、BatchNormalization-Keras、核心层-Keras
发生过拟合还可以通过增加训练集大小,加入随机噪声,早停等手段避免。参见噪声层Noise-Keras、keras的EarlyStopping callbacks的使用与技巧
画图洞察数据
通过画图来观察训练情况,比如Tensorflow提供了Tensorboard输出训练中的信息,参见:06:Tensorflow的可视化工具Tensorboard的初步使用
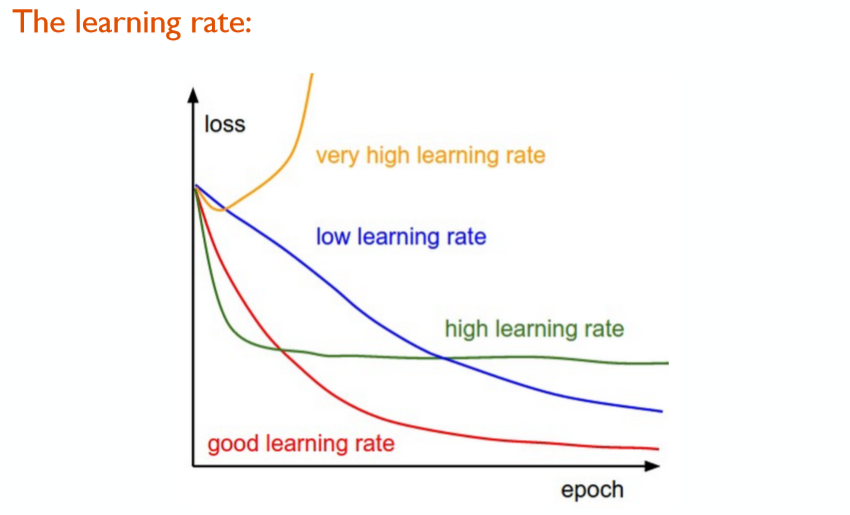
上图展示了,通过观察训练中的loss,来判断当前的学习速率是否适当。
- 如果loss曲线看起来太直,则学习率偏低
- 如果loss曲线下降太少,则学习率有可能偏高
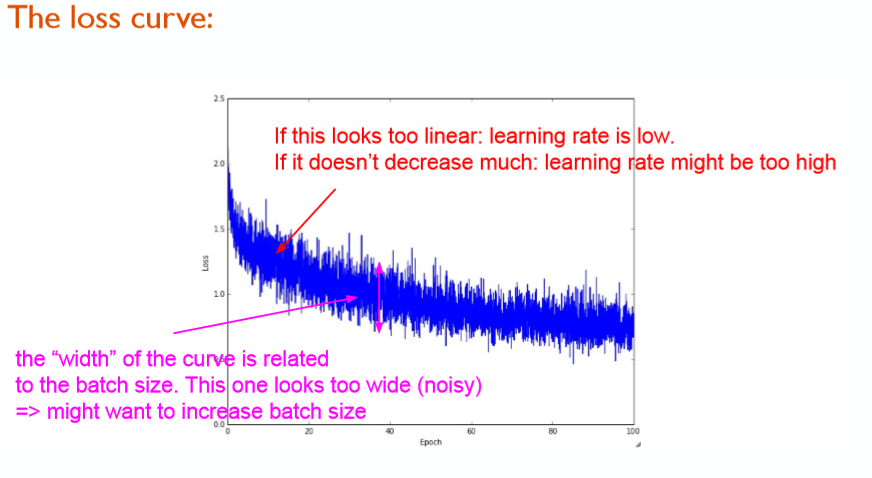
上图依然是展示训练中loss的变化。
loss曲线如果“过宽”,也即是loss曲线发生抖动,则说明batch_size设置过小。
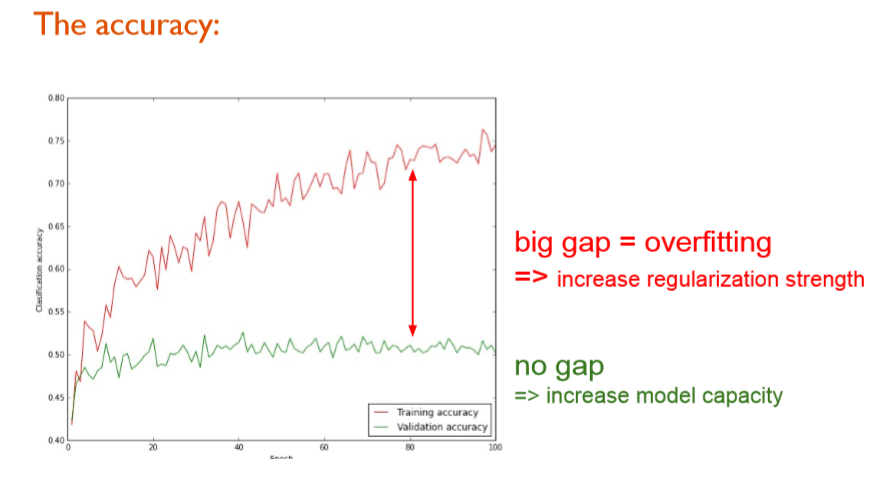
上图是训练集和验证集上正确率曲线,其中红色为训练集正确率,蓝色为验证集正确率。如果两者相差过大,则训练发生了过拟合,可以通过添加或加大正则化等手段避免过拟合。一般情况下,两者相差不大是我们希望看到的。


在图像中,可以通过输出第一个隐藏层观察正则化强度,如上图所示,两个第一隐层都充满着噪点,看不清图像,说明两者的正则化强度都不够高。第一隐层由于刚刚进入网络,还未进行“高度抽象”,所以观察到的图像应该是比较清晰的。
集成学习
集成学习是机器学习中通用的手段,在深度学习中,有一些特殊的集成学习Tricks:
- 同一模型,不同初始化。采用相同模型结构和超参数,但初始化不同,最后将所有模型的结果通过平均、投票等手段结合起来。
- 通过交叉验证(cross-validation, cv)获得模型的最优超参数
其它的集成学习方法如boosting, bagging, stacking, blending等参见一小部分机器学习算法小结: 优化算法、逻辑回归、支持向量机、决策树、集成算法、Word2Vec等的集成算法部分。
参考文献
Must Know Tips/Tricks in Deep Neural Networks (by Xiu-Shen Wei)
The Devil is always in the Details-Must Know Tips/Tricks in DNNs(PDF)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号