由声学特征重建语音波形-声码器的最近进展

本文介绍近期出现的、具有代表性的，由声学特征重建语音波形的相关工作。将声学特征转换为语音波形的这类模型通常被称作声码器，一般来说，目前的端到端语音合成首先由声学模型生成声学特征，比如梅尔频谱、线性谱等，再由声码器转换为最终的语音。生成语音中的韵律、表现力等由声学模型决定，而清晰度则由声码器决定，声码器限制了最终合成语音的音质，同时也是整个语音合成模型的计算瓶颈。

Efficient Neural Audio Synthesis

该文提出了一种使用双Softmax的单层循环神经网络WaveRNN用于波形重建。文中为了加快样本点生成速度和减小模型大小，展示了参数裁剪、子尺度（subscale）等技术。

代码地址：fatchord/WaveRNN

简介

序列模型的生成耗时分析

序列模型的生成时间\(T(u)\)是序列长度\(|u|\)和生成每一个样本点\(u\)耗费时间的乘积，而生成样本点\(u\)的时间又可以分为模型\(N\)个网络层/操作的计算时间\(c(op_i)\)和初始化时间\(d(op_i)\)：

\[T(u)=|u|\sum_{i=1}^N(c(op_i)+d(op_i)),\tag{1} \]

对于波形重建而言，序列长度\(|u|\)本身就很大，特别对于高质量的语音进行重建时，每秒包括24000个16bit位深的样本点。因此为了提高效率，可以通过：

1. 减少上式中的\(N\)，比如减少模型的层数，降低矩阵乘的次数。对于16bit的样本点，在WaveRNN中仅需要\(N=5\)个矩阵乘操作，相比之下，WaveNet包含30个残差模块，每个残差模块又包含2个网络层，每一个样本点需要\(N=30\times 2=60\)个矩阵乘操作。

2. 减少上式中的\(c(op_i)\)，比如利用参数裁剪技术减少模型中的参数数量。在WaveRNN中通过参数裁剪（weight pruning）技术稀疏模型参数，在实验中发现，对于固定的参数数量，大的稀疏WaveRNN要显著优于小而密集的WaveRNN。

3. 减少上式中的\(d(op_i)\)，在WaveRNN中采用定制的GPU操作减少时间开销。

4. \(u\)生成的并行化，\(|u|\)固然不能减小，但在WaveRNN中采用了子尺度（subscaling）的生成技术。一个长度为\(L\)的向量折叠为\(B\)个长度为\(L/B\)的子向量，\(B\)个子向量依次生成，每一个都依赖于之前的子向量。子尺度技术使得在一个批次内能够同时生成多个样本点。实践中，每个子向量的生成仅需要很小的下文信息，不需要依赖遥远的未来信息，因此下一个子向量的生成，可以在上一个子向量生成过程开始的不久之后就进行。实验中，子尺度WaveRNN能够在每一步产生\(B=16\)个样本，而不会损失音频清晰度。

WaveRNN

卷积序列模型为了增大感受野，一般需要叠加很深的网络层。WaveRNN讲RNN的状态分为两个部分，分别用于预测16bit音频样本点更为重要的粗8位（8 coarse bits）\(c_t\)和较不重要的细8位（8 fine bits），每个部分都会馈送到相应的softmax层，细8位的预测要以粗8位为输入条件。也即：

\[x_t=[c_{t-1},f_{t-1},c_{t}]\\ u_t=\sigma(R_uh_{t-1}+I_u^*x_t)\\ r_t=\sigma(R_rh_{t-1}+I_r^*x_t)\\ e_t=\tau(r_t\circ (R_eh_{t-1})+I_e^*x_t)\\ h_t=u_t\circ h_{t-1}+(1-u_t)\circ e_t\\ y_c,y_f=split(h_t)\\ p(c_t)=\mathop{softmax}(O_2 \mathop{relu}(O_1y_c))\\ p(f_t)=\mathop{softmax}(O_4 \mathop{relu}(O_3y_f)),\tag{2} \]

每个音频样本点要生成16bit，如果直接使用softmax需要\(2^{16}\)个标签，WaveRNN将16bit分为两个部分，也就是粗8位\(c_t\)和细8位\(f_t\)，从而将输出空间压缩到\(2^8=256\)个值上。

由于\(f_t\)的值依赖于\(c_t\)，因此需要先计算\(c_t\)，注意到公式第1行中\(c_t\)既作为输入，公式第7行又作为了输出。这就是带有\(*\)的这些矩阵的屏蔽作用了，矩阵\(I\)其实是一个掩蔽矩阵（mask matrix），用于切断输入中的\(c_t\)和输出中的\(c_t\)的一切连接，最终作为输入的粗8位\(c_t\)仅仅与细8位\(f_t\)的状态\(u_t,r_t,e_t,h_t\)相连接，而不会在求\(c_t\)时，将\(c_t\)作为输入，因此上式中除了最后两个之外，其实都需要计算两遍。

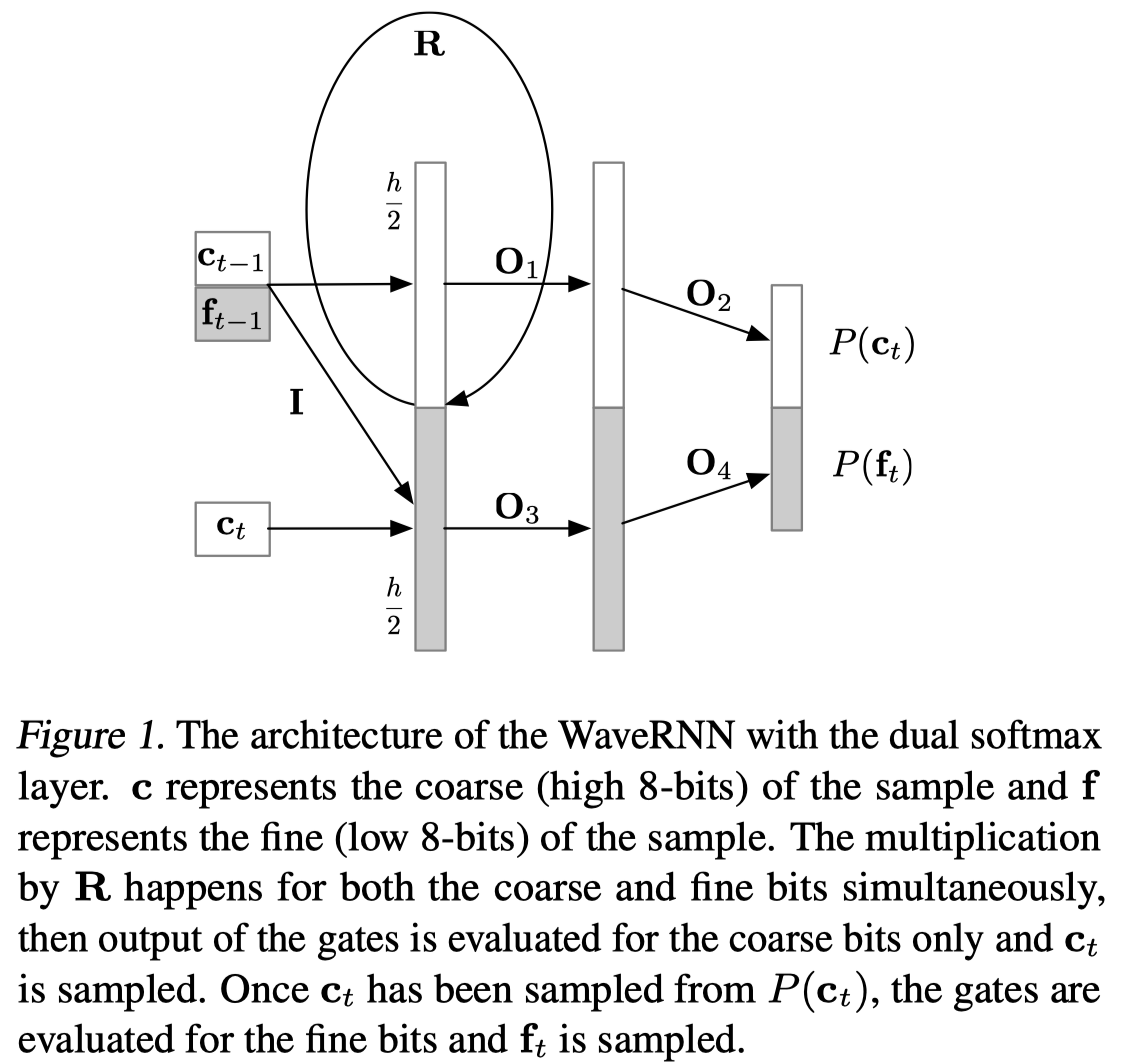
上图中，输入门首先从输出分布\(p(c_t)\)中采样出\(c_t\)，\(c_t\)被采样出来之后，\(f_t\)才能被计算和采样出来。注意，上图中的\(c_t\)并没有作为\(p(c_t)\)的输入。

Sparse WaveRNN

1. 参数稀疏方法

为了降低模型大小和提高生成速率，必须减小模型的参数量。通过实验发现，在同样参数量的情况下，大而参数“稀疏”的模型要比小而参数“密集”的模型效果好得多。所谓参数“稀疏”是指在参数矩阵中，值为0的参数比较多，WaveRNN采用权重裁剪方法的方法减少模型中的非零权重。具体的做法是，对每一个参数矩阵都维护一个二元掩蔽（binary mask）矩阵，开始时二元掩蔽矩阵的元素值全为1，每训练一段时间，就会对参数矩阵的元素进行排序，将参数矩阵值最小的\(k\)个元素对应的mask置为0。

\(k\)的计算需要考虑想要的稀疏度\(Z\)和参数矩阵中的元素总量，因此想要计算一个比例\(z\)，这个比例\(z\)乘上参数总量就是\(k\)的值，在训练过程中，从0开始逐渐增加到目标稀疏度\(Z\)，比例系数\(z\)的计算公式如下：

\[z=Z(1-(1-\frac{t-t_0}{S})^3) \]

其中，\(t\)为此时的训练步数，\(t_0\)为参数裁剪开始时的训练步数，\(S\)是总的裁剪步数。在该文的实验中，设置\(t_0=1000,S=200k\)，共训练\(500k\)步。文中使用该策略稀疏GRU单元的3个门矩阵。

同时，还可以通过编码稀疏矩阵的方法提高计算效率。该文发现，对于非结构化稀疏而言，\(m=16\)的参数块仅牺牲很小的表现，就能将稀疏矩阵所需的内存占用降低到\(\frac{1}{m}\)。（注：这里有点不懂，这是什么原理？）实验中分别采用了\(4\times 4\)和\(16\times 1\)块，后者有更高的生成速率。

2. 子尺度WaveRNN

如果可以一次同时生成多个样本点，就可以“减小”序列长度，就是一个并行生成的概念。这里一次生成\(B\)个样本点，因此序列长度就“缩小”了\(B\)倍：

\[T(u)=\frac{|u|}{B}\sum_{i=1}^N(c(op_i^B)+d(op_i^B)) \]

注意，这实际上并不代表着生成过程直接降低了\(B\)倍，因为每个批次的生成在一开始是串行生成的，只不过后续的批次只需要在前面批次开始生成后不久，就可以执行生成了。

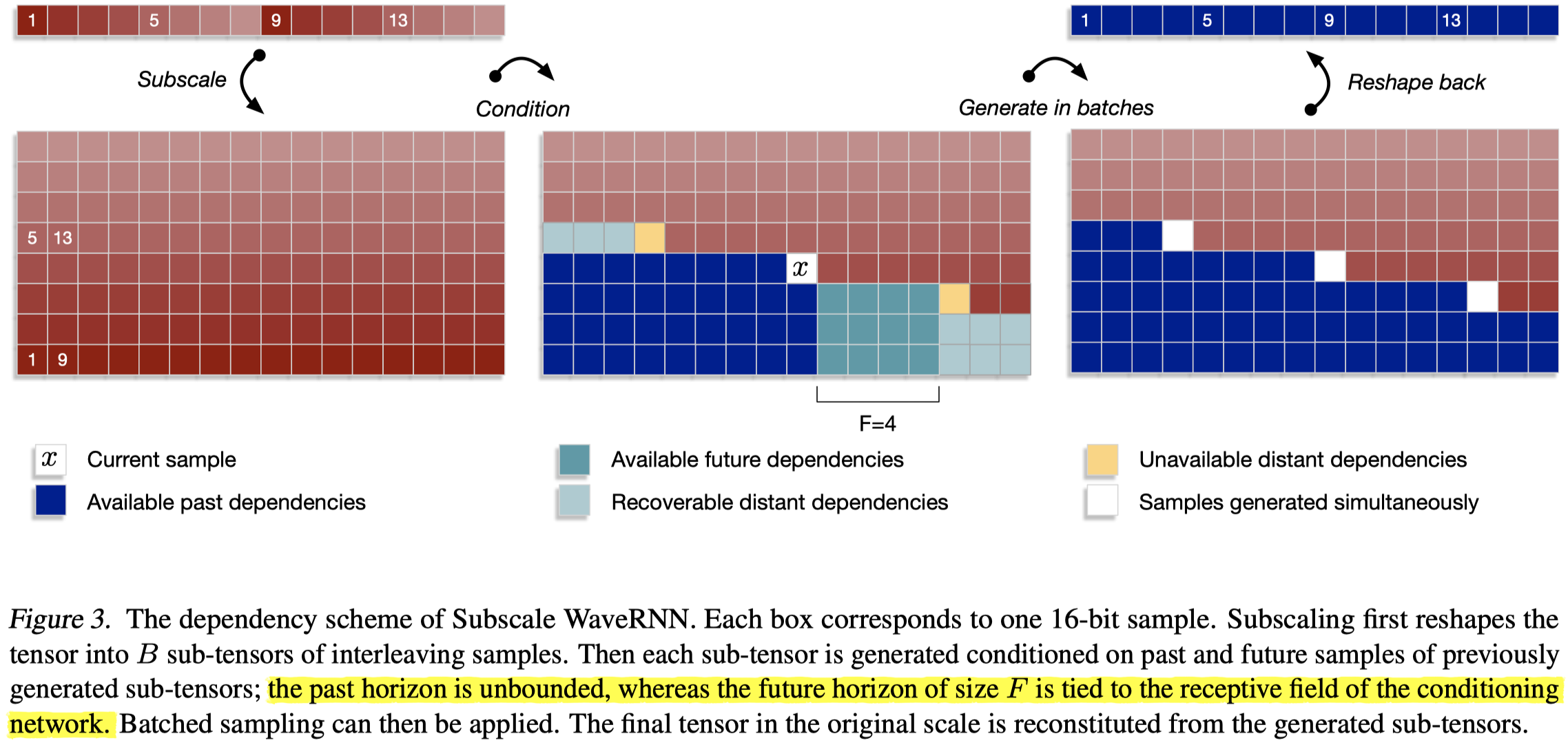
如上图，每个方块表示一个16bit样本点，白色方块表示正在生成的样本点。在中间一幅图中，蓝色方块表示已经生成的，用于指导当前样本点\(x\)生成的历史样本点；浅蓝色方块表示已经生成的，用于指导当前样本点\(x\)生成的未来样本点；最浅蓝色方块表示已经生成的，远距离的未来样本点。可以用于指导当前样本点生成的历史样本点是几乎没有限制的，而未来样本点的多寡与条件网络的感受野有关，图中以感受野大小\(F\)示意了这层关系。此外，注意图中样本点的折叠方式，有数字1、5、9、13示意了折叠后的顺序，列从下至上是样本点的真实排列顺序，行从左至右是当前样本点的索引值+8的未来样本点。

从图中可以发现，当前样本点的生成不仅仅依赖于之前的样本点，而且还会依赖未来的样本点，生成样本点的概率分布可以表示如下：

\[P(u)=\prod_{s=0}^{B}\prod_{i=0}^{|u|/B}P(u_{B_{i+s}}|u_{B_{j+s}}\ for\ j<i,\\ u_{B_{k+z}}\ for\ k\geq 0\ and\ z<s) \]

在上式中，样本点\(u_{B_{i+s}}\)依赖于之前\(z<s,k\geq 0\)的所有样本点\(u_{B_{k+z}}\)。样本点\(u\)的生成过程是：首先生成第一个子向量；之后以第一个子向量为条件，生成第二个子向量；第三个子向量之前两个子向量为条件，以此类推。

Parallel WaveGAN: A Fast Waveform Generation Model based on Generative Adversarial Networks with Multi-resolution Spectrogram

Parallel WaveGAN是一种利用生成对抗网络（Generative Adversarial Networks，GAN）无需蒸馏、快速、小型的波形生成方法。在该模型中，使用联合优化的多尺度频谱和对抗损失函数训练非自回归“WaveNet”。

代码地址：kan-bayashi/ParallelWaveGAN

简介

基于GAN的并行波形生成

GAN是一种利用两个神经网络进行对抗升级的训练策略，一般包括两个模块：生成器\(G\)和判别器\(D\)。和原始的WaveNet相比，该文中的Parallel WaveGAN（PWG）的生成器有以下的不同：

1. 使用非因果卷积；

2. 使用从高斯分布采样的随机噪声作为输入；

3. 在训练和推断阶段，该模型都采用的是非自回归模式。

Parallel WaveGAN（PWG）基于稳定性的考虑，采用最小二乘GAN（least-squares GANs）。Parallel WaveGAN（PWG）的生成器努力学习真实波形的分布，最终以假乱真，能够让判别器将生成波形误判为真实的。也即是最小化以下的对抗损失函数：

\[L_{adv}(G,D)=\mathbb{E}_{z\sim N(0,I)}[(1-D(G(z)))^2],\tag{1} \]

其中，\(z\)为输入白噪声。上式为了简洁，将\(G\)的辅助部分省略掉了。

另一方面，判别器需要学习学习判定出真实音频，而区分出生成音频。也就是，使用的优化准则为：

\[L_D(G,D)=\mathbb{E}_{x\sim p_{data}}[(1-D(x))^2]+\mathbb{E}_{z\sim N(0,I)}[D(G(z))^2],\tag{2} \]

其中，\(x\)和\(p_{data}\)分布表示目标波形和分布。

多尺度短时傅里叶变换辅助损失（Multi-resolution STFT auxilliary loss）

为了适用波形生成的需要，提出了多尺度短时傅里叶变换辅助损失。定义单个的短时傅立叶变换损失（STFT loss）：

\[L_s(G)=\mathbb{E}_{z\sim p(z),x\sim p_{data}}[L_{sc}(x,\hat{x})+L_{mag}(x,\hat{x})],\tag{3} \]

其中，\(\hat{x}\)表示生成样本，也即\(G(z)\)，\(L_{sc}\)表示谱收敛（spectral convergence）损失，\(L_{mag}\)表示对数短时傅里叶变换幅度（log STFT magnitude）损失，分别定义如下：

\[L_{sc}(x,\hat{x})=\frac{||\ |STFT(x)|-|STFT(\hat{x})|\ ||_F}{|\ ||STFT(x)||\ |_F}, \\ L_{mag}(x,\hat{x})=\frac{1}{N}||\ \mathop{log}|STFT(x)|-\mathop{log}|STFT(\hat{x})|\ ||_1,\tag{4} \]

其中，\(||\cdot||_F\)表示Frobenius范数，就是矩阵元素的平方和再开方：

\[||A||_F=\sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n}|a_{ij}|^2} \]

\(||\cdot||_1\)为L1范数：

\[||A||_1=\sum_{i=1}^{n}|a_i| \]

\(|SFTF(\cdot)|\)表示短时傅立叶变换的幅度值，\(N\)表示幅度值的元素个数。

该文中所谓的多尺度傅立叶变换损失，就是使用不同分析参数（比如傅立叶变换时的傅立叶变换大小FFT size，窗大小window size，帧移frame shift）的多个单短时傅立叶变换损失。假设有\(M\)个单短时傅立叶变换损失，则多尺度短时傅立叶变换辅助损失（\(L_{aux}\)）定义为：

\[L_{aux}(G)=\frac{1}{M}\sum_{m=1}^{M}L_s^{(m)}(G)\tag{6} \]

在基于傅立叶变换的时域信号表示中，时域分辨率和频域分辨率总是鱼与熊掌不可兼得，比如增加窗长会提高频域分辨率，而降低时域分辨率。通过结合不同分析参数下的多个短时傅立叶变换损失，可以帮助生成器学习语音的时域特性。此外，其也防止生成器对固定短时傅立叶变换的表示过拟合，能够有效地提高整个生成波形的最终表现。

因此，最终的生成器损失就是多尺度短时傅立叶变换损失和对抗损失的线性组合：

\[L_G(G,D)=L_{aux}(G)+\lambda_{adv}L_{adv}(G,D).\tag{7} \]

其中，\(\lambda_{adv}\)是平衡两个损失项的超参数。

实验语料

实验中使用24kHz，位深16bit的音频，11449句话，23.09小时。80维对数梅尔频谱（80-band log-mel spectrogram）作为输入的声学特征，梅尔频谱的频域范围为70-8000Hz，帧长50ms，帧移12.5ms，在训练之前将梅尔频谱规范化到0均值单位方差上。

实验细节

实际实现上，Parallel WaveGAN包含30个扩展残差卷积层，3个指数级扩展周期。残差和跳连的通道数设置为64，卷积核大小设置为3。判别器包含10个非因果扩展一维卷积，采用leaky ReLU激活函数（\(\alpha=0.2\)），步长设置为1，并且除了第一层和最后一层，一维卷积的扩展数线性增加，范围为\([1,8]\)。生成器的通道数、卷积核大小和判别器保持一致。对于判别器和生成器中的所有卷积层，均进行权重归一化（weight normalization）。

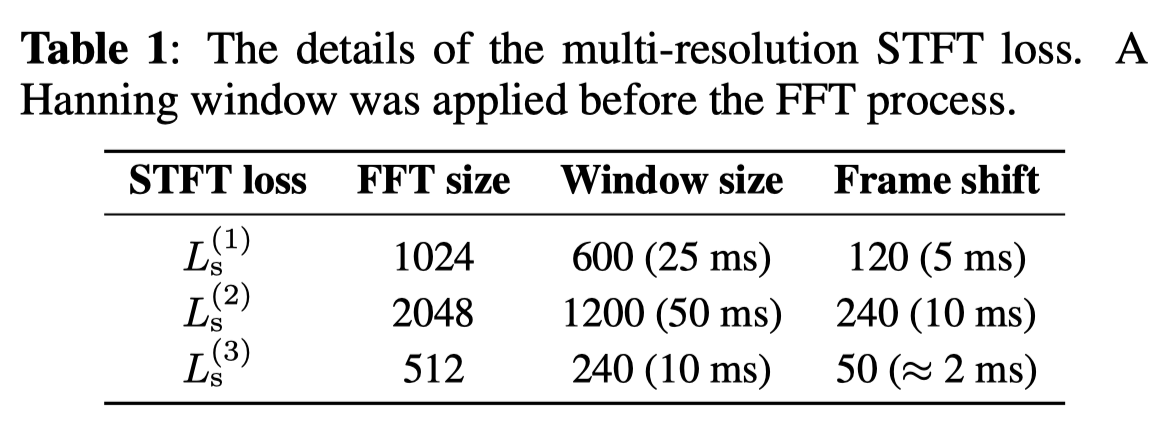
如上表，多尺度短时傅里叶变换损失是上表中三组分析参数计算出的单损失之和。经过实验验证，公式7中的超参数\(\lambda_{adv}\)设置为4.0。判别器在初始的100k步时固定，其后判别器和生成器联合训练。batch size设置为8，每一个音频片段剪裁到24k个样本点（1秒）。该模型通过上采样和二维卷积，使得声学特征的时间分辨率能够匹配语音波形的采样率。注意，声学特征并没有用于判别器。

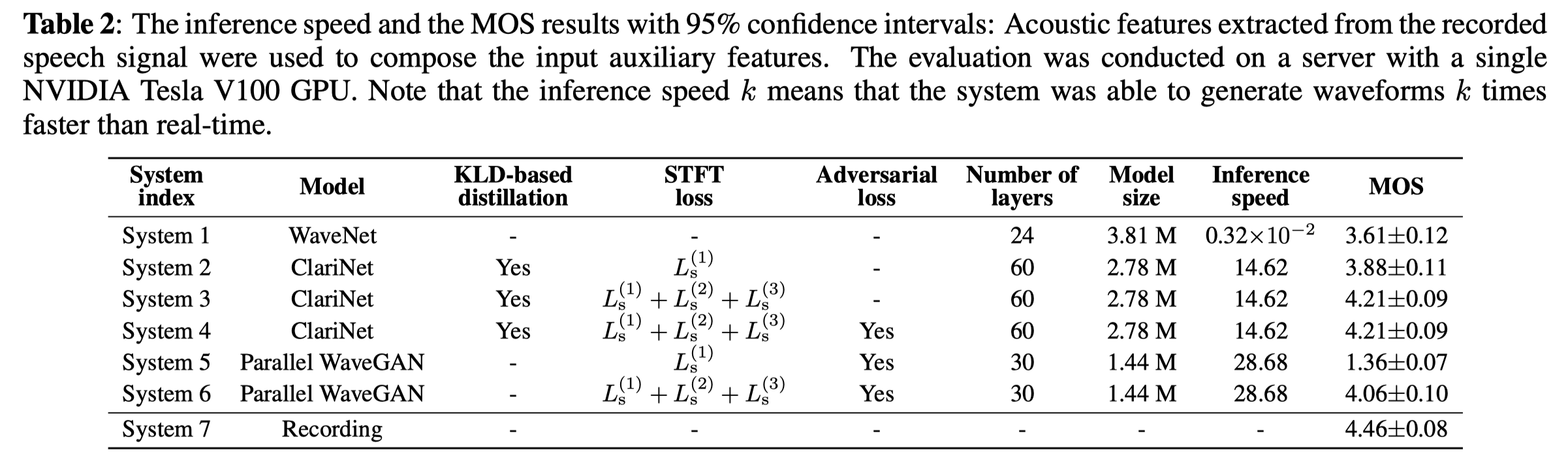
如上表是Parallel WaveGAN与其它基线模型的生成速度和MOS得分。

如上表是Parallel WaveGAN与其它基线模型的训练时间比较，所有模型均使用两卡V100训练。

MelGAN: Generative Adversarial Networks for Conditional Waveform Synthesis

MelGAN采用非自回归前馈卷积架构，在不引入额外蒸馏和感知损失的前提下，依然能够产生高质量的语音，是第一种利用生成对抗网络（Generative Adversarial Networks，GANs）合成时域波形的方法。由于模型计算复杂度低，并行度高，因而合成速度极快。

代码地址：

• descriptinc/melgan-neurips (official)

• seungwonpark/melgan

• kan-bayashi/ParallelWaveGAN

• rishikksh20/melgan

简介

由于MelGAN是基于GAN的生成模型，因而主要由生成器和判别器组成。生成器输入语音的压缩表示，如梅尔频谱，经过一层卷积后送入上采样层，上采样将梅尔频谱的序列长度匹配波形的频率。每次上采样都嵌套残差模块，最后经过一个卷积层获得音频输出。由于所要生成音频的声道数为1，因此最后一个的卷积层通道数也为1。对于判别器，主体是由卷积层和下采样层组成，并且采用多尺度架构，也就是不但对原始音频做判别，还将降频处理之后的音频馈送到判别器中进行判断，这里的降频采用平均池化的方法。MelGAN选择基于分组卷积的判别器，并使用所允许的最大卷积核，保持较小参数量的同时，捕获音频帧之间的相关性。

判别器和生成器具体的损失函数为：

\[\mathop{min}_{D_k}(\mathbb{E}_x[(D_k(x)-1)^2]+\mathbb{E}_{s,z}[D_k(G(s,z))^2]),\tag{1} \]

其中，\(D_k\)是第\(k\)个判别器，\(K\)为判别器的数量，\(x\)表示原始波形，\(s\)梅尔频谱，\(z\)表示高斯噪声向量。

\[\mathop{min}_G(\mathbb{E}_{s,z}[\sum_{k=1}^K(D_k(G(s,z))-1)^2]+\lambda \sum_{k=1}^K L(G,D_k)),\tag{2} \]

其中，

\[L(G,D_k)=\mathbb{E}_{x,s}[\sum_{i=1}^T\frac{1}{N_i}||D_k^{(i)}(x)-D_k^{(i)}(G(s))||_1],\tag{3} \]

\(L(G,D_k)\)是特征匹配损失，\(D_k^{(i)}\)是第\(k\)个判别模块的第\(i\)层的特征图输出，\(N_i\)是每一层的单元数，\(||\cdot||_1\)是L1范数。

最终MelGAN的训练目标为：

\[\mathop{min}_G(\mathbb{E}_{s,z}[\sum_{k=1}^K(D_k(G(s,z))-1)^2]+\lambda\sum_{k=1}^KL(G,D_k)).\tag{4} \]

Multi-band MelGAN: Faster Waveform Generation for High-Quality Text-to-Speech

多频带MelGAN将Parallel WaveGAN中的多尺度短时傅里叶变换损失（multi-resolution STFT loss）引入到MelGAN中，并且在音频的多个子带上分别度量损失。

代码地址：

• kan-bayashi/ParallelWaveGAN

• rishikksh20/melgan

简介

尽管使用的特征匹配损失可以稳定整个网络的训练，但无法有效衡量真实和预测音频之间的差异，因此引入了类似于Parallel WaveGAN的多尺度短时傅里叶变换损失（multi-resolution STFT loss）。对于单短时傅里叶变换损失，最小化真实音频和生成音频的谱收敛（spectral convergence）\(L_{sc}\)和对数短时傅里叶变换的幅度值（log STFT magnitude）\(L_{mag}\)：

\[L_{sc}(x,\widetilde{x})=\frac{||\ |STFT(x)-STFT(\widetilde{x})|\ ||_F}{||\ |STFT(x)|\ ||_F},\tag{5} \]

\[L_{mag}(x,\widetilde{x})=\frac{1}{N}||\mathop{log}|STFT(x)-\mathop{log}|STFT(\widetilde{x})|\ ||_1.\tag{6} \]

其中，\(x\)是真实音频，\(\widetilde{x}\)是生成器\(G(s)\)输出的预测音频，\(||\cdot ||_F\)和\(||\cdot ||_1\)表示Frobenius和L1范数，\(|STFT(\cdot)|\)表示短时傅里叶变换，\(N\)是幅度谱的元素个数。

对于多尺度短时傅里叶变换目标函数，有\(M\)个不同分析参数的单短时傅里叶变换损失，加和平均这些单个损失：

\[L_{mr\_stft}(G)=\mathbb{E}_{x,\widetilde{x}}[\frac{1}{M}\sum_{m=1}^M(L_{sc}^m(x,\widetilde{x})+L_{mag}^m(x,\widetilde{x}))],\tag{7} \]

对于全频带版本的MelGAN（FB-MelGAN），使用多尺度短时傅里叶变换损失替换特征匹配损失，因此最终的损失函数为：

\[\mathop{min}_G \mathbb{E}_{s,z}([\lambda \sum_{k=1}^K(D_k(G(s,z))-1)^2]+\mathbb{E}_s(L_{mr\_stft}(G))),\tag{8} \]

而对于多频带MelGAN（MB-MelGAN），同时在全带和各个子带尺度上应用多尺度短时傅里叶变换损失：

\[L_{mr\_stft}(G)=\frac{1}{2}(L_{fmr\_stft}^{full}(G)+L_{smr\_stft}^{sub}(G)),\tag{9} \]

其中，\(L_{fmr\_stft}^{full}\)和\(L_{smr\_stft}^{sub}\)分别表示多尺度短时傅里叶变换损失的全频带和子频带版本。

MB-MelGAN使用一个生成器生成所有子带的信号，共享的生成器以梅尔频谱作为输入，同时预测所有子带的信号以用于多尺度短时傅里叶变换的计算。具体的训练方法如下。

1. 初始化\(G\)和\(D\)的参数。

2. 如果是FB-MelGAN，使用公式7中的\(L_{mr\_stft}(G)\)预训练\(G\)，直至收敛；如果是MB-MelGAN，使用公式9中的\(L_{mr\_stft}\)预训练\(G\)，直至收敛。

3. 使用公式1训练\(D\)。

4. 使用公式8训练\(G\)。

5. 重复步骤3、4，直至\(G-D\)模型收敛。

在训练完成后，利用生成器\(G\)生成音频即可。

总结

可以看到，为了平衡生成速率和音质，近期的工作主要集中在利用生成对抗网络的改进上。WaveRNN能够取得较好的音质，但速度比较慢；Parallel WaveGAN和Multi-Band MelGAN可以在较短时间内合成较好的音频。目前的神经声码器已经可以实时生成波形。