简单四则运算题目生成与计算器

2018-03-20 21:34 mengmz 阅读(720) 评论(0) 编辑收藏举报

在自学构建之法-第二版这本书，读到第一章看到了这个题目，于是也想练一练手，遂有此记。

按照软件工程的要求，首先需要对项目进行时间预估，待完成后再填写实际花费的时间。

项目时间预估以及实际花费时间

PSP2.1	Personal Software Proces Stages	Time
Planning	计划
- Estimate	- 估计这个任务需要多少时间	40h
Development	开发
- Analysis	- 需求分析（包括学习新技术）	2h
- Design Spec	- 生成设计文档	1h
- Design Review	- 设计复审（和同事审核设计文档）	2h
- Coding Standard	- 代码规范（为目前的开发指定合适的规范）	0.5h
- Design	- 具体设计	10h
- Coding	- 具体编码	10h
- Code Review	- 代码复审	2h
- Test	- 测试（自我测试，修改代码，提交修改）	3h
Reporting	报告
- Test Report	- 测试报告	3h
- Size Measurement	- 计算工作量	0.5h
- Postmortem & Process Improvement Plan	- 事后总结，并提出过程修改意见	1h
	合计	35h

需求分析

1.生成满足一定要求的四则运算题目，并给出其答案；

1.1 能够识别控制参数
1.2 计算过程不产生负数
1.3 除法的结果为真分数
1.4 运算符数目限定为三个
1.5 生成的题目不能重复，即不能通过有限次+和x的交换律变为同一道题目
1.6 输出题目时对真分数要进行格式处理
1.7 生成题目的同时，计算出答案，并输出到文件
1.8 支持一万道题目的生成

2.对生成的题目的答案进行对错判定，统计对错数量；

设计开发

开发的过程有些曲折，作为半路出家程序员，实践能力确实缺乏，很长时间在抓脑袋，思来想去没有头绪。

开发第一版：我的想法

采用C++进行开发。直接按照需求，一个一个解决问题：

1.1

通过main(int argc, char* argv[])进行命令行参数的读取，随后编写一个parser解析出各个控制参数。需要注意的是，-r参数必须指定，它规定了四则运算数值的范围。

1.1.5

在完成后面需求之前，需要先生成一个随机表达式，然后再对其施加约束，当然1.4的约束可以在表达式生成时进行添加。

关于数值的表示方法

如果存在除法，则计算结果为真分数。

在一个随机生成的表达式中，存在自然数和真分数，处理这种混合表达式，如果采取自然数和真分数“先分别提取，再运算”的策略，无疑会引入额外的复杂操作。简单的处理方法是：将所有数值都当做真分数进行处理，建立MyFraction class ，为该类定义+、- 、x、÷运算；并且，在计算过程中始终存储为\(\frac{a}{b}\)的形式，只在输出到文件时将假分数转换为\(c\frac{a}{b}\)的形式。

关于随机数

在C++中，采用default_random_engine和uniform_int_distribution进行随机数的生成，前者定义一个随机数引擎，后者将其映射到给定范围内的一个均匀分布。在随机数生成中，还遇到了一个小坑，随机数生成的一个bug 记录了当时的情形。

有几点需要注意：

产生的数值是自然数还是分数？这需要进行随机判断，否则分数在表达式中的比例会大大增加，使得题目计算复杂，但内容单调。
由于随机数的特性（在调试时产生的序列始终相同），在调式完成、项目最终完成时，可将default_random_engine与系统时间函数进行绑定，即default_random_engine e(time(nullptr))。

如何为表达式添加括号？

其实在此之前，我并不觉得这个思路有什么问题。可以推测出，我的思路是直接生成中缀表达式，但是如何在中缀表达式中添加括号并进行括号匹配，成了一个很难解决的问题：是在每个位置随机生成括号？那如何处理括号的匹配问题？特别是后一个问题，让我的这种中缀表达式派感到了绝望。

开发第二版：如何解决？

在卡壳的同时，我也在网络上进行搜索，看别人写的博客，学习他们的处理方法。比如：

其中，轮子哥的文章以及第三个链接给了我很大的启发，让我发现了存在的问题并及时改进。简而言之，是先生成后缀表达式，随后对后缀表达式进行各种约束。

如何生成后缀表达式？

在轮子哥的代码中，一边生成后缀表达式，一边按实际的计算顺序将后缀表达式分段，在每个小的分段上，根据运算符的类别，对表达式进行处理。例如\(a b [op]\),

如果op=='+'或者op=='x'：对a和b进行字典序升序排序，最终实现的就是其文中所说的归一化，在这中条件下，如果两个表达式重复，将他们的后缀表达式转换为一个中间的最小表示，一定是相同的。
如果op=='÷'并且分母为0：此时的结果是无意义的。在轮子哥的文章中，遇到b==0的情况时，在生成运算符时排除÷；
如果op=='-'并且计算结果为负：调换左右子式，就满足了要求1.2

在我的实现中，我建立了一个arithmetric_expression class，其中保存tree_node，它储存表达式数的根节点。在构建表达式树的过程中，借鉴了Create Random Math Expression的方法：

string postfixExpression =""
int termsCount = 0;
while(weWantMoreTerms)
{
    if (termsCount>= 2)
    {
         var next = RandomNumberOrOperator();
         postfixExpression.Append(next);
         if(IsNumber(next)) { termsCount++;}
         else { termsCount--;}
    }
    else
    {
       postfixExpression.Append(RandomNumber);
       termsCount++;
     }
}

实际过程中，通过控制生成数的数目以及运算符的数目，可以保证表达式树的平衡。每次遇到插入运算符节点时，对其左右子式进行判断，满足1.2、1.5以及避免除零的要求。随后，对表达式树进行后序遍历，依旧根据\(a b [op]\) 中左右子式以及op的类别，判断左右子式是否要加括号，等到遍历至根节点时，即可获得完整的中缀表达式。需要注意：进行的是后序遍历，但把后序遍历转换为中缀表达式储存在了树节点内。

tree_node的节点定义如下：

struct tree_node
{
	tree_node(const MyFraction & f0 = { 0,1 }, wchar_t op0 = L'0', tree_node*left0 = nullptr, tree_node* right0 = nullptr) : value(f0), op(op0), left(left0), right(right0) 
	{
		exp = value.output_proper_fraction();
	};
	MyFraction value; //储存表达式计算结果
	wstring exp; //储存中缀表达式
	wchar_t op;  //储存运算符

	tree_node* left;
	tree_node* right;
};

至此，1.2~1.4全部实现。

参考文章：二叉树前序、中序和后序遍历的非递归实现

1.5

参考了轮子哥的文章，采用了set进行表达式存储，由于set值的唯一性以及表达式的归一化，可以避免产生重复问题。

1.6,1.7,1.8

针对MyFraction class，添加了format_output方法，如果是真分数，直接输出；若是假分数，进行转换；若分母为1，则为自然数，只输出分子即可。

可以看到，在表达式树后序遍历的过程中，一边产生中缀表达式，一边储存了中间的计算结果，因此直接取根节点的value值，就是表达式的结果。

关于支持10000道题目生成的问题，我看到博客中说，会出现中间结果的值范围超过int区间从而采用long long的情况，但在我的程序中未出现。

2

对生成的题目进行正误判定，由于已经获得了中缀表达式，故主要思路是将中缀表达式转为后缀，随后再对后缀表达式进行求值，利用数据结构中的stack可以方便实现。

参考文章：Parsing/Shunting-yard algorithm

结束了么？

看上去是结束了，但是有一点需要注意：运算符÷是非Ascii字符，如何对其进行操作和输出？

操作：使用标准库中的wstring进行储存，遍历和选择，与之相关的字符串输入流为wistringstream
输出：在将表达式输出到文档时，需要设置本地化策略 ，即wcout.imbue(locale(""))，以保证能够正确输出特殊字符。但在进行计数时，存在一个小问题，设置了imbue(local(""))的计数变量在超过999后，每隔三位数就添加一个,号，就是说，原来是1024变成了1,024，那么如何恢复本地化策略呢？使用wcout.imbue(locale("C"))即可，这就是默认的策略。

输出示例：

int exp_count = 1;
locale a("C"), b("");
for (const auto & item : expressions)
{
    wstring exp = get<0>(item);
    MyFraction result_for_check = infix_expression_solve(exp);
    output1.imbue(a);
    output1 << exp_count << ". ";
    output1.imbue(b);
    output1<< format_output(exp) << endl;
    output2 << exp_count << ". " << result_for_check << endl;
    exp_count++;
}

代码复审及测试

在开发过程中使用了google test，对MyFraction class的运算符操作以及arithmetric_expression class的中缀、后缀变换进行了测试，通过了全部测试用例。
当数值范围在100以内时，测试中遇到计算结果为负的情况，这是因为最大公约数的求解方法存在bug，虽然采用的是辗转相除法，但是忽略了最大公约数必须为正数这一定义。

性能测试

1.生成10000道数值限制为100的题目，未关闭sync_with_stdio

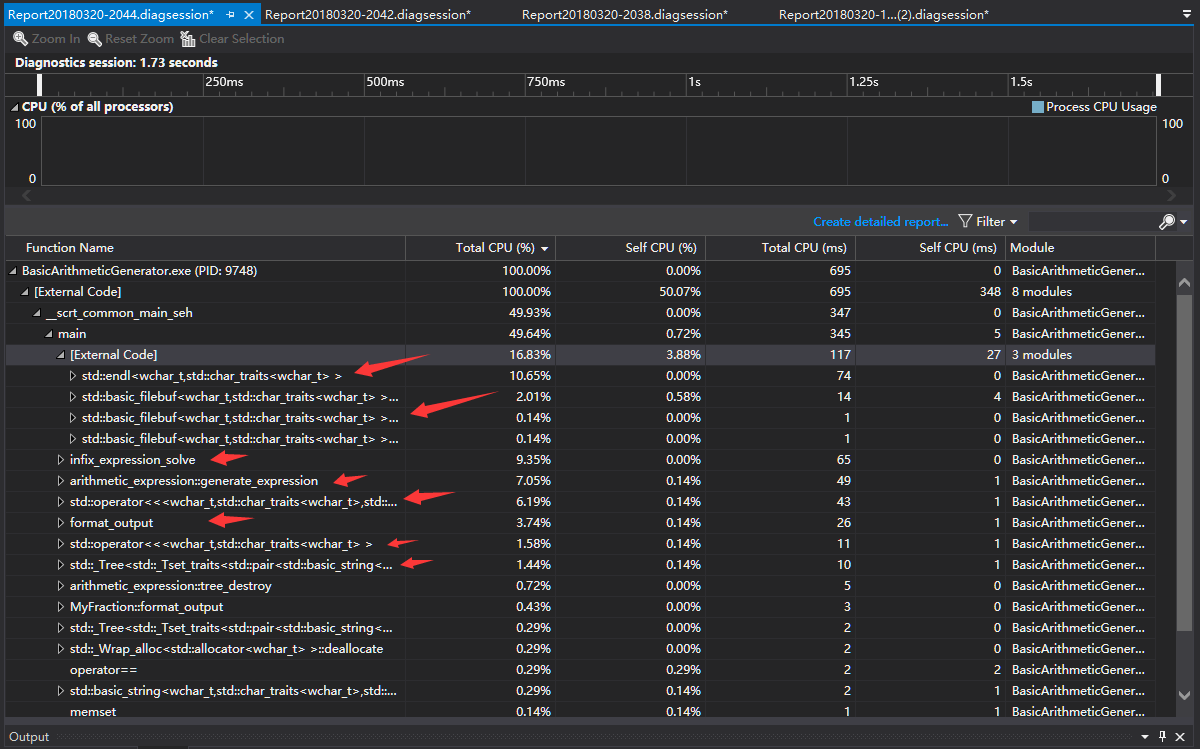
2.生成10000道数值限制为100的题目，关闭sync_with_stdio

可以看到：

关闭sync_with_stdio对endl、filebuf等旅游降低，但并不明显，当然这部分其实属于external code，并不受本文程序影响。
排名靠前的函数为generate_expression和infix_expression_solve，分别对应表达式生成和表达式结果的正误检测，是程序的核心所在。
输出占用了部分cpu。

3.生成50000道数值限制为100的题目，关闭sync_with_stdio

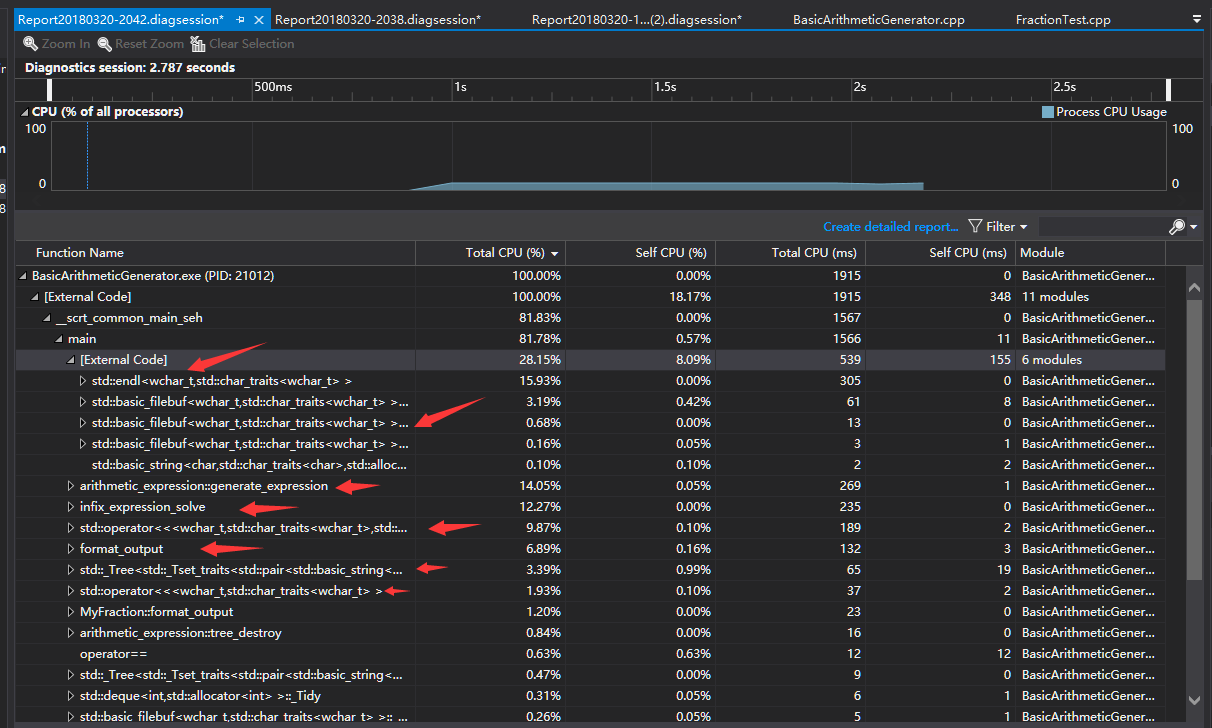
可以看到：

进程启动的cpu占用从50.07%降为18.17%，可以推测出进程启动所需的时间的是常量，随着运算规模的增大，所占用的比例会逐渐下降。
main中由于endl、filebuf等造成的cpu占用比例也有所降低。
其他函数的cpu占用保持一致。

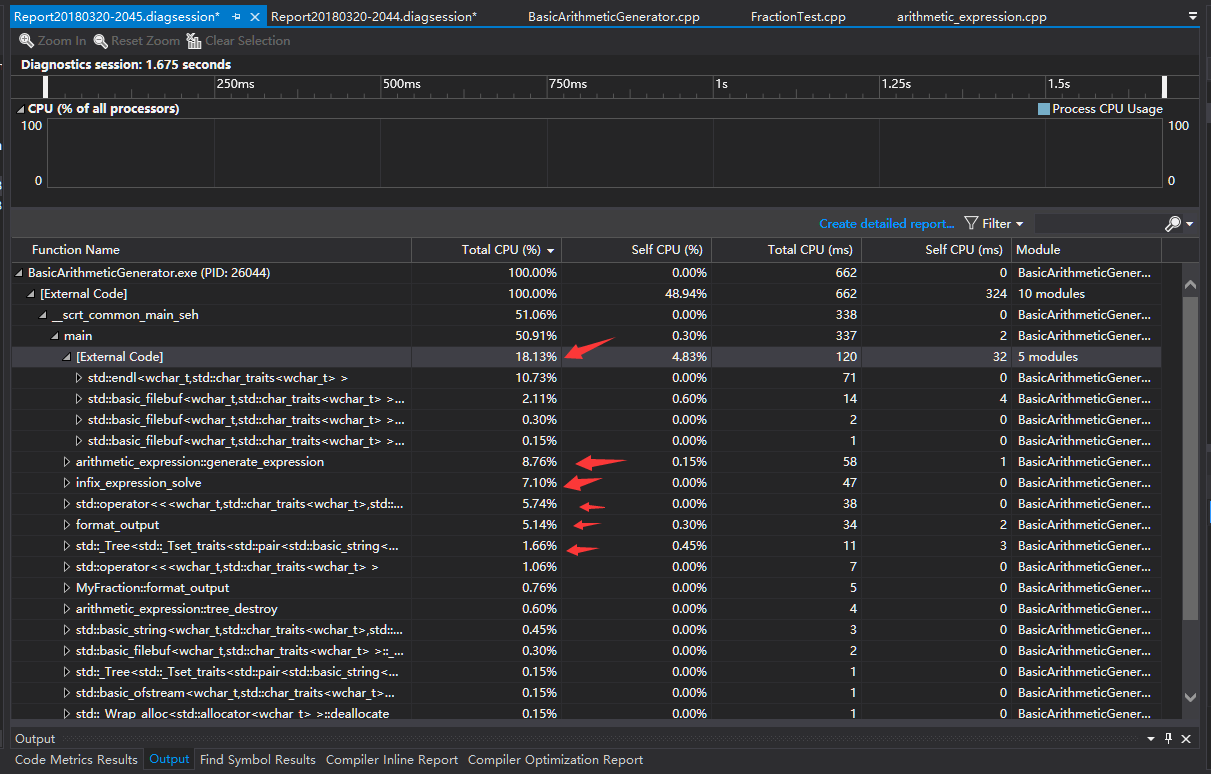
4.输出时调用imbue(locale(""))对于程序cpu占用的影响

在最开始的版本中，为了达到输出的要求，输出部分代码为：

 int exp_count = 1;
 for (const auto & item : expressions)
 {
     wstring exp = get<0>(item);
     MyFraction result_for_check = infix_expression_solve(exp);
     output1.imbue(locale("C"));
     output1 << exp_count << ". ";
     output1.imbue(locale(""));
     output1<< format_output(exp) << endl;
     output2 << exp_count << ". " << result_for_check << endl;
     exp_count++;
 }

进行性能测试时发现imbue占用了较大的cpu，推测是在每次for循环中，都要调用locale的构造函数创建新对象。于是，将代码改为了上文输出示例中的结果，在此测试发现imbue已经不再是cpu的显著占用者。

总结

至此，这个小项目暂时宣告结束。代码的重构、结构优化依然在进行，毕竟实现完美不太可能。

在这个过程中，感触最深的一点是：书中说阿超20分钟就完成了这个“软件”，但很惭愧，我花了两周才勉强搞定，而且还是翻看了许多前人博客的经验总结，特别是借鉴了轮子哥的代码，除了后缀表达式分割部分较复杂，我没有看懂外，其他部分的代码都读懂并再利用，其中数据结构的设计、函数功能的实现，乍看上去平淡无奇，不知所云，但实际上都非常精妙，承接前后。虽然只是稍微露了一手，但实在让我佩服不已，有了学习的榜样。

在这个项目中，最大的问题是没有计划好，比如第一次的设计方案并未经过仔细的推敲和论证，才导致“中缀表达式如何进行括号匹配”拦在路前，无法继续，最后不得不将方案推导，从头开始。

过后想一想，其实关键的地方在于表达式的中缀、后缀表示，表达式树的构建、中序和后序遍历，都与最基本的数据结构有关，这也说明了基础必须要打牢固，不然肯定要吃亏。

以后继续多动手实践，继续努力！

刷新页面返回顶部

mengmz