经典排序算法——选择排序

选择排序的原理

选择排序的原理是首先取第一个数字作为数组中的最小者minValue(以升序排序为例)，依次跟后续数字进行比较，如果发现有比minValue更小的数字，记录该数字的下标，并将该数字的值赋给minValue，直到遍历完数组的最后一个数字。然后根据记录的实际最小值的下标，跟第一个数字进行交换。

第一趟比较执行完后就找到了数组中最小者，然后再从下一个数字开始，重复执行前面的步骤，直到倒数第二个数字比较完为止(最后数字无需比较即为最大数字)

 图解选择排序过程

假设要排列的数字为 3 1 4 2 ，当进行第一趟排序时，如下图所示（其中i表示数组的下标）

第一趟排序后，数组中最小的数字1已找到并放置在第0位置。下面看第二趟比较，如下图所示。

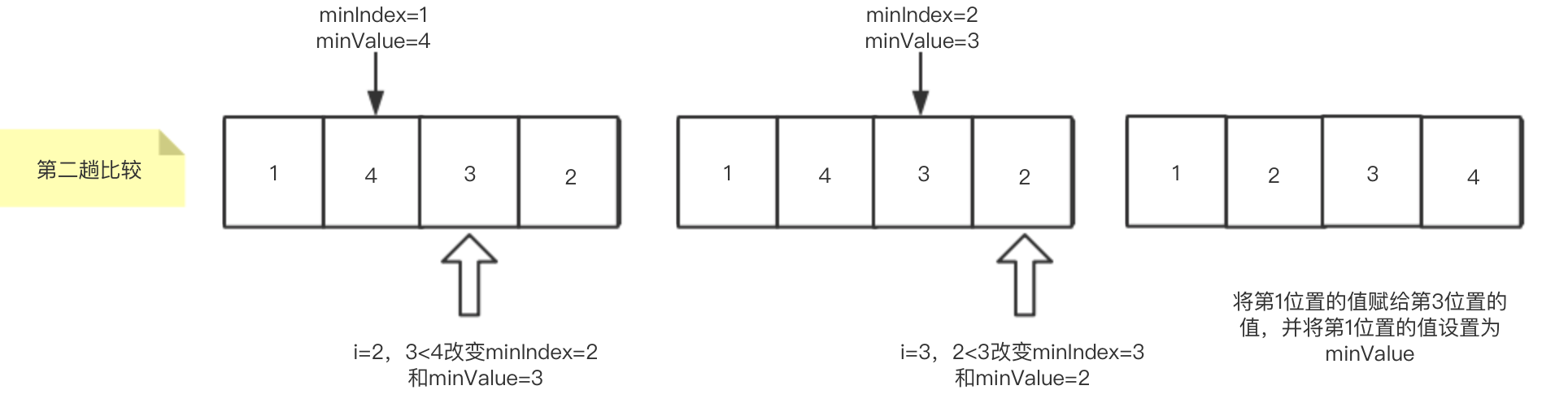
第二趟比较从第二个数开始，将minIndex设置为1，并将minValue设置为4。并依次跟后面的数比较，发现3<4，将minIndex和minValue修改为对应值。继续向后比较发现2<3，将minIndex和minValue修改为对应值。第二趟遍历结束，将第1位置的值设置为minIndex对应的值2，并将minIndex值设置为4。第二趟比较结束。继续执行第三趟排序(虽然我们看到现在数组已经有序，但程序不知道)。第三趟比较如下图所示

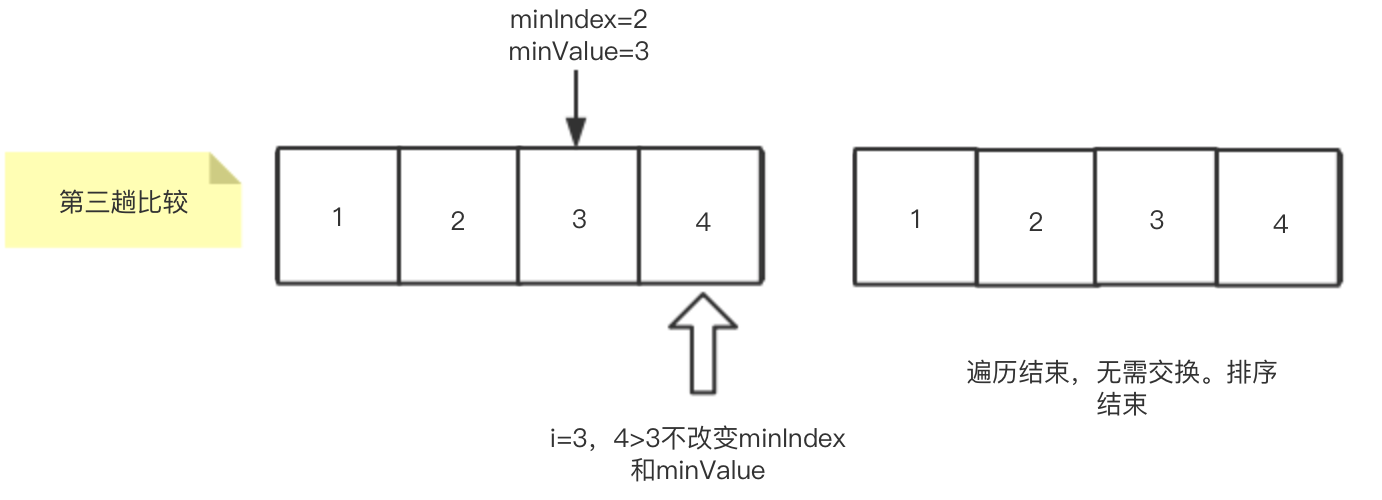
第三趟比较时，将minIndex设置为2，minValue设置为3。依次向后比较，4>3不改变minIndex和minValue。遍历结束，无需进行交换(通过趟数值与minIndex值是否相等来判断是否需要交换)

代码实现

public static void sort(int array[]){
        //第一个for循环表示要进行length-1次选择
        for (int i = 0; i < array.length - 1; i++) {
            int minIndex = i;
            int minValue = array[minIndex];
            for (int j= i+1; j<array.length; j++){
                if(minValue > array[j]){
                    minIndex = j;
                    minValue = array[j];
                }
            }
            //执行完一轮选择后进行交换(如果最小值下标有改变才进行交换)
            if(minIndex != i){
                array[minIndex] = array[i];
                array[i] = minValue;
            }
        }
    }

代码分析

1）第一层for循环确定比较趟数，通过我们的分析，比较n-1趟即可（n为数组长度）

2）第二层for循环用于遍历所选择的最小值后续数字，比较是否有小于所选择的最小值，如果有，则修改minIndex和minValue

3）if提交判断，用于判定minIndex是否被修改过，如果没有修改过，则无需交换(否则自己与自己交换，无意义)

时间复杂度

选择排序有两层for循环，所示时间复杂度为T(n)=O^2

测试执行时间

与上一篇冒泡排序相同，依然生成10万个数字进行排序。代码如下

public static void main(String []args){
        int array[] = new int[100000];
        for (int i = 0; i < 100000; i++) {
            array[i] = (int) (Math.random()*1000000);
        }
        long begin = System.currentTimeMillis();
        sort(array);
        System.out.println("总耗时="+(System.currentTimeMillis()-begin));
    }

执行结果（单位为毫秒）

 

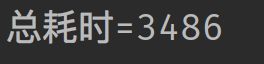
可以看出，在我的机器上使用选择排序对10万个数字的数组进行排序，大概需要3秒多的时间，比冒泡排序的17秒快了很多。下一篇我将讲解插入排序的过程，耗时会不会更小呢？一起期待！！！

总结

选择排序需要注意两点，一是比较的趟数，有n个数，比较n-1即可。二是每趟比较，都认为当前数为最小(或最大)值，然后依次跟后面数字比较，如果发现有比我们假设的最小值更小，则改变成新的下标和新的最小值继续向后比较，直到遍历完所有数字。如果假设的最小值下标有修改则进行交换。