B树和B+树

B树

一、基本原理

　　B树是一种查找树，它最初启发于二叉查找树。

　　二叉查找树的特点是每个非叶节点都只有两个孩子节点。然而这种做法会导致当数据量非常大时，二叉查找树的深度过深，搜索算法自根节点向下搜索时，需要访问的节点也就变的相当多。

　　如果这些节点存储在外存储器中，每访问一个节点，相当于就是进行了一次I/O操作，随着树高度的增加，频繁的I/O操作一定会降低查询的效率。

 

磁盘读取信息：

　　找到存储这个数据所对应的磁盘页面，这个过程是机械化的过程，需要依靠磁臂的转动，找到对应磁道，所以耗时长。

　　读取数据进内存，并实施运算，这是电子化的过程，相当快。

 

　　对于外存储器的信息读取最大的时间消耗在于寻找磁盘页面。那么一个基本的想法就是能不能减少这种读取的次数，在一个磁盘页面上，多存储一些索引信息。

　　B树的基本逻辑就是这个思路，它要改二叉为多叉，每个节点存储更多的指针信息，以降低I/O操作数。

 

二、基本结构

1. B树的定义

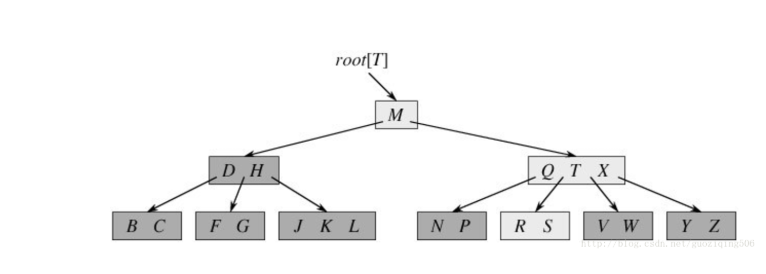
这里用最小度t来定义B树。一棵最小度为t的B树是满足如下四个条件的平衡多叉树：

• 每个节点最多包含2t−1个关键字；除根节点外的每个节点至少有t−1个关键字（t≤2），根节点至少有一个关键字；

• 一个节点u中的关键字按非降序排列：u.key1≤u.key2≤…u.keyn；

• 每个节点的关键字对其子树的范围分割。设节点u有n+1个指针，指向其n+1棵子树，指针为u.p1,…u.pn，关键字k为u.pi所指的子树中的关键字，有k1≤u.key1≤k2≤u.key2…成立；

• 所有叶子节点具有相同的深度，即树的高度h。这表明B树是平衡的。

 

一个标准的B树如下图：

 

 

三、搜索算法

一棵已经建立好的B树如下图所示，我们的目的是查找关键字为29的文件：

 

 

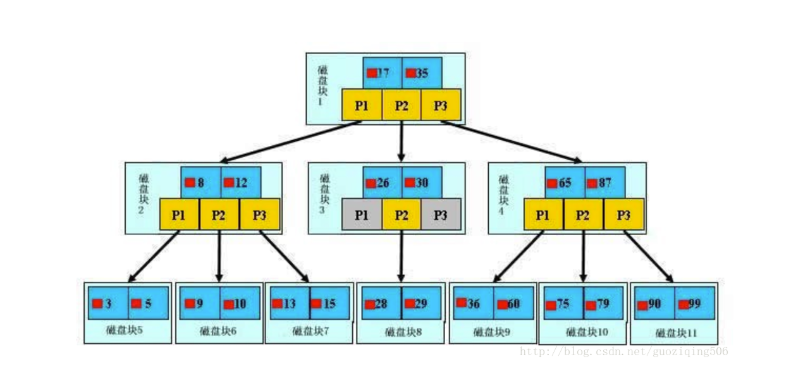
先简单对上图说明一下：

• 图中的小红方块表示对应关键字所代表的文件的存储位置，实际上可以看做是一个地址，比如根节点中17旁边的小红块表示的就是关键字17所对应的文件在硬盘中的存储地址。

• P是指针，不用多说了，需要注意的是：指针，关键字，以及关键字所代表的文件地址这三样东西合起来构成了B树的一个节点，这个节点存储在一个磁盘块上

下面，看看搜索关键字的29的文件的过程：

1. 从根节点开始，读取根节点信息，根节点有2个关键字：17和35。因为17 < 29 < 35，所以找到指针P2指向的子树，也就是磁盘块3（1次I/0操作）

2. 读取当前节点信息，当前节点有2个关键字：26和30。26 < 29 < 30，找到指针P2指向的子树，也就是磁盘块8（2次I/0操作）

3. 读取当前节点信息，当前节点有2个关键字：28和29。找到了！（3次I/0操作）

 

　　由上面的过程可见，同样的操作，如果使用平衡二叉树，那么需要至少4次I/O操作，B树比之二叉树的这种优势，还会随着节点数的增加而增加。

　　另外，因为B树节点中的关键字都是排序好的，所以，在节点中的信息被读入内存之后，可以采用二分查找这种快速的查找方式，更进一步减少了读入内存之后的计算时间。

 

 

B+树

B+树的定义

　　B+树是B树的一种变形，它更适合实际应用中操作系统的文件索引和数据库索引。

　　定义如下：（这里使用阶数m来定义B+树）

　　除根节点外的内部节点，每个节点最多有m个关键字，最少有⌈m/2⌉个关键字。其中每个关键字对应一个子树（也就是最多有m棵子树，最少有⌈m/2⌉棵子树）；

　　根节点要么没有子树，要么至少有2棵子树；

　　所有的叶子节点包含了全部的关键字以及这些关键字指向文件的指针

 

　　所有叶子节点中的关键字按大小顺序排列

　　相邻的叶子节点顺序链接（相当于是构成了一个顺序链表）

　　所有叶子节点在同一层

 

比如，下图就是一个非常典型的B+树的例子。

 

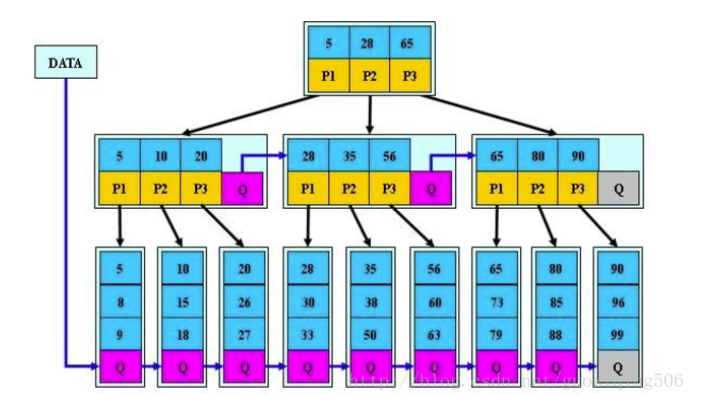
B+树和B树相比，主要的不同点在以下3项：

　　（1）B+树的非叶子节点不保存关键字记录的指针，这样使得B+树每个节点所能保存的关键字大大增加；

　　（2）B+树叶子节点保存了父节点的所有关键字和关键字记录的指针，每个叶子节点的关键字从小到大链接；

　　（3）B+树的根节点关键字数量和其子节点个数相等;

　　（4）B+的非叶子节点只进行数据索引，不会存实际的关键字记录的指针，所有数据地址必须要到叶子节点才能获取到，所以每次数据查询的次数都一样；

 

根据B+树的结构，我们可以发现B+树相比于B树，在文件系统，数据库系统当中，更有优势，原因如下：

B+树的磁盘读写代价更低 
　　B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说I/O读写次数也就降低了。

B+树的查询效率更加稳定 
　　由于内部结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

B+树更有利于对数据库的扫描 
　　B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题，而B+树只需要遍历叶子节点就可以解决对全部关键字信息的扫描，所以对于数据库中频繁使用的range query，B+树有着更高的性能。

 

参考：https://blog.csdn.net/guoziqing506/article/details/64122287