软考算法--N皇后问题

问题介绍:

简单来说,就是在nxn的棋盘上放置n个棋子,棋子两两之间不同行,不同列,不在同一斜线上.

放置过程:

首先每个棋子放置的位置都应满足不同列和不在同一斜线上.从第一行开始,先在第一行第一个位置放置一个,然后在下一行寻找合适的位置放置,第二行放好再放第三行,如果第三行没有合适的位置,那么就要更改第三行的上一行也就是第二行的位置,然后在尝试放置第三行,如此往下进行,某一行无法放置就改变上一行的位置,再重新尝试放置,直到n个都放置完毕,这样就形成一个解.这种方法就是回溯法.

4皇后的一个放置过程:

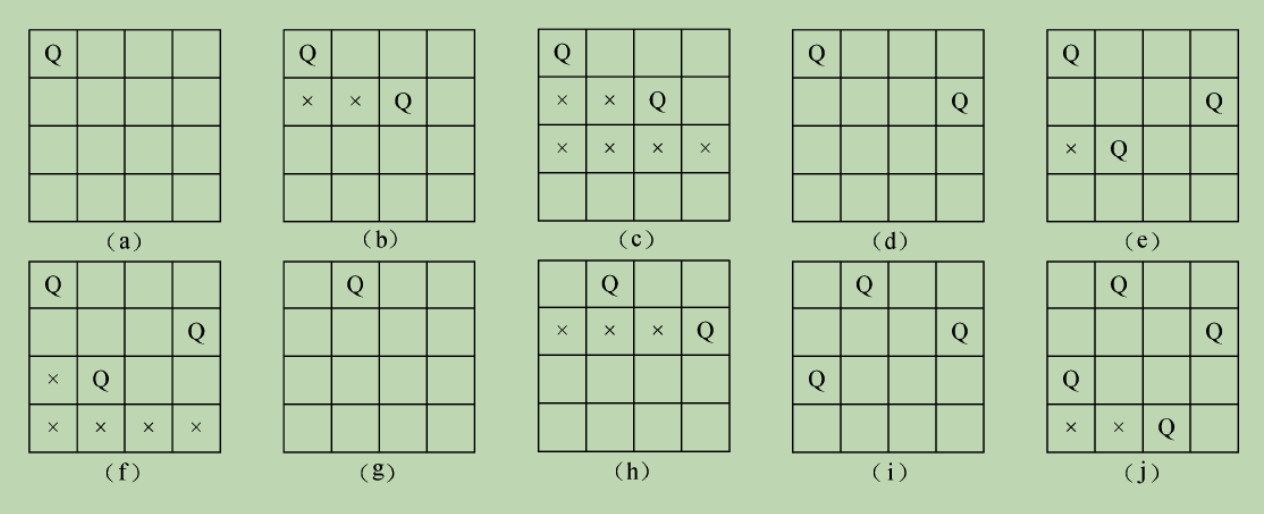
 代码(回溯法):

实现回溯的关键部分如下

void Nqueen(int j)
{
    for (int i = 1; i <= n; i++)
    {
        q[j] = i;
        if (check(j) == 1)//检查摆放位置是否合法
        {
            if (j == n)//都摆放完则输出
            {
                show();
            } else//否则继续摆下一个
            {
                Nqueen(j + 1);
            }
        }
    }
}

完整代码:

#include <stdio.h>
#include <stdlib.h>

#define n 4

int q[n + 1];//存储皇后的列号

int check(int j)//检查第j个皇后的位置是否合法
{
    for (int i = 1; i < j; i++)
    {
        //检查是否位于同列或同一斜线（列-列=行-行）
        if (q[i] == q[j] || abs(q[i] - q[j]) == abs(i - j))
        {
            return 0;
        }
    }
    return 1;
}

void show()//打印摆放结果
{
    printf("(");
    for (int i = 1; i <= n; i++)
    {
        printf(" %d", q[i]);
    }
    printf(" )\n");
}

void Nqueen(int j)
{
    for (int i = 1; i <= n; i++)
    {
        q[j] = i;
        if (check(j) == 1)//检查摆放位置是否合法
        {
            if (j == n)//都摆放完则输出
            {
                show();
            } else//否则继续摆下一个
            {
                Nqueen(j + 1);
            }
        }
    }
}

int main()
{
    Nqueen(1);
    return 0;
}

结果: