python习题-蒙特·卡罗法计算圆周率

【题目描述】

蒙特·卡罗方法是一种通过概率来得到问题近似解的方法，在很多领域都有重要的应用，其中就包括圆周率近似值的计问题。假设有一块边长为2的正方形木板，上面画一个单位圆，然后随意往木板上扔飞镖，落点坐标(x,y)必然在木板上（更多的时候是落在单位圆内），如果扔的次数足够多，那么落在单位圆内的次数除以总次数再乘以4，这个数字会无限逼近圆周率的值。这就是蒙特·卡罗发明的用于计算圆周率近似值的方法。编写程序，模拟蒙特·卡罗计算圆周率近似值的方法，输入掷飞镖次数，然后输出圆周率近似值。

【思路】

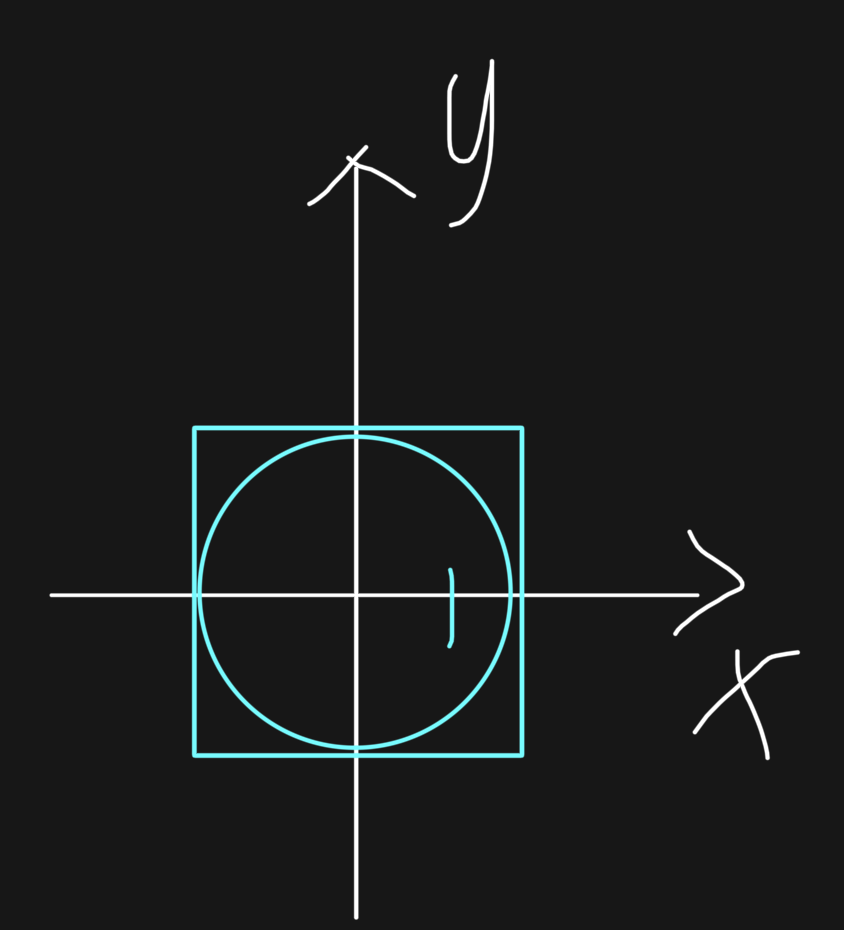
将题目看做下图，就是生成随机x，y，范围为（-1，1），再求x和y的平方和的平方根，小于1说明落在圆内。利用循环，循环n次，记录落在圆内的次数（x和y的平方和的平方根小于1的次数），再用题目里的式子求圆周率，这题不难

 

 

【源代码程序】

import math
import random

# 输入扔飞镖的次数n
n = int(input("输入扔飞镖的次数n:"))
count = 0
# 循环n次，每次生成两个范围为（-1，1）的小数并赋值给x，y
for i in range(n):
    x = random.uniform(-1, 1)
    y = random.uniform(-1, 1)
    # 求x,y的平方和的平方根
    c = math.sqrt(x ** 2 + y ** 2)
    # 如果c小于等于1，说明（x，y）落在单位圆里，次数加1
    if c <= 1:
        count += 1
print("落在单位圆内的次数为%s" % count)
# 落在单位圆内的次数除以总次数再乘以4，这个数字会无限逼近圆周率的值
pi = (count / n) * 4
print("圆周率近似为%s" % pi)

【运行测试】