被暴打的一天 居然爆出了15这种优秀的分数。
T1
在某些大佬嘴里 这是一道送分题。。然而蒟蒻爆零了。
这是大佬们显然出来的结论: \(a,b\)分别形成了两个连通块 两个连通块的交界处是\(+a,-b\) 那么接下来就只需要找到一条边,将这棵树分成两个大小分别为\(a,b\)的部分 找到这一条边之后就可用\(dfs,bfs\)随随便便由这条边向外扩展找到解了 无解的情况就是找不到一条边将这棵树分成两个大小分别为\(a,b\)的部分
这道题想到这个结论就真的很简单了 只有像我一样的蒟蒻会想到把点按照度排序,然后就不会了
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int maxn=100010;
int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
int n,a,b;
int first[maxn<<1],nxt[maxn<<1],to[maxn<<1],tot=1;
int bj,type,f[maxn],bh[maxn],size[maxn];
bool visit[maxn];
void add(int x,int y)
{
tot++;
nxt[tot]=first[x];
first[x]=tot;
to[tot]=y;
}
void dfs1(int x,int fa)
{
if(bj) return ;
size[x]=1;f[x]=fa;
for(int i=first[x];i;i=nxt[i])
{
int y=to[i];
if(y==fa) continue;
dfs1(y,x);
size[x]+=size[y];
}
if(size[x]==a)
bj=x,type=a;
else if(size[x]==-b)
bj=x,type=b;
}
void bfs1()
{
queue<int> q;
q.push(bj);
int wtf=(type==b)?b:a;
visit[bj]=true;
while(!q.empty())
{
int x=q.front();
q.pop();
bh[x]=wtf;
if(wtf<0) wtf++;
else wtf--;
for(int i=first[x];i;i=nxt[i])
{
int y=to[i];
if(y==f[x]) continue;
if(!visit[y])
{
visit[y]=true;
q.push(y);
}
}
}
while(!q.empty()) q.pop();
q.push(f[bj]);
visit[f[bj]]=true;
wtf=(type==b)?a:b;
while(!q.empty())
{
int x=q.front();q.pop();
bh[x]=wtf;
if(wtf<0) wtf++;
else wtf--;
for(int i=first[x];i;i=nxt[i])
{
int y=to[i];
if(visit[y]) continue;
visit[y]=true;
q.push(y);
}
}
}
int main()
{
n=read();a=read();b=read();b=-b;
for(int i=1,x,y;i<=n-1;i++)
{
x=read();y=read();
add(x,y);add(y,x);
}
bj=0;
dfs1(1,0);
if(bj==0) return printf("-1"),0;
bfs1();
for(int i=1;i<=n;i++)
printf("%d ",bh[i]);
return 0;
}
T2
第一眼:动规题 然后打了两个小时的动规 调试了半天和大样例不一样最后发现题目读错了 0分结尾 可能只有像我一样的蒟蒻才会以为括号里面不能有括号吧
标程是一个假的二维\(dp\)(第二维只有两个状态)
\(dp_{i,j}\)表示 当前第\(i\)位 前面有\(j\)个括号还没有被匹配
这里注意:如果前面有\(>=2\)个括号存在 那么里面的正负性一定是会被抵消的。因为两个括号的话相当于没有变化正负性
然而这种方法太过于复杂 因此可以用另一位大佬 的神奇思想A掉此题。
我们知道 如果在正数前面打括号 那么这个括号是毫无意义的
所以我们可以将连续的正数和在一起 这样对于处理过后的序列就只会有连续的一个+号了!
现在我们只讨论数字前面的符号:(显然如果第一个为加号的话可以直接跳过)
\(1.-a-b\) 我们总是可以用巧妙的办法使得 除了\(a\)为负数 \(b\)及\(b\)以后的数贡献全部为正 构造方法: \(-a-b+c==>-(a-(b+c))\) , \(-a-b-c==> -(a-b-c)\) 如此就可以保证后面的全部为正了!
\(2.-a+b\) 因为我们将所有连续的正数合并在了一起 因此下一个数必定有事负数 即\(-a+b-c\) 我们发现又出现了两个连续的负号 因此\(c\)及以后的所有数都会有正贡献 而提供负贡献的只有\(a,b\),其中\(a\)不论填不填括号都是负贡献 因此我们需要计算 b为正提供的贡献大 还是后面所有数提供的正贡献大
只有这两种情况。。。 然后接下来就可以枚举每一个负号的位置 判断当前是否要填括号
为了优化复杂度 我们需要预处理出前缀和 以及后面全部取正的后缀和
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
#define ll long long
using namespace std;
const int maxn=100010;
ll read()
{
ll x=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
ll sufsum[maxn],presum[maxn],maxx=0;
ll n,t,num[maxn],flag,tot,numm[maxn];
int main()
{
// freopen("sample3.in","r",stdin);
// freopen("jerry.out","w",stdout);
t=read();
while(t--)
{
n=read();
memset(numm,0,sizeof(numm));
for(register ll i=1;i<=n;i++)
num[i]=read();
flag=1;tot=0;
for(register ll i=1;i<=n;i++)
{
if(num[i]>0){
tot+=flag;
presum[tot]=presum[tot-flag]+num[i],flag=0;
}
else{
tot++;
presum[tot]=presum[tot-1]+num[i],flag=1;
}
}
ll tott=tot+1;flag=1;
sufsum[tott]=0;
for(register ll i=n;i>=1;i--)
{
if(num[i]>0){
tott-=flag;
sufsum[tott]=sufsum[tott+flag]+num[i],flag=0;
}
else{
tott--;
sufsum[tott]=sufsum[tott+1]-num[i],flag=1;
}
}
tott=0;flag=1;
for(register ll i=1;i<=n;i++)
{
if(num[i]>0)
numm[tott+=flag]+=num[i],flag=0;
else
numm[++tott]=num[i],flag=1;
}
ll now;
maxx=presum[tot];
for(register ll i=1;i<=tot;i++)
{
if(numm[i]>0){
continue;
}
if(numm[i+1]>0)
{
now=max(presum[tot],presum[i]-numm[i+1]+sufsum[i+2]);
maxx=max(now,maxx);
}
else{
maxx=max(maxx,presum[i]+sufsum[i+1]);
}
}
printf("%lld\n",maxx);
}
return 0;
}
T3
这道题又是大佬口中的 一眼就能看出结论的题:
存在一条最短路,其x坐标单调递增是引用
存在一条最短路,满足引理1的性质,同时只在矩形的边界处拐弯
而且我们会发现最终的答案为 终点的横坐标+斯派克在纵轴上反复横跳的距离 然后我们只需要求出在纵轴上反复横跳的最短距离了
显然一个矩形 其有用的线段就只是 左侧的边 因为如果你走到了右侧的边内 相当于你由端点继续向前走 再向右侧的边的方向走 两者本质一样因此可以将右侧的边 无视。(好难写啊 相当于下面这一副图红色边 与 黑色边 本质相同)
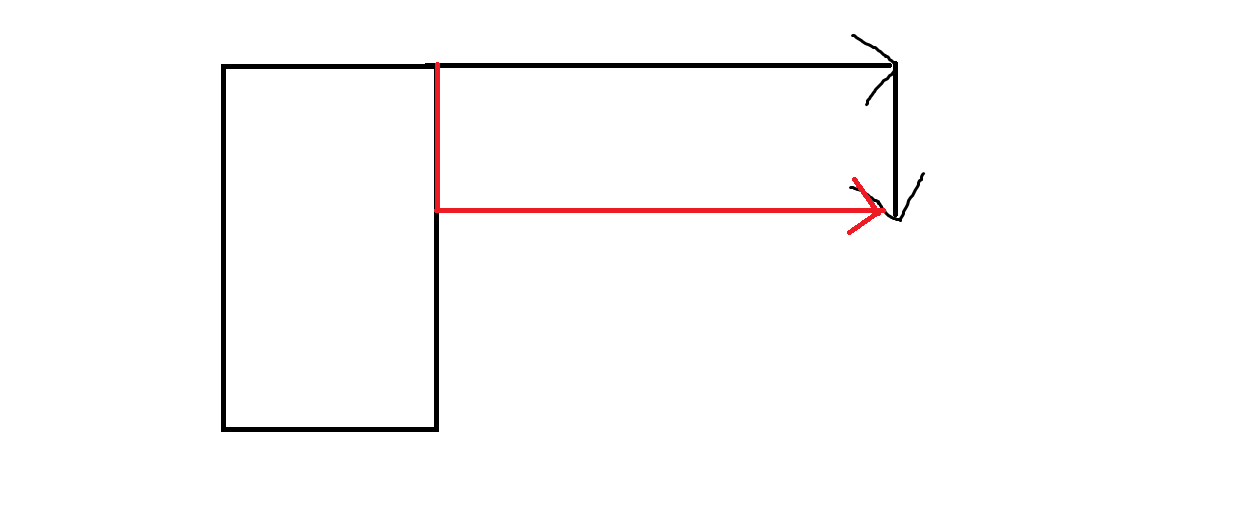
所以我们可以用扫描线的思想 用一条线(相当于斯派克)扫过去 求出我们要求的矩形的端点的前驱

然后求出了前驱之后用dp的方法 通过其前驱转移 到自己
细节: 需要在开头和结尾创建一个本不存在的线段 不然会炸!
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
const int maxn=500010;
struct node{
int x,low,high;
}line[maxn<<1];
struct nodee{
int l,r,tag,key;
#define l(x) tree[x].l
#define r(x) tree[x].r
#define tag(x) tree[x].tag
#define key(x) tree[x].key
}tree[maxn<<3];
int n,dest,cnt_l,lsh[maxn<<1],ls,cnt_lsh;
int pre[maxn][2],f[maxn][2];
inline bool line_cmp(node a,node b)
{
return (a.x<b.x || (a.x==b.x && a.low<b.low) || (a.x==b.x && a.low==b.low && a.high<b.high));
}
void build(int node,int l,int r)
{
l(node)=l;r(node)=r;
if(l==r){
return ;
}
int mid=(l+r)>>1;
build(node*2,l,mid);
build(node*2+1,mid+1,r);
}
inline void push_down(int node){
if(tag(node)){
tag(node<<1)=tag(node<<1|1)=tag(node);
key(node<<1)=key(node<<1|1)=tag(node);
tag(node)=0;
}
}
int query(int node,int ques)
{
if(l(node)==r(node) && l(node)==ques) return key(node);
push_down(node);
int mid=(l(node)+r(node))>>1;
if(ques<=mid) return query(node<<1,ques);
else return query(node*2+1,ques);
}
void modify(int node,int ql,int qr,int key)
{
if(ql>r(node) || l(node)>qr) return ;
if(ql<=l(node) && r(node)<=qr)
{
key(node)=tag(node)=key;
return ;
}
push_down(node);
modify(node<<1,ql,qr,key);modify(node<<1|1,ql,qr,key);
}
int min(int x,int y){
return (x<y)?x:y;
}
int abs(int x)
{
return (x<0)?-x:x;
}
int main()
{
n=read();dest=read();
line[++cnt_l]={0,0,0};line[++cnt_l]={dest,0,0};
for(register int i=1,a,b,c,d;i<=n;i++)
{
a=read();b=read();c=read();d=read();
if(b>d)
swap(b,d);
lsh[++cnt_lsh]=b;lsh[++cnt_lsh]=d;
line[++cnt_l]={a,b,d};//对于一个矩形 其所有用的线只有 左边的线
}
lsh[++cnt_lsh]=0;
sort(line+1,line+1+cnt_l,line_cmp);
sort(lsh+1,lsh+1+cnt_lsh);
ls=unique(lsh+1,lsh+1+cnt_lsh)-lsh-1;
for(register int i=1;i<=cnt_l;i++){
line[i].low=lower_bound(lsh+1,lsh+1+ls,line[i].low)-lsh;
line[i].high=lower_bound(lsh+1,lsh+1+ls,line[i].high)-lsh;
}
//这个是处理 如果有多个x ==0 的线 将 起点排在最前面
for(register int i=2;i<=cnt_l;i++)
{
if(line[i].x) break;
if(!lsh[line[i].low] && !lsh[line[i].high]){
swap(line[i],line[1]);break;
}
}
build(1,1,ls);
for(register int i=1;i<=cnt_l;i++)
{
pre[i][0]=query(1,line[i].low);
pre[i][1]=query(1,line[i].high);
modify(1,line[i].low,line[i].high,i);
}
for(register int i=2;i<=cnt_l;i++)
{
int prefix=max(1,pre[i][0]);//这里是处理 起点的特判
f[i][0]=min(f[prefix][0]+abs(lsh[line[i].low]-lsh[line[prefix].low]),f[prefix][1]+abs(lsh[line[i].low]-lsh[line[prefix].high]));
prefix=max(1,pre[i][1]);
f[i][1]=min(f[prefix][0]+abs(lsh[line[i].high]-lsh[line[prefix].low]),f[prefix][1]+abs(lsh[line[i].high]-lsh[line[prefix].high]));
}
printf("%d",f[cnt_l][0]+dest);
}



