2019-10-12

T1

T1是一道树上差分的题。首先看到题目要求环，我们就应该想到树是没有环的，但是！树加上一条边就有环了 所以我们在这道题中首先 dfs出一棵树 然后再将非树边一条一条的进行树上差分
关于树上差分 翻一翻别人的博客吧
这道题中 calc函数相当于把属于环中的点++，出现几次加几次的那种，至于为什么这样做是可行的 建议手动样例一下

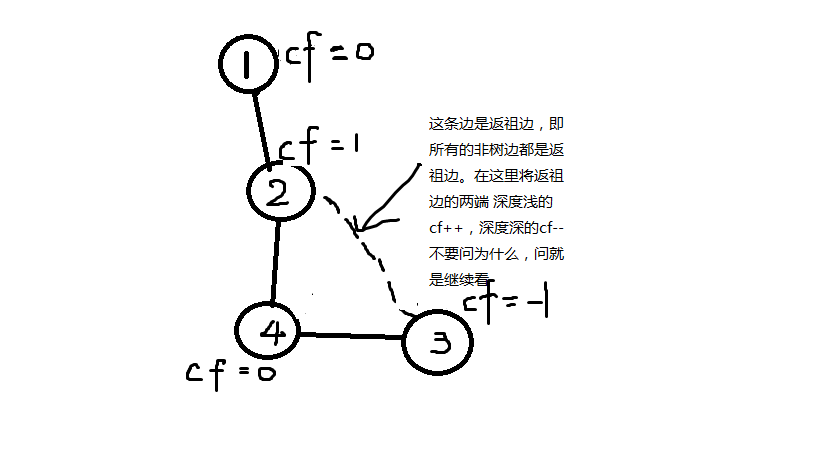
这是一开始的亚子

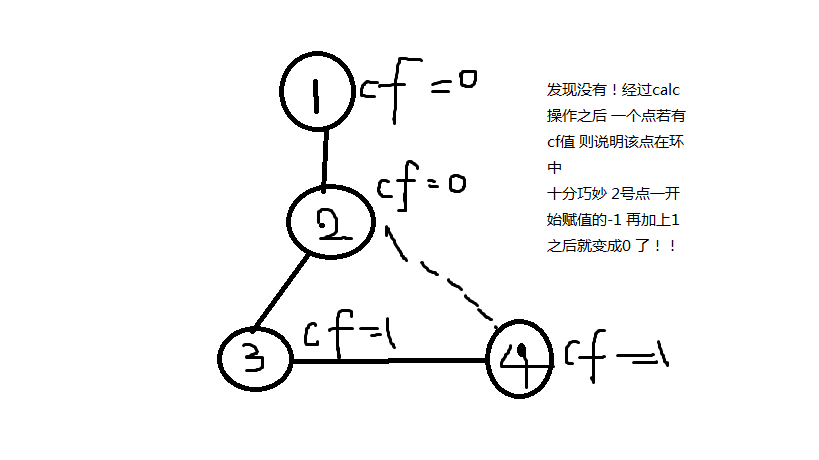
这是calc之后的亚子注意这里3,4号节点的编号写反了（失误但是没办法太笨了）

这是经过get了之后

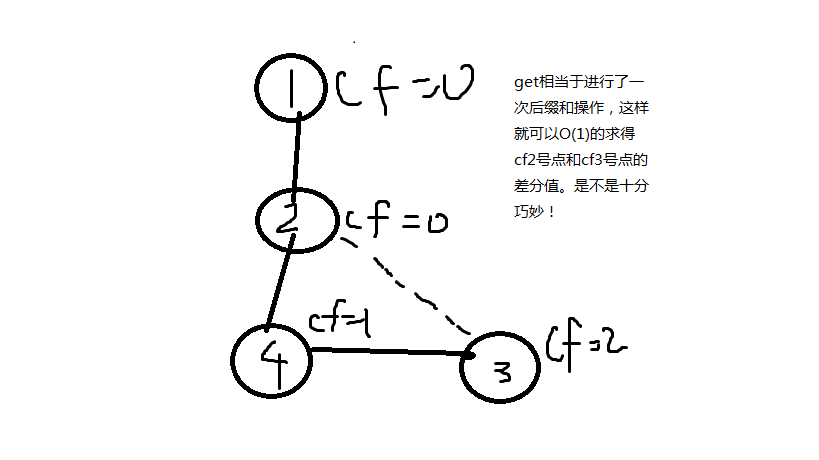
在经过了get之后可以用cf[3]-cf[2]于dep[3]-dep[2] 其中dep[3]-dep[2]相当于这两个点之间的距离 若cf[3]-cf[2] == dep[3] - dep[2] 说明了这是一个简单环 否则就说明这不是一个简单环

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;
const int maxn=1000050;
int first[maxn<<1],next[maxn<<1],to[maxn<<1];
struct node{
	int in,a,b,flag;
}e[maxn];
int n,m,dep[maxn],cf[maxn],x,y,visit[maxn],fa[maxn],id[maxn];
int tot=0;
int read()
{
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0' || ch>'9')
	{
		if(ch=='-')
			f=-1;
		ch=getchar();
	}
	while(ch>='0' && ch<='9')
	{
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}

void add(int x,int y)
{
	tot++;
	next[tot]=first[x];
	first[x]=tot;
	to[tot]=y;
}

void dfs(int x,int f)
{
	visit[x]=1;
	for(int i=first[x];i;i=next[i])
	{
		int y=to[i];
		if(visit[y] || f==y)
			continue;
		e[(i+1)>>1].in=1;
		dep[y]=dep[x]+1;
		fa[y]=x;
		id[y]=i;
		dfs(y,x);
	}
}	

void calc(int x,int f)
{
	visit[x]=1;
	for(int i=first[x];i;i=next[i])
	{
		int y=to[i];
		if(visit[y] || f==x )
			continue ;
		calc(y,x);cf[x]+=cf[y];
	}
}

void get(int x,int f)
{
	visit[x]=1;
	for(int i=first[x];i;i=next[i])
	{
		int y=to[i];
		if( visit[y] || f == x )
			continue ;
		cf[y]+=cf[x];get(y,x); 
	}
}

void get_sre(int v,int u)
{
	while(u^v) // 相当于u!=v 
	{
		e[(id[v]+1)>>1].flag = 1; 
		v=fa[v];
	}
}

int main()
{
	n=read();m=read();
	for(int i=1;i<=m;i++)
	{
		x=read();y=read();
		e[i].a=x;e[i].b=y;
		add(x,y);add(y,x);
	}
	for(int i=1;i<=n;i++) 
		if(!visit[i]) 
			dfs(i,0);
	for(int i=1;i<=m;i++)
	{
		if(e[i].in)	continue;
		x=e[i].a;y=e[i].b;
		if(dep[x]>dep[y])	swap(x,y);
		cf[x]--;cf[y]++;
	}
	memset(visit,0,sizeof(visit));
	for(int i=1;i<=n;i++)	if(!visit[i]) calc(i,0);
	memset(visit,0,sizeof(visit));
	for(int i=1;i<=n;i++)	if(!visit[i]) get(i,0);
	for(int i=1;i<=m;i++)
	{
		if(e[i].in)	continue;
		x=e[i].a;y=e[i].b;
		if(dep[x]>dep[y])	swap(x,y);
		if(dep[y]-dep[x]==cf[y]-cf[x]) get_sre(y,x),e[i].flag=1;
	}
	int ans=0;
	for(int i=1;i<=m;i++)
		if(e[i].flag)
			ans^=i;
	printf("%d",ans);
	return 0;
}

剩下的题我要先咕咕咕咕（不是先是永远）