最大流之二分图匹配
证明
Problem里面的任何一个解都能转化成G里面的一个可行流,G里面的任何一个可行流,都可以转换成Problem里面的一个可行方案,这样就可以证明这两个集合的方案是一一对应,等价的
所以可行解里面的最大值即为最大可行流
例题一 飞行员配对方案
https://www.luogu.com.cn/problem/P2756
本题的题意就是最大二分图匹配,然后考虑建边
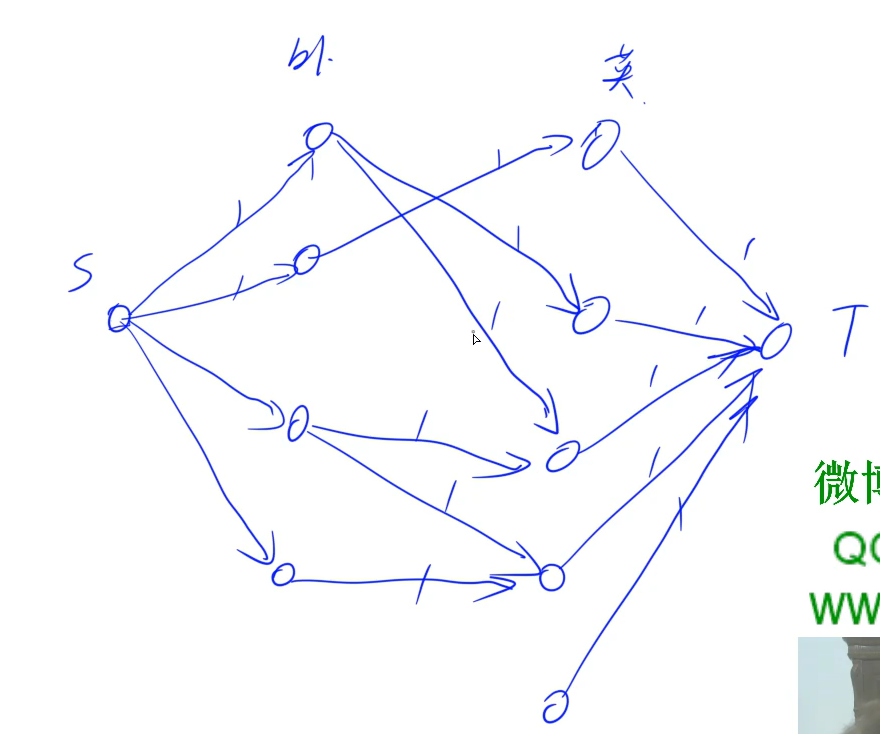
首先建立源点和汇点,然后因为每个飞行员只能用一次,所以源点向外籍飞行员建立一条容量为1的边,即表示只能在匹配中这个点出现一次,英国飞行员向汇点连一条容量为1的边,也表示每个英国飞行员只能使用一次
然后就是外籍飞行员与英籍飞行员之间的匹配了,直接连边即可
流量守恒并且满足容量限制,所以正确
#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=10010,M=200010,INF=1e15;//根据边的大小,来调整N,M,INF
int n,m,S,T;
int h[N],e[M],f[M],ne[M],idx;
int q[N],d[N],cur[N];
void add(int a,int b,int c){
e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;
e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;
}
bool bfs(){//规划分层图,然后判断是否存在增广路
int hh=0,tt=0;
memset(d,-1,sizeof d);
q[0]=S,d[S]=0,cur[S]=h[S];//起点的层数为0
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1&&f[i]){//只有这条边有流量的时候,才能继续走下去
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T)return true;//如果能搜到T的话,那么就说明可以找到一条增广路
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i&&flow<limit;i=ne[i]){//当前弧优化
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1&&f[i]){
int t=find(ver,min(f[i],limit-flow));
if(!t) d[ver]=-1;
f[i]-=t,f[i^1]+=t,flow+=t;
}
}
return flow;
}
int dinic(){
int ans=0,flow;
while(bfs()) while(flow=find(S,INF)) ans+=flow;
return ans;
}
void slove(){
cin>>m>>n;
S=0,T=n+1;
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++) add(S,i,1);
for(int i=m+1;i<=n;i++) add(i,T,1);
int a,b;
while(cin>>a>>b){
if(a==-1) break;
add(a,b,1);
}
cout<<dinic()<<endl;
for(int i=0;i<idx;i+=2){
if(e[i]>m&&e[i]<=n&&!f[i]){
cout<<e[i^1]<<" "<<e[i]<<endl;//i的反向边编号是i^1,跟EK算法的那个原理一致
}
}
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
while(T--) slove();
}
例题二,圆桌骑士
https://www.luogu.com.cn/problem/P3254
思路就是:源点对每个单位连一条有向边,容量就是这个单位派出的代表人数,然后每个餐桌都对汇点连一条边,每条边的容量就是这个餐桌可以容纳的人的数量
然后就是每个单位对所有的餐桌都连一条边,并且容量为1(因为题目要求每个餐桌不允许有相同的代表)
然后这题就完美结束了
#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=10010,M=200010,INF=1e15;//根据边的大小,来调整N,M,INF
int n,m,S,T;
int h[N],e[M],f[M],ne[M],idx;
int q[N],d[N],cur[N];
void add(int a,int b,int c){
e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;
e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;
}
bool bfs(){//规划分层图,然后判断是否存在增广路
int hh=0,tt=0;
memset(d,-1,sizeof d);
q[0]=S,d[S]=0,cur[S]=h[S];//起点的层数为0
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1&&f[i]){//只有这条边有流量的时候,才能继续走下去
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T)return true;//如果能搜到T的话,那么就说明可以找到一条增广路
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i&&flow<limit;i=ne[i]){//当前弧优化
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1&&f[i]){
int t=find(ver,min(f[i],limit-flow));
if(!t) d[ver]=-1;
f[i]-=t,f[i^1]+=t,flow+=t;
}
}
return flow;
}
int dinic(){
int ans=0,flow;
while(bfs()) while(flow=find(S,INF)) ans+=flow;
return ans;
}
int rr[N],cc[N];
vector<int> ans[N];
void slove(){
memset(h,-1,sizeof h);
cin>>m>>n;//m表示单位数,n表示桌子的数量
int sum=0;
for(int i=1;i<=m;i++){
cin>>rr[i];
sum+=rr[i];
}
for(int i=1;i<=n;i++) cin>>cc[i];
S=0,T=n+m+1;
for(int i=1;i<=m;i++) add(S,i,rr[i]);
for(int i=1;i<=n;i++) add(i+m,T,cc[i]);
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
add(i,j+m,1);
if(dinic()==sum){
cout<<1<<endl;
for(int i=0;i<idx;i++){
if(e[i]>m&&e[i]<=n+m&&!f[i]){
ans[e[i^1]].push_back(e[i]);
}
}
for(int i=1;i<=m;i++){
sort(ans[i].begin(),ans[i].end());
for(auto zz:ans[i]) cout<<zz-m<<" ";
cout<<endl;
}
}else cout<<0<<endl;
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
while(T--) slove();
}
