最大网络流基本概念--EK,dinic
1. 基本概念
1.1 流网络，不考虑反向边
如果存在反向边也没事,不如有u->v和v->u两条边,那么就可以新加入一个点 p,u->v,v->p,p->u,转化为这三条边
1.2 可行流，不考虑反向边
1.2.1 两个条件：容量限制、流量守恒
容量限制:每条边流的不能超过这条边的权值
流量守恒:每个点流入的流量等于流出去的流量()
1.2.2 可行流的流量指从源点流出的流量 - 流入源点的流量
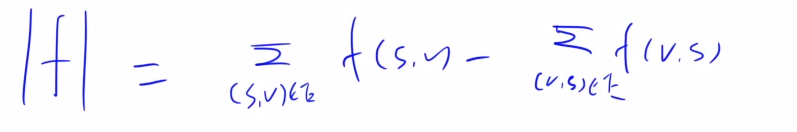
1.2.3 最大流是指最大可行流
1.2.4 一个可行流的实例图:(红色表示这条边上的实际流,蓝色表示这条边的容量)
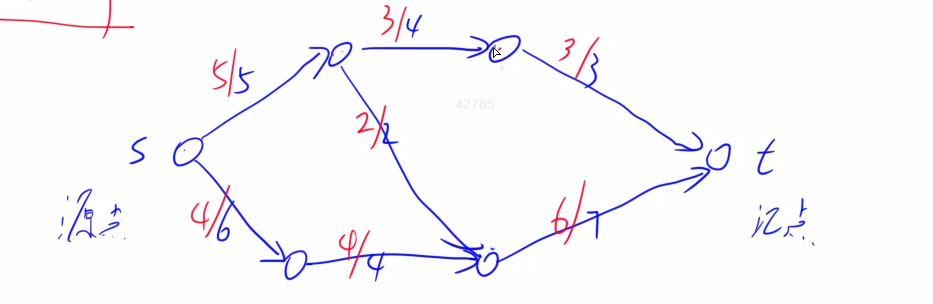
1.3 残留网络，考虑反向边，残留网络的可行流f' + 原图的可行流f = 原题的另一个可行流
(1) |f' + f| = |f'| + |f|
(2) |f'| 可能是负数
残留网络实例,下图为上图的残留网络,原图为f,残留网络记为G[f]
正向边为容量-原图流量,反向边为原图流量
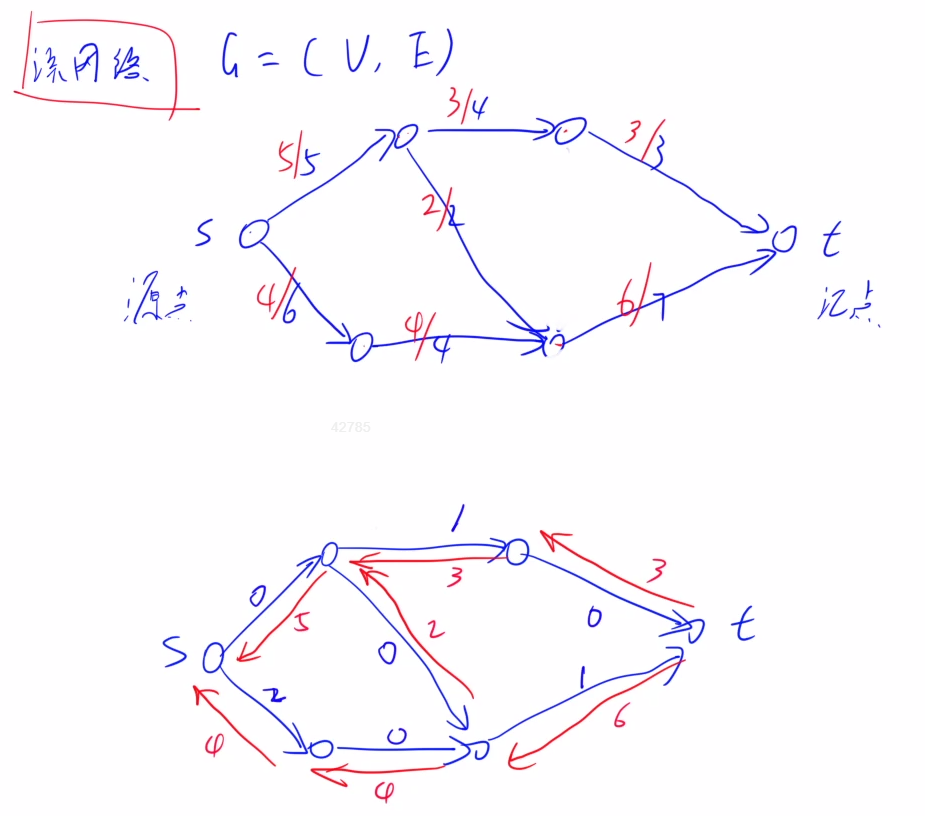
1.4 增广路径
在残留网络从,从源点开始沿着大于0的边走,如果能到达终点,那么就是一条增光路径,如下图所示的红色路径
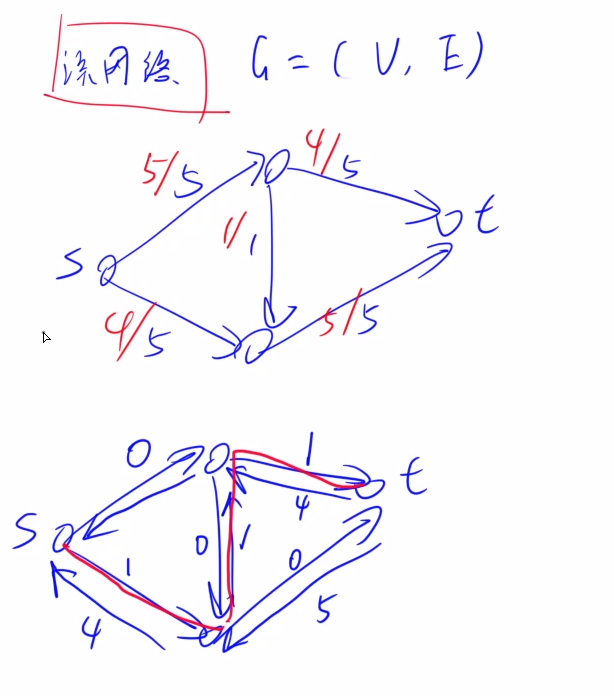
重要: 如果一个可行流的残留网络没有增广路径,那么这个可行流就是一个最大流
1.5 割
1.5.1 割的定义
一个图G=(V,E),然后把点划分成两个集合S和T,并且保证这两个集合是不重不漏的,并且源点s∈S,汇点t∈T
1.5.2 割的容量，不考虑反向边，“最小割”是指容量最小的割。
所有S连向T的边的容量的和,称为割的容量,记为c(S,T)
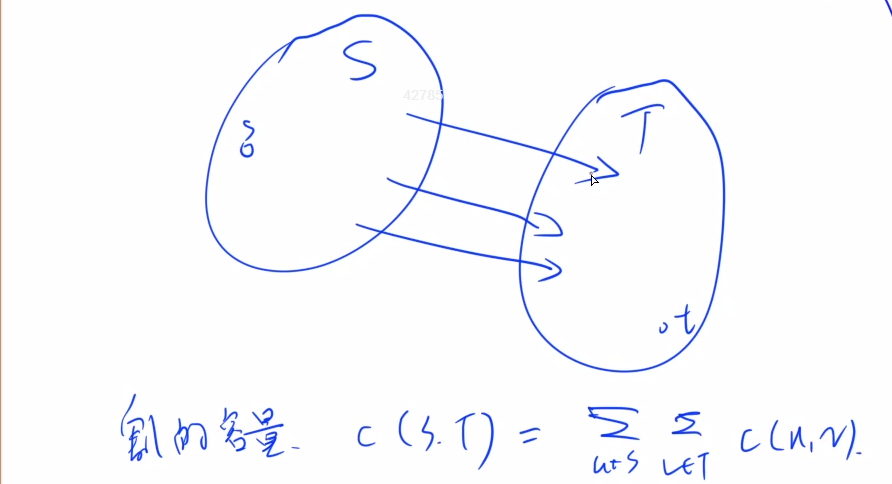
1.5.3 割的流量，考虑反向边，f(S, T) <= c(S, T)
割的流量=S流到T的流量-T流到S的容量
1.5.4 对于任意可行流f，任意割[S, T]，|f| = f(S, T),即割的流量等于可行流的流量
1.5.5 对于任意可行流f，任意割[S, T]，|f| <= c(S, T)
1.5.6 最大流最小割定理,以下三个条件都是等价的
(1) 可行流f是最大流
(2) 可行流f的残留网络中不存在增广路
(3) 存在某个割[S, T]，|f| = c(S, T)
1.6. 算法
1.6.1 EK O(nm^2) -- 最大流所有算法中最简单的实现,经验是可以处理点数+边数处于[1000,10000]的网络范围
原理就是不断维护残留网络,即不断的寻找增广路径,然后把这条增广路径给并到可行流内,不断重复这个过程,直到不存在残留网络
#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=1010,M=20010,INF=1e15;
int n,m,S,T;
int h[N],e[M],f[M],ne[M],idx;//f数组表示容量
int q[N],d[N],pre[N];
//q表示宽搜的队友,d[i]表示从起点走到i,当前所有边的容量最小值,pre[i]用来记录路径
bool st[N];
/*
这边正向边的编号与反向边的编号做了一个巧妙的变换
比如正向边编号为t,反向边编号为s
那么t^1=s;
0 1 0是正向边,1是反向边
2 3
4 5
依此类推赋值边的编号
*/
void add(int a,int b,int c){
e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;//正向边
e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;//反向边,一开始残留网络的反向边的权值为0
}
bool bfs(){
int hh=0,tt=0;
memset(st,false,sizeof st);
q[0]=S,st[S]=true,d[S]=INF;
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(!st[ver]&&f[i]){//如果当前的点没被遍历过,并且连向的边不为0的话
st[ver]=true;
d[ver]=min(d[t],f[i]);
pre[ver]=i;//记录前驱边的编号,然后就可以获得完整的路径信息,方便对残留网络进行更新
if(ver==T)return true;
q[++tt]=ver;
}
}
}
return false;
}
int EK(){
int ans=0;//答案
while(bfs()){
ans+=d[T];
for(int i=T;i!=S;i=e[pre[i]^1]){
f[pre[i]]-=d[T],f[pre[i]^1]+=d[T];
//pre[i]的反向边编号是pre[i]^1,所以e[pre[i]^1]的点就是该点在记录路径上的上一个点
}
}
return ans;
}
void slove(){
cin>>n>>m>>S>>T;
memset(h,-1,sizeof h);
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
cout<<EK()<<endl;
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
while(T--) slove();
}
1.6.2 Dinic O(n^2m) -- 经验是可以处理点数+边数处于[10000,100000]的网络范围
一个图可能不止一条增广路,dinic的思想就是用dfs爆搜出多条增广路,一次增广多条路径,大大提高增广的效率
然后为了防止出现环而影响判断,引入一个分层图的概念,每个点的层数是到起点的最短距离,然后路径设置是只能从层数低跳到层数高的点,这样就能抑制环的出现,提高效率
然后就是把所有这个分层图能搜索到的增广路径,全部统一增广一遍
步骤:
1.bfs一遍-->建立分层图
2.dfs 找出所有能够增广的路径
#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=10010,M=200010,INF=1e15;//根据边的大小,来调整N,M,INF
int n,m,S,T;
int h[N],e[M],f[M],ne[M],idx;//f数组表示容量
int q[N],d[N],cur[N];
//q表示宽搜的队列,d[i]表示i这个点的层数,cur是当前弧优化
/*
当前弧优化的意思:
每次遍历一个点的邻点的时候,都会按照固定的顺序去遍历每条边
然后dfs的过程就是去枚举每条路径,然后把这条路径的容量减去当前路径流量的最小值
然后每次dfs完之后,每条边的流量都会加上一个值,而一旦这条边的容量满了,那么就没有
继续遍历这条边的必要,所以后面遍历的时候,就可以直接跳过这条边
所以一开始每个点的cur[i]=h[i],当f[h[i]]这条边满的时候,也就没继续遍历的必要,cur[i]=ne[h[i]]
*/
void add(int a,int b,int c){
e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;//正向边
e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;//反向边,一开始残留网络的反向边的权值为0
}
bool bfs(){//规划分层图,然后判断是否存在增广路
int hh=0,tt=0;
memset(d,-1,sizeof d);
q[0]=S,d[S]=0,cur[S]=h[S];//起点的层数为0
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1&&f[i]){//只有这条边有流量的时候,才能继续走下去
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T)return true;//如果能搜到T的话,那么就说明可以找到一条增广路
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){//limit表示从源点走到u这个点,能流的最大的流量
if(u==T) return limit;
int flow=0;//flow表示从u这个点开始,往后流的最多的流量是多少
//flow一定是要小于等于limit的,这个毋庸置疑的,当flow=limit的时候,说明u这个点往外已经把流量全部流完了
for(int i=cur[u];~i&&flow<limit;i=ne[i]){//当前弧优化
cur[u]=i;//i前面的边都流完了
int ver=e[i];
if(d[ver]==d[u]+1&&f[i]){
int t=find(ver,min(f[i],limit-flow));
if(!t) d[ver]=-1;//这个点出发到终点是没有流量大于0的路径的,那么就可以删掉了
f[i]-=t,f[i^1]+=t,flow+=t;
}
}
return flow;
}
int dinic(){
int ans=0,flow;
while(bfs()) while(flow=find(S,INF)) ans+=flow;
return ans;
}
void slove(){
cin>>n>>m>>S>>T;
memset(h,-1,sizeof h);
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
cout<<dinic()<<endl;
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
while(T--) slove();
}
