差分约束系统

一.差分约束

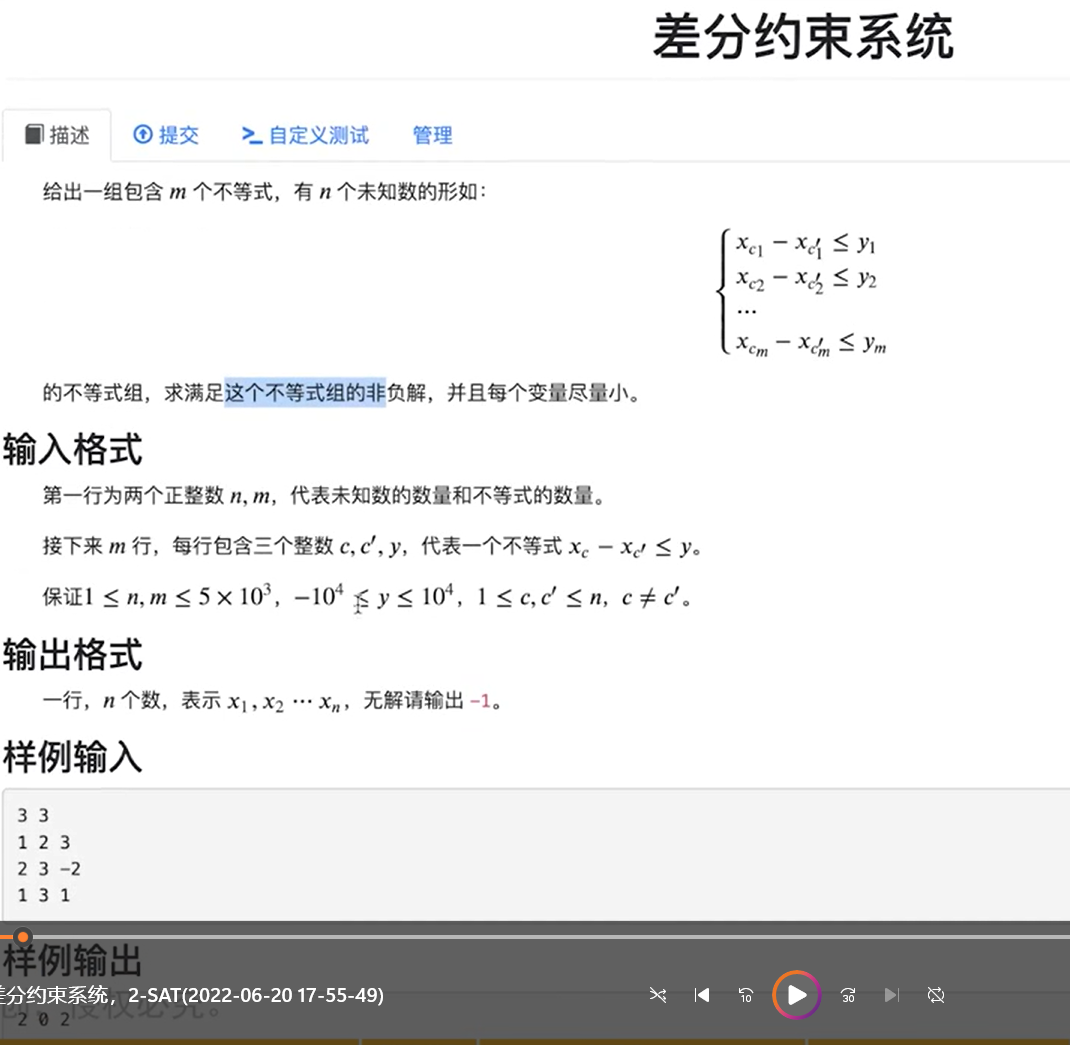
问题是给定x1,x2,……,xn,然后给定出若干限制
xi-xj<=c,然后求解/无解
xi-xj>=c可以转换成xj-xi<=-c;
xi-xj=c,可以转换为xi-xj<=c,xi-xj>=c;

最暴力的想法就是一开始给所有的变量都赋值为0,然后每次都暴力循环所有的限制,如果有限制不满足,直接改变一个限制的值
其实这个想法就相当于是bellman-ford算法,时间复杂度是o(nm)的
然后我们再解决其中的一个问题,就是非负解,我们可以引入一个变量x0
然后xi-x0>=0,相当于x0-xi<=0
这样做之后,得到一组解,然后就可以将每个解都减去x0,这样x0就变成0,而其他等式依然满足条件,即xi-x0>=0均满足条件,所以可以得到非负整数解

注意:xu-xv<=w,相当于u连向v的边,权值为W

然后上结论:
最短路对应的是最大值,然后最小值就是给xi变成-xi,xi-xj<=w --> (-xi)-(-xj)<=w --> xj-xi<=w,即j连向i,并且边权为w的最短路,因为xi取到最大值,那么-xi一定是相当于取到最小值的

所以最短路就是求最大值,将边的方向反过来后的最短路就是最小值(求解的时候也要反回来,将xi-x0改为x0-xi)
或者是这样求解最小值
xu-xv<=w,改为xv>=xu-w,然后跑最长路,xv=max(xu-w,xv);

https://www.luogu.com.cn/record/194743808

求最大值,最短路

#include<bits/stdc++.h>

#define x first
#define y second
#define endl '\n'
#define int long long
 
using namespace std;
 
const int N=1e6+10,INF=1e16,mod=1e9+7,M=2e5+10;

typedef pair<int,int> PII;

vector<array<int,3>>E;
int x[N];

void slove(){
	int n,m;
	cin>>n>>m;
	for(int i=0;i<m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		E.push_back({u,v,w});
	}
	
	for(int i=1;i<=n;i++){
		E.push_back({0,i,0});//x0-xi<=0,即xi-x0>=0 
	}
	
	for(int i=1;i<=n;i++) x[i]=1<<30;//bellman-ford算法,所有点一开始均为最大值
	
	for(int i=0;i<=n;i++){
		for(auto [u,v,w]:E){
			x[u]=min(x[u],x[v]+w);//x[u]<=x[v]+w的限制
		}
	}
	
	
	for(auto [u,v,w]:E){
		if(x[u]>x[v]+w){//有负环的情况
			cout<<"NO"<<endl;
			return ;
		}
	}
	
	for(int i=1;i<=n;i++) cout<<x[i]-x[0]<<" ";
}

signed main(){
	ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
	int T=1;
//	cin>>T;
	while(T--) slove();
}

求最小值,最短路写法

#include<bits/stdc++.h>

#define x first
#define y second
#define endl '\n'
#define int long long
 
using namespace std;
 
const int N=1e6+10,INF=1e16,mod=1e9+7,M=2e5+10;

typedef pair<int,int> PII;

vector<array<int,3>>E;
int x[N];

void slove(){
	int n,m;
	cin>>n>>m;
	for(int i=0;i<m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		E.push_back({v,u,w});//建反边
	}
	
	for(int i=1;i<=n;i++){
		E.push_back({i,0,0});//x0-xi<=0,即xi-x0>=0,建反边
	}
	
	for(int i=1;i<=n;i++) x[i]=1<<30;//bellman-ford算法,所有点一开始均为最大值
	
	for(int i=0;i<=n;i++){
		for(auto [u,v,w]:E){
			x[u]=min(x[u],x[v]+w);//x[u]<=x[v]+w的限制
		}
	}
	
	
	for(auto [u,v,w]:E){
		if(x[u]>x[v]+w){//有负环的情况
			cout<<"NO"<<endl;
			return ;
		}
	}
	
	for(int i=1;i<=n;i++) cout<<x[0]-x[i]<<" ";//反过来
}

signed main(){
	ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
	int T=1;
//	cin>>T;
	while(T--) slove();
}

求最小值,最长路写法

#include<bits/stdc++.h>

#define x first
#define y second
#define endl '\n'
#define int long long
 
using namespace std;
 
const int N=1e6+10,INF=1e16,mod=1e9+7,M=2e5+10;

typedef pair<int,int> PII;

vector<array<int,3>>E;
int x[N];

void slove(){
	int n,m;
	cin>>n>>m;
	for(int i=0;i<m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		E.push_back({u,v,w});
	}
	
	for(int i=1;i<=n;i++){
		E.push_back({0,i,0});
	}
	
	for(int i=1;i<=n;i++) x[i]=-(1<<30);//bellman-ford算法,最长路取max是负无穷大,最短路取min是正无穷大
	
	/*
	x[v]>=x[u]-w,即x[v]=max(x[v],x[u]-w);
	*/
	for(int i=0;i<=n;i++){
		for(auto [u,v,w]:E){
			x[v]=max(x[v],x[u]-w);//x[u]<=x[v]+w的限制
		}
	}
	
	
	for(auto [u,v,w]:E){
		if(x[u]>x[v]+w){//有负环的情况
			cout<<"NO"<<endl;
			return ;
		}
	}
	
	for(int i=1;i<=n;i++) cout<<x[i]-x[0]<<" ";//反过来
}

signed main(){
	ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
	int T=1;
//	cin>>T;
	while(T--) slove();
}

可以解决区间和问题,比如说[l,r]内的值的和大于等于x,还有a[l]>=x等都可以转化为前缀形式,然后差分约束求解