割点割边双连通分量
一.双连通分量,割点,割边
割点定义:对于一个连通图,如果删去这个点后,会存在两个及两个以上的连通图
割边定义:把一条边删掉后,这个图会被分割成两个部分,又称桥
双连通概念:分为点双连通分量和边双连通分量
点双连通:没有割点
边双连通:没有割边
双连通的性质:
对于点:对于任意两点u,v,都存在两条简单路径(简单路径不经过重复点),这两条简单路径点不相交(两条路径上的点都互不相同)
对于边:对于任意两点u,v,都存在两条简单路径,这两条简单路径边不相交
不难看出,一个图如果是点双,那么这个图也一定是边双
双连通分量:
抽象的定义:极大的点集,满足导出子图是点(或边)是双连通的
点双实例:(一个点可能在多个连通分量内)
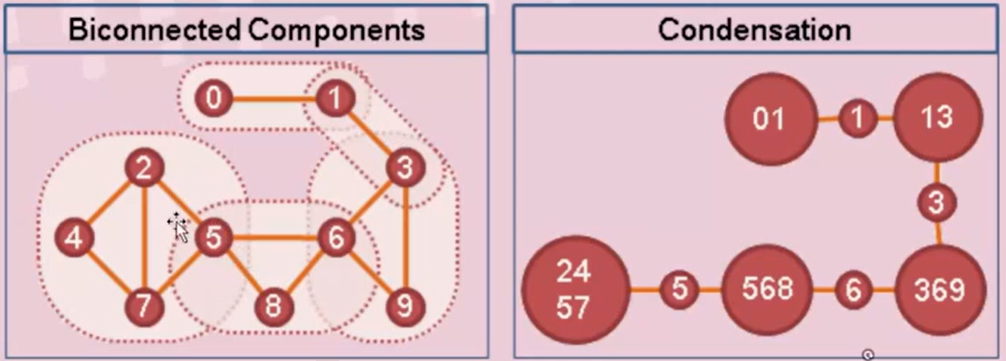
边双实例:
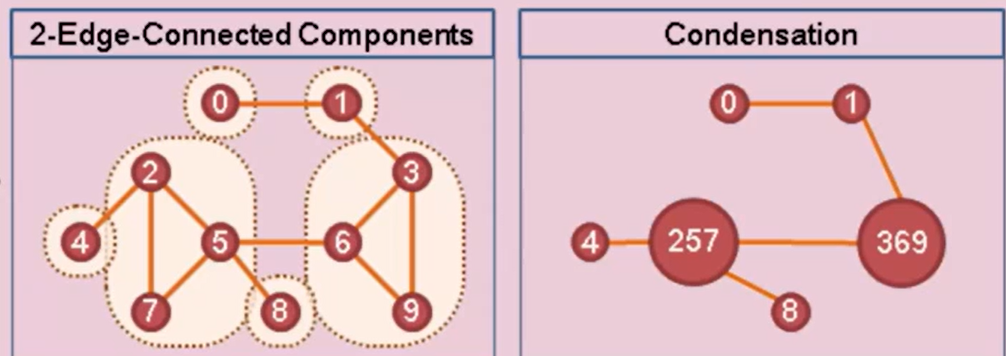
双连通分量缩图
边双:树
点双:圆方树(block tree)
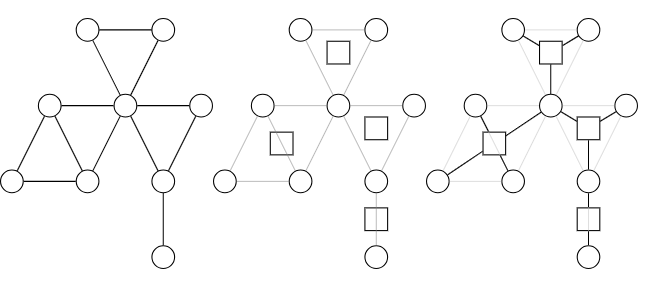
二.tarjan算法求双连通分量
1.割边(无向图)
DFS的话?只有返祖边和树边,假设有横叉边,那么横叉边一定是指向前面被遍历过的,而被遍历过的点,一个会遍历到这个横叉边,所以就矛盾了,故而不存在横叉边
首先返祖边一定不是割边,因为返祖边会形成一个环,删去后,图仍然连通
然后考虑树边,如果这条树边是割边的话,那么以这个点为根的子树就没有边返祖上去
所以用tarjan就行了(dfn,low)
例题:https://www.luogu.com.cn/problem/P1656
需要注意的是重边!
#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=1e6+10;
typedef pair<int,int> PII;
vector<int> e[N];
int dfn[N],low[N],idx,n,m;
vector<PII> bridge;
void dfs(int u,int fa){
dfn[u]=low[u]=++idx;
bool ok=false;//特判连向父亲节点的重边
for(auto v:e[u]){
if(!dfn[v]){
dfs(v,u);
}
if(v!=fa||ok) low[u]=min(low[u],low[v]);
if(v==fa) ok=true;
}
if(dfn[u]==low[u]&&fa!=-1){//找到了一个桥
bridge.push_back({min(u,fa),max(u,fa)});
}
}
void slove(){
int n,m;cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}
dfs(1,-1);
sort(bridge.begin(),bridge.end());
for(auto zz:bridge) cout<<zz.x<<" "<<zz.y<<endl;
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
// cin>>T;
while(T--) slove();
}
2.割点(无向图)
一个点u,若存在子树的返祖边最高就是u,那么u这个点就是割点
注意特殊情况:如果是根,并且只有一个儿子节点,那么他一定不是割点
#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=1e6+10;
typedef pair<int,int> PII;
vector<int> e[N];
int dfn[N],low[N],idx,n,m,cnt[N];
int sz,root;
//id表示u的父亲->u的这条边的编号
void dfs(int u,int fa){
dfn[u]=low[u]=++idx;
int ch=0;//儿子的个数
for(auto v:e[u]){
if(!dfn[v]){
dfs(v,u);
ch++;
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]) cnt[u]=1;//v跳不出去了
}else if(v!=fa){//返祖边,割点的话跟割边是不一样的,只能跳一次,并且不用判断与父亲节点的重边,因为这个点删掉之后,与父亲节点所连的边全部被删
low[u]=min(low[u],dfn[v]);
}
}
if(u==root&&ch==1) cnt[u]=0;
sz+=cnt[u];
}
void slove(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}
for(int i=1;i<=n;i++) if(!dfn[i]) root=i,dfs(i,-1);
cout<<sz<<endl;
for(int i=1;i<=n;i++)if(cnt[i]){
cout<<i<<" ";
}
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
// cin>>T;
while(T--) slove();
}
割边例题
思路:边双连通分量缩图就是一棵树,只需要考虑在这棵树上如何加边即可,而每次加边,就相当于把一个路径上的割边全部弄成非割边
首先树上的边,一定都是割边,然后要考虑的就是,加完边后,如果该树边被纳入到一个环内,那么就不是割边了
通过观察可以发现的就是,这题答案就是(叶子个数+1)/2;
题外话:有一个经典的构造,假设有m个叶子节点,那么要选至少多少条路径才能覆盖整颗树的节点?
按照DFS序给每个叶子节点赋个编号,然后就是i->i+m/2这样的形式选路径即可,最终需要的路径路径数量就是(m+1)/2;
#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=1e6+10;
typedef pair<int,int> PII;
vector<int> e[N];
int dfn[N],low[N],ins[N],bel[N],idx,n,m,cnt;
vector<int> cc[N];
stack<int> stk;
void dfs(int u,int fa){
dfn[u]=low[u]=++idx;
ins[u]=true;
stk.push(u);
bool ok=false;
for(auto v:e[u]){
if(!dfn[v]){
dfs(v,u);
}
if(v!=fa||ok) low[u]=min(low[u],low[v]);
if(v==fa) ok=true;
}
if(dfn[u]==low[u]){//找到了一个桥,那么栈里面的点,直到u,都是属于同一个边双连通分量,类似于强连通分量的缩点处理
++cnt;
while(true){
int v=stk.top();
cc[cnt].push_back(v);//边双分量
ins[v]=false;
bel[v]=cnt;
stk.pop();
if(v==u) break;
}
}
}
void slove(){
int n,m;cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}
dfs(1,-1);
int nleaf=0;
for(int i=1;i<=cnt;i++){
int cnte=0;
for(auto u:cc[i]){
for(auto v:e[u])if(bel[u]!=bel[v]) cnte++;//割边
}
if(cnte==1) nleaf++;//叶子节点连向的割边只有一条
}
// cout<<nleaf<<endl;
cout<<(nleaf+1)/2<<endl;
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
// cin>>T;
while(T--) slove();
}
例题2
https://www.luogu.com.cn/problem/P3469
#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=1e6+10;
typedef pair<int,int> PII;
vector<int> e[N];
int dfn[N],low[N],idx,n,m,sz[N],ans[N];
//id表示u的父亲->u的这条边的编号
void dfs(int u,int fa){
dfn[u]=low[u]=++idx;
sz[u]=1;
ans[u]=n-1;//被删除掉的点u,跟其他点都一定不连通
int cut=n-1;//剩余的连通的点的数量
for(auto v:e[u]){
if(!dfn[v]){
dfs(v,u);
sz[u]+=sz[v];
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){
ans[u]+=sz[v]*(n-sz[v]);//把u删掉后,以v为根的这颗子树与其他的节点一定不连通
cut-=sz[v];
}
}else if(v!=fa){
low[u]=min(low[u],dfn[v]);
}
}
ans[u]+=cut*(n-cut);//上面的连通部分
}
void slove(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}
dfs(1,-1);
for(int i=1;i<=n;i++)cout<<ans[i]<<endl;
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
// cin>>T;
while(T--) slove();
}
例题三（求出每个具体的点双连通分量板子）
https://www.luogu.com.cn/problem/P3225
1.首先考虑没有割点的情况
至少设置两个救援出口,因为会出现一个救援出口坍塌的情况,方案数为c[n][2]
2.有割点的情况
首先必须在叶子节点设立一个救援出口,因为若叶子节点连向的割点塌了的话,那么这个叶子节点就无路可走了
所以对于每个点连通分量而言,选择一个叶子节点即可
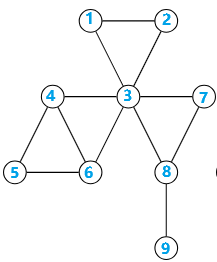
对于这张图来说:
点双集合为
1 3 2
3 4 5 6
3 8 7
8 9
#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=1e6+10;
typedef pair<int,int> PII;
vector<int> e[N];
int dfn[N],low[N],idx,n,m,cnt,cut[N];
stack<int> stk;
vector<int> cc[N];
/*
相当于求出每个点双连通分量的板子了
*/
void dfs(int u,int fa){
dfn[u]=low[u]=++idx;
stk.push(u);
int ch=0;
for(auto v:e[u]){
if(!dfn[v]){
dfs(v,u);
ch++;
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){//以u为根节点,并且u是割点,并且子树是以v为根节点的点双连通分量,然后求出一个点双连通分量(每个点双连通分量都有一个割点)
cut[u]=1;
++cnt;
cc[cnt].push_back(u);
while(true){
int w=stk.top();
cc[cnt].push_back(w);
stk.pop();
if(w==v) break;
}
}
}else if(v!=fa){
low[u]=min(low[u],dfn[v]);
}
}
if(u==1&&ch<=1) cut[u]=0;
}
void slove(int u,int ca){
m=u;
for(int i=1;i<=1000;i++) e[i].clear();
int n=0;
for(int i=0;i<m;i++){
int u,v;cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
n=max(n,max(u,v));
}
for(int i=1;i<=n;i++){
dfn[i]=low[i]=cut[i]=0;
idx=cnt=0;
cc[i].clear();
}
while(!stk.empty())stk.pop();
for(int i=1;i<=n;i++)if(!dfn[i])dfs(i,0);
cout<<"Case "<<ca<<": ";
if(cnt==1){//只有一个点双,说明所有点都是双连通的
int n=cc[1].size();
cout<<2<<" "<<n*(n-1)/2<<endl;
}else {
int ans1=0,ans2=1;
for(int i=1;i<=cnt;i++){
int ncut=0;
for(auto u:cc[i]) ncut+=cut[u];//找割点,一个边双连通分量最多只有一个割点
if(ncut==1){
ans1+=1;
ans2*=(int)cc[i].size()-1;
}
}
cout<<ans1<<" "<<ans2<<endl;
}
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
cin>>T;
int p=1;
while(T!=0){
slove(T,p++);
cin>>T;
}
}
