bitset

1.位运算的常见函数
__builtin_popcount(x) //x二进制内1的个数(unsigned int)
__builtin_popcountll(x) //longlong版本
__builtin_parity(x) //二进制下的1的个数的奇偶性
__builtin_parityll(x) //long long版本
__builtin_ctz(x)//x二进制末尾0的个数
__builtin_clz(x)//x二进制开头0的个数
log2(x)=31-__builtin_clz(x);
以上函数的时间复杂度均为o(1)
2.bitset中常见的东西
bitset<1000>a;//长度为1000的bool数组
访问的话必须强转为int类型
比如(int)a[0],(int)a.any(),(int)a.count;
a.any();//判断存不存在至少一个1
a.none();//是不是全都是0
a.count();//统计这里面有几个1
a.set();//把所有数位都变成1
a.set(x);//把第x位变成1
a.reset(x);//把第x位变成0
a.reset();//把所有位变成0
找到第一个1的位置,和下一个1的位置

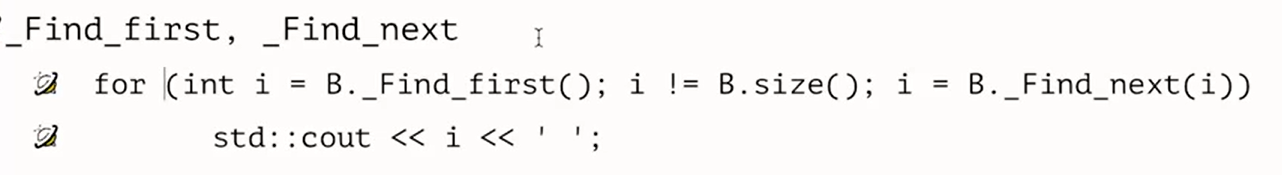
1.简单题

/*
正常思路:
dp[i][j]:表示前i个数,和为j的方案.
因为对于异或来说,一个数出现奇数次,那就相当于出现一次,出现偶数次就相当于没出现过
所以dp[i][j]:表示前i个数,和为j的方案数的奇偶性
复杂度是:
n*sum(a[i])=1000*2e6=2e9
考虑bitset优化?
首先考虑转移上怎么转换 
f[i][j]=(f[i-1][j-a[i]]+f[i-1][j])%2
相当于
f[i][j]=(f[i-1][j-a[i]]^f[i-1][j])
直接bitset即可
复杂度相当于是2e9/64 
*/

bitset<2000001>f;

void slove(){
	int n;cin>>n;
	f[0]=1;
	for(int i=0;i<n;i++){
		int x;cin>>x;
		f=f^(f<<x);
	}
	int ans=0;
	for(int i=0;i<=2000000;i++){
		if(f[i]) ans^=i;
	}
	cout<<ans<<endl;
} 

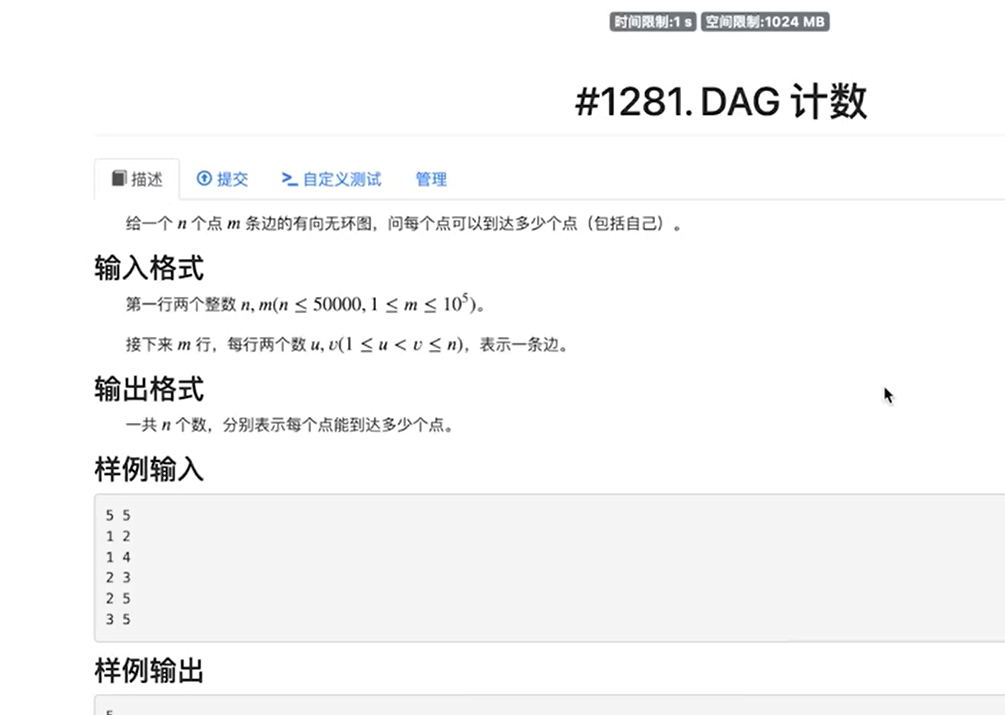
2.DAG计数

const int N=50010;

bitset<N>f[N];
vector<int>e[N];

void slove(){
	int n,m;cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v;cin>>u>>v;
		e[u].push_back(v);
	}
	for(int u=n;u>=1;u--){
		f[u][u]=1;
		for(auto v:e[u]) f[u]|=f[v];
	}
	
	for(int i=1;i<=n;i++) {
		cout<<f[i].count()<<endl;
	}
}