【高中数学】导数压轴题——极值点偏移
极值点偏移——从入门到入土
极值点偏移,也可以说是零点偏移,反正怎么叫都行,具体是指一种某一单峰(可以为多峰,只是单峰的变种)函数关于\(x=a\)总体上对称,但函数的极值点并不是两零点的中点(即\(\frac{x_1+x_2}{2}\)) ,而是处于一种偏移状态,其中为\(x_1+x_2>2a或x_1+x_2<2a\)的这么一种状态,属于一种双元变量问题。虽然某些题型可以直接带入暴力求解
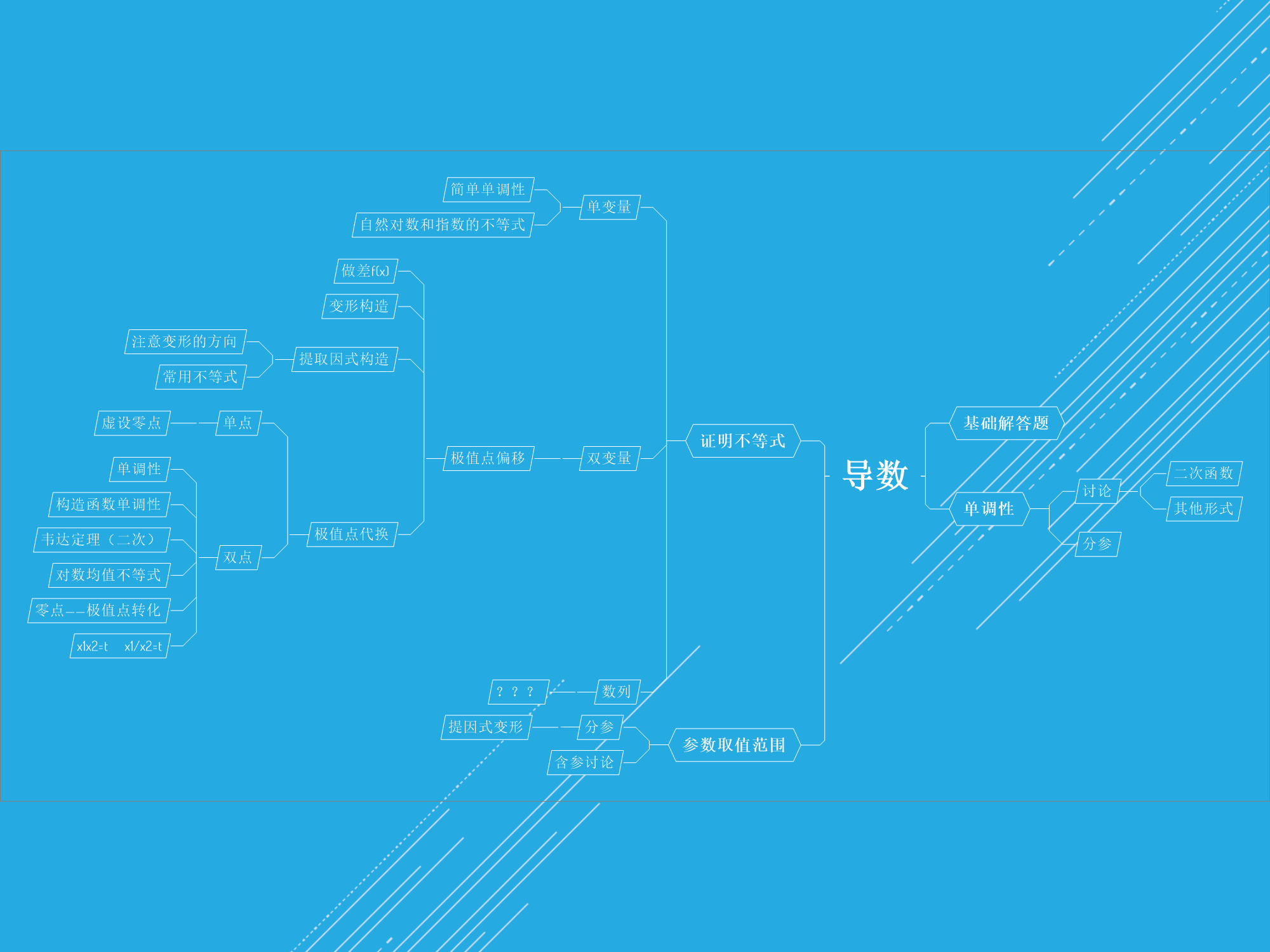
以一个例子来看
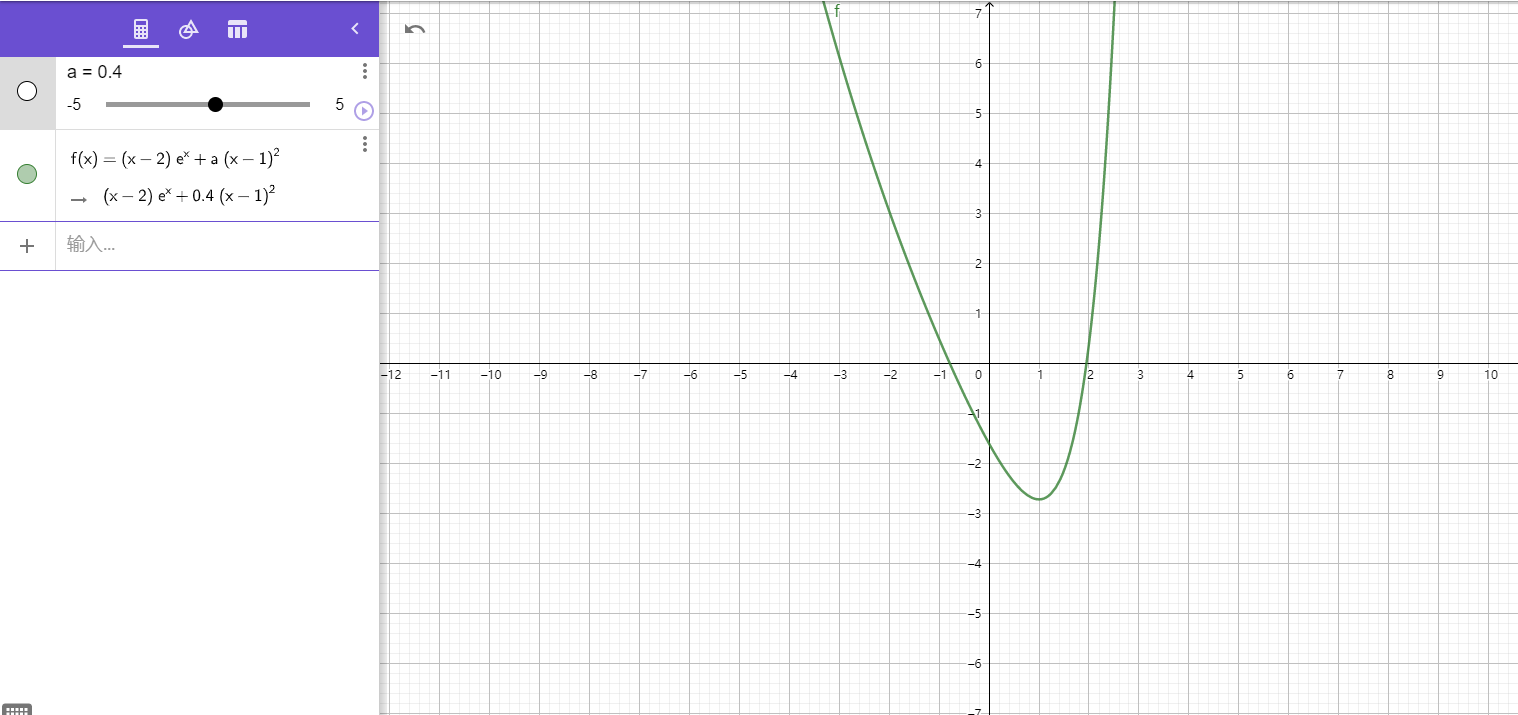
原本极值点为1,根据GGB的图像我们可以明显看到左零点到1的距离是大于又零点的,即(\(1>\frac{x_1+x_2}{2}\))此时我们称之为零点右偏,易得\(x_1+x_2<2\) ,我们要做的也就是证明这个式子。
关于这种问题的题设一般为以下四种形式
其中第四个解释一下,和第三个其实是一样的
求证\(f'(\frac{x_1+x_2}2)>0\)嘛,我们知道函数存在一个极值点,结合图像我们可以得到极值点左右的单调性,也就是(4)中\(x_0\)的位置,本质还是在求\(x_0\)和极值点的相对位置关系,也就是左右,这也是符合极值点题目的,可得到\(f'(x_0)\)的单调性。
均值不等式——从降分到跑路
对数均值不等式
要说到极值点偏移,我们就不得不解决一个最基本的的问题,就是关于\(lnx和e^x\)的问题,这里我们有一个基本的式子,他可以帮我们解决很多问题。
为啥会这样呢,从图像角度我们可以来理解
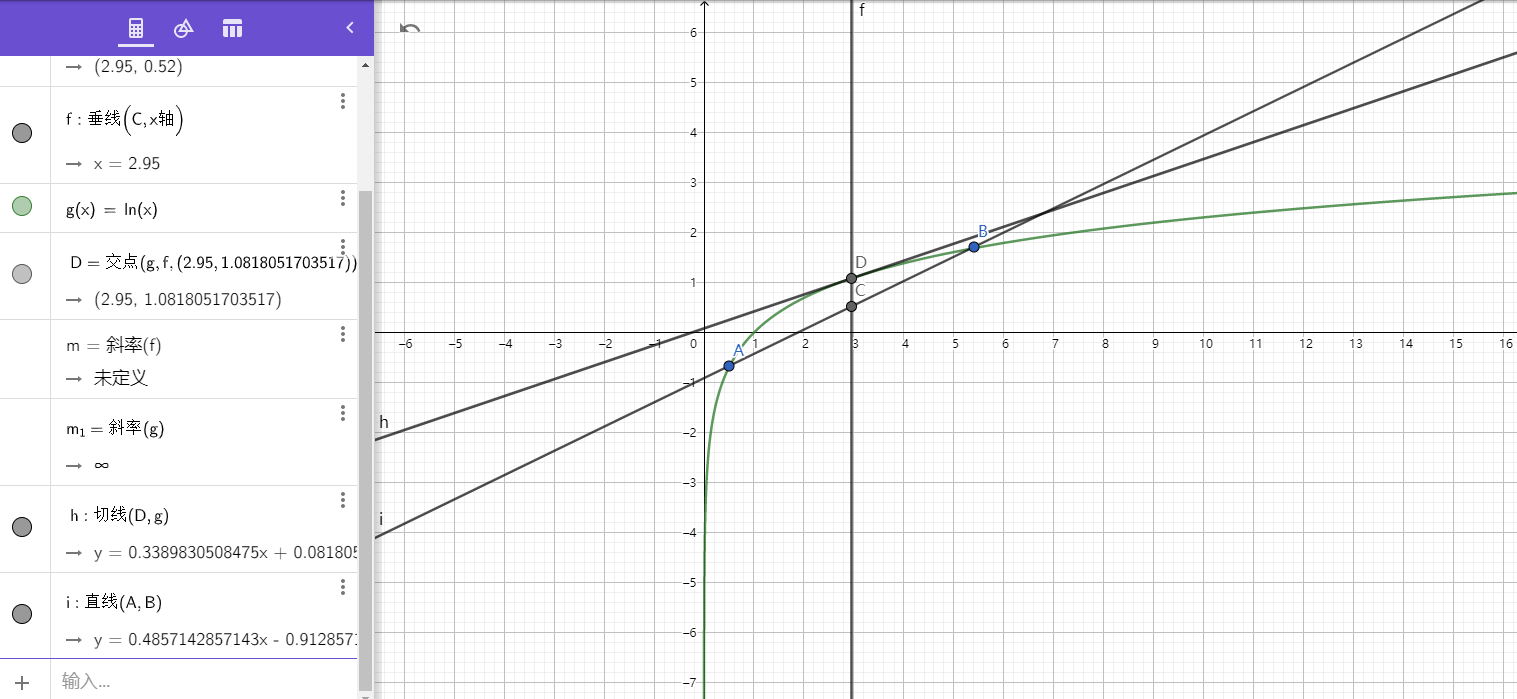
其中,\(A,B\)是函数\(f(x)=lnx\)上的两点,我们知道直线AB的斜率为\(\frac{lnx_1-lnx_2}{x_1-x_2}\),而D点(AB中点),也就是\(\frac{x_1+x_2}2\)点,它的切线斜率,我们通过移动AB两点,发现AB斜率是永远大于\(A,B中点x_0\)的,即我们说的
我们之前听过过拉格朗日中值定理

因为对数函数的倒数一开始增加的快,而往后增加的慢(具体看图像或者求导解决),所以它存在一个斜率等于直线AB的切线一定是在AB中点(设这个点为\(x_{卢本伟}\)前取的,即我们的AB中点的\(x\)坐标一定比\(x_{卢本伟}\)大,所以\(f'(x_{卢本伟})>f'(x_0)\)的,原式成立。
这也就是看看,上不了台面的,但我们可以看到它和极值点偏移特别像,我们完全可以证明出来。
处理双元变量的一般方法,要不就是整体代换,包括二次函数的话用韦达定理,对数的话直接构造不等式等等,要不就是消元,构造出\(t=x_1-x_2,t=\frac{x_1}{x_2}\)的式子,或可以先设一个函数为主元,类似于双元变量求最值,整体代换的话图像还差不多,那么我们可以通过消元。
证明:
首先设\(x_1<x_2\)
我们将其化为单元变量易得
单调递增,所以
即\(g(t)>0\)恒成立,原式得证。
同理右边的式子\(\frac{lnx_1-ln_x2}{x_1-x_2}<\frac1{\sqrt{x_1x_2}}\)也是可以通过变换,将函数化为关于\(\frac{a}b\)的函数的,证明过程差不多。
另外说一下,在这个式子中,对数位置上的\(x_1,x_2\)可以同时任意加减同一个常数,相应的,两个不等号两边的\(x_1,x_2\)也要同时加减一个相同常数,也是成立的
即
至于为啥底下的\(x_1,x_2\)没有减常数,自己去悟吧(这个式子下面绝对用不到)
为啥要证明这个式子呢,在做过题之后,包括构造函数题和极值点偏移,许多的设问都可以化成这种形式,然后化简证明就可以,当然这个式子也能推出其他的式子。
同样的,在证明过程中,我们也得到了另一个式子,可以用于对数的更精确的放缩调整
直观图像是这样的。
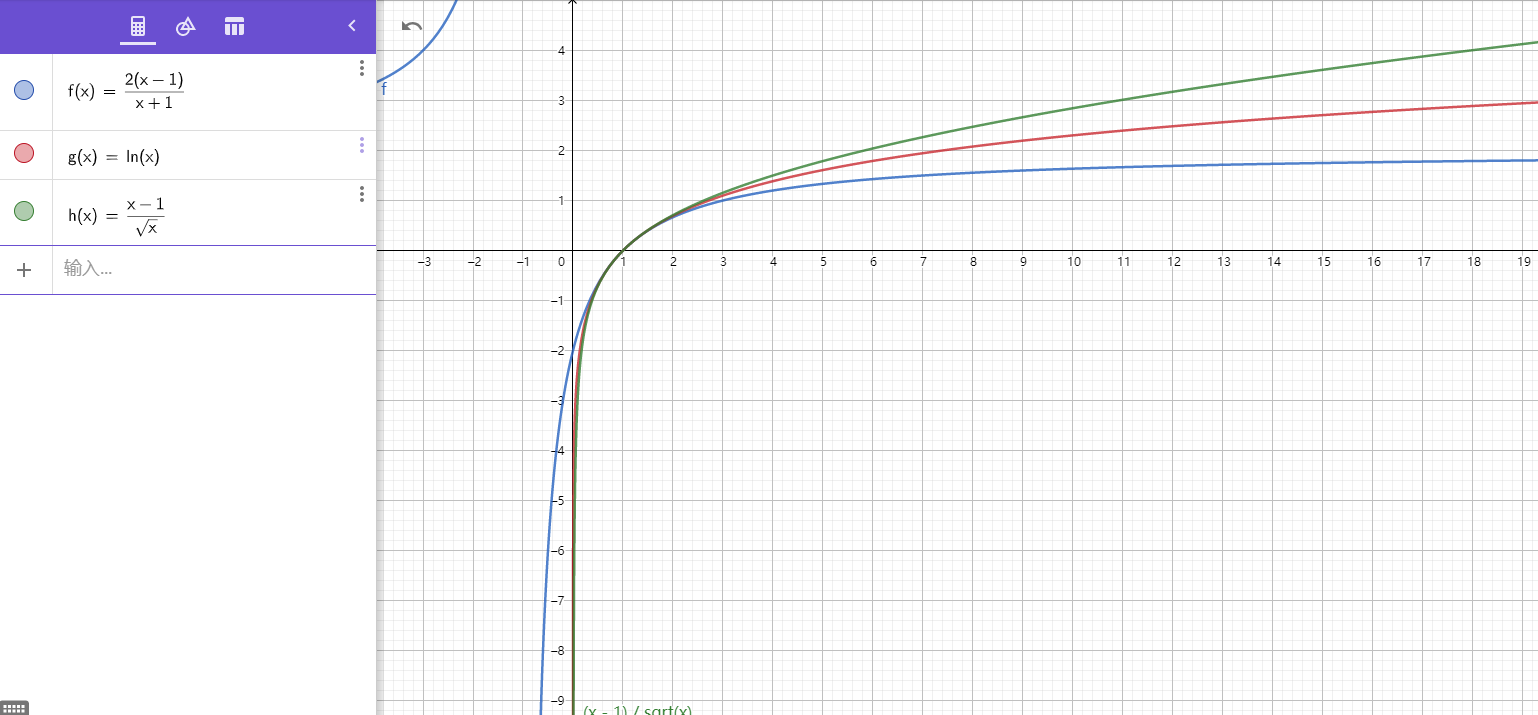
关于放缩的话有这么一个题
证明\(\sum\limits_{k=n+1}^{3n+1} \frac1k<\frac98\)
具体可以利用上面放缩得到\(ln(x+1)<\frac{2x}{x+2}\),令右边等于\(\frac1k\),求出\(x\),再将求得的\(x\)带入\(ln(x+1)\)进行裂项相消即可
练习:已知函数\(f(x)=lnx-x,f(x)=m\)有两个根\(x_1,x_2\),证明\(x_1x_2<1,x_1+x_2>2\)
证明:由题意得,\(lnx_1-x_1=lnx_2-x_2\)于是有
\[\sqrt{x_1x_2}<\frac{x_1-x_2}{lnx_1-lnx_2}=1<\frac{x_1+x_2}2,命题得证 \]
当然试卷上肯定不能写这么简单,起码要把上面证明的过程稍微写一下。
下面我们看一个极值点偏移的基本题型。
(2016全国I理21)已知函数\(f(x)=(x-2)e^{x}+a(x-1)^2\)有两个零点
(1)求\(a\)的取值范围;
(2)设\(x_1,x_2\)是\(f(x)\)的两个零点,证明:\(x_1+x_2<2\)
第一问由做题或者Geogebra图像得\(a>0\)
(2)\(f'(x)=(x-1)e^x+2a(x-1)=(x-1)(e^x+2a)\)
因为\(a>0\),函数只有一极值点,当\(x=1\)时,函数有最小值。
同时这也用到了处理极值点偏移的基本思路
- 求出函数的极值点\(x_0\)
- 利用对称性将一个零点转移到另一侧,\(eg:\)将\(x_1\)对称到\(x_0\)另一侧即为\(2x_0-x_1\)
- 利用函数单调性比较\(f(x_2)\)和\(f(2x_0-x_1)\)的关系
- 利用\(f(x_1)=f(x_2)\)化为关于单一变量的函数\(F(x)=f(x_1)-f(2x_0-x_1)\),结合定义域确定\(F(x)\)符号以便确定两者大小关系。
利用这个基本思路来解本题:
将\(x_1\)对称过去变为\(2-x_1\),即确定\(x_2\)与\(2-x_1\)关系
又因为\(f(x_1)=0\),所以
我们得到\(F'(1)=0\),当\(x<1\)时,\(F'(x)<0\),\(F(x)\)单调递减,且\(x_1\in (0,1)\)
\(F(x)_{min}<F(1)=0\),即\(f(x_2)<f(2-x_1)\),又有第一问图像得,\(f(x)\)在\((1,+\infty)\)上单调递增
这种常规题很多,解题方法也不唯一,可以化成对数等,但最重要的一点是要化简,尽可能化成一个求导比较容易或者代入后特别简单的式子。大多数的极值点偏移的题是和对数有关的,单独只有指数的题,也是有的,比如上题,许多含有对数的题最后通过整体代换可以可以化为上部分对数均值不等式的样子,像许多题目中含有\(\frac{f(x_1)-f(x_2)}{x_1-x_2}\)式子的,我们有很大可能可以通过整体带入来化简,或者化为单元变量,当然这也只是很大可能,具体情况也要具体分析。
下面是极值点偏移的另一种变形方法
已知函数\(f(x)=e^x-m(x-1)\)有两个零点,\(x_1,x_2(x_1<x_2)\),证明:\(x_1x_2<x_1+x_2\)
证明1:
\(f'(x)=e^x-m\)得到,零点是大于零的一个数,且函数先减后增,想要函数有两零点,\(m>0\),且\(f(0)=1+m>0\),所以,零点一定都大于零。(简单一写)最后真正解的话是有\(m>e^2\)的,此处解答省略
设\(t_1=\frac1{x_1},t_2=\frac1{x_2}\)
然后利用上面的对称化构造的方法证明\(t_1+t_2>1\)即可
需要注意的是,在这里,当\(t=1\)即\(x=1\)时式子是不成立的(本来人家\(x_1,x_2\)也不能等于0),但这并不会影响式子单调性的改变,因为底下是平方
所以,直接将\(t_1\)对称过去为\(1-t_1\)即可,利用上面讨论构造函数即可
证明2:
宁们看这样,我们有两个式子
我们给它相互一减,得到
woc,这个式子是不是在哪里见过?????我也不知道,但这个东西的大哥是这样的(之前的问题就是这么解决)
即\(x_1x_2-(x_1+x_2)+1<1\),原式得证
证明3:
既然我们从证明2中得到只需证明\((x_1-1)(x_2-1)>1\)即可
那根据证明2的两个式子我们得到只需证明
这个就不多说了吧,极值点为\(lnm\),按照一般对称构造即可,或者整体代换应该也能做。
已知 \(f(x)=e^x-ax\)有两个不同的零点\(x_1,x_2\),其极值点为\(x_0\).
求证:\(x_1+x_2>2\).
首先本题的极值点是含有未知量\(a\)的,并不会直接到2上去,所以我们要将其变形。
你们要知道(自带语音),这个零点不一定非要这个形式,反正\(x_1,x_2\)都是大于0的,既然这样我们可以将其变为导数不含有\(a\)的,以便求出其极值点。
求出\(g(x)\)极值点为1,过程省略就完事了,得到题目中的\(2x_0\),即2。
然后我们再根据\(g(x_1)=g(x_2)\),进行对称化构造进行证明即可。
本质上其实是一样的,其实这种方法我们可以通过一个图像直观来理解,我们使\(f(x)=0\),即\(\frac{e^x}x=a\)
函数的零点即等号两边图像的交点
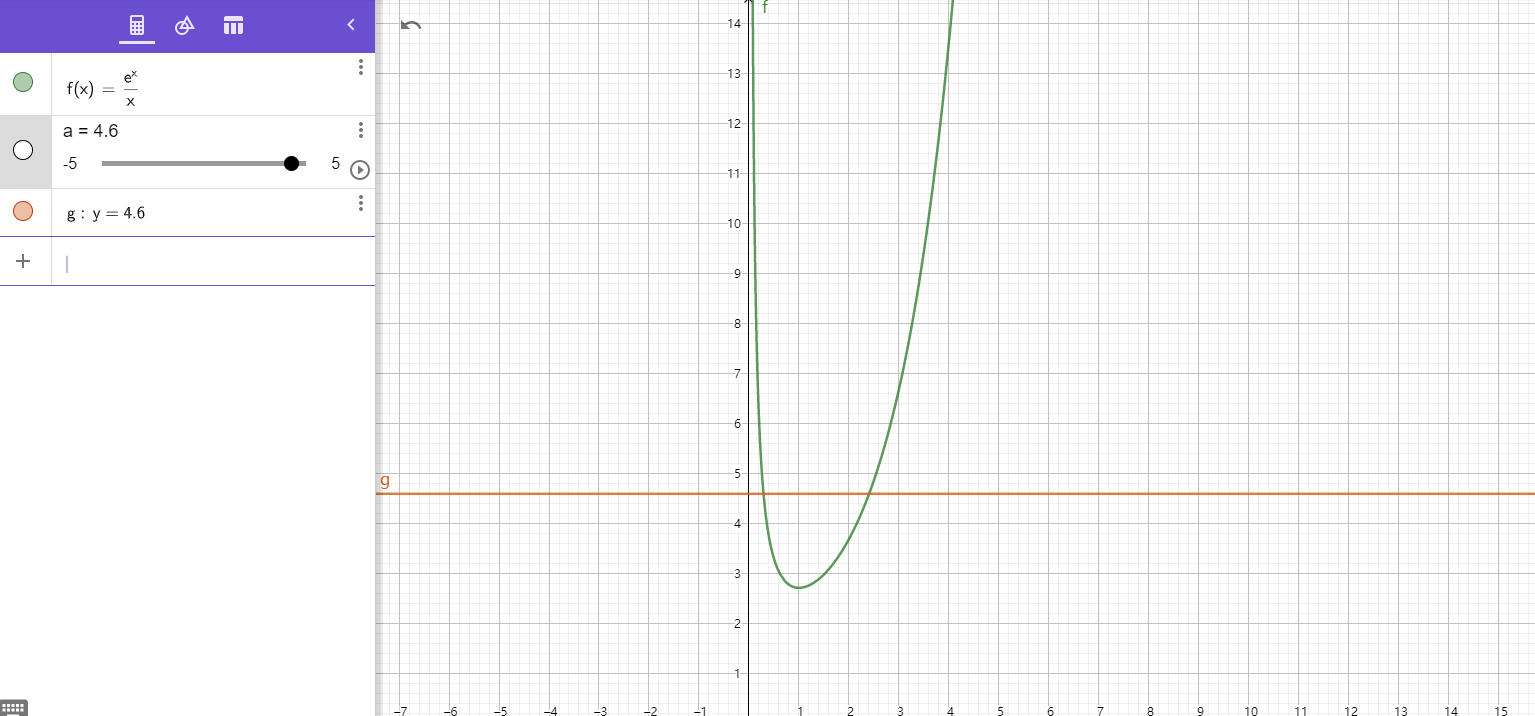
我们通过前面解题得到\(a>e\),即本题就可以转化为\(g(x)=\frac{e^x}x\),且\(g(x_1)=g(x_2)=a\)这种形式,和前面的证明也就一样
通过这个我们也可以知道,极值点偏移,不一定非要是极值点,零点,只要存在\(f(x_1)=f(x_2)\)或者其他关系,找出两个变量之间的关系再进行适当的化简,大部分题是这么个思路下面这个我不知道,不是大部分
《一月二十七日雨中读极值点偏移夜晚夜不能寐有感》
【民国】周先生
- 两点关系确定好,对称构造求个导
- 整体代入试构造,均值不等放开搞
- 双元变量难求导,构造消元要玩好
- 变量关系不好找,函数变化很重要
- 基础题型若练好,极值偏移算个鸟
- 考试题若难上雕,果断放弃睡个觉
最后留一个题目简单的题目,反正你让我做我是肯定做不出来。
已知\(f(x)=xe^{-x}\),且\(f(x_1)=f(x_2)\),其中\(x_1<x_2\),求证:\(2x_1+x_2>e\)
没了
参考文献
维基百科编者. 拉格朗日中值定理[G/OL]. 维基百科, 2019(20190722)[2019-07-22].
赖淑明. 极值点偏移问题的另一本质回归[J]. 中学数学教学参考, 2015 (4).

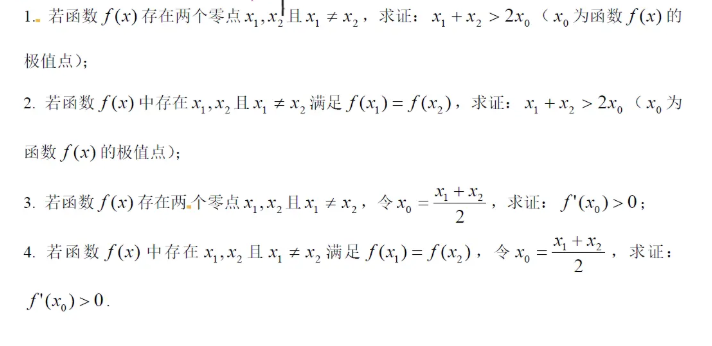

 浙公网安备 33010602011771号
浙公网安备 33010602011771号