结对开发之《返回一个二维整数数组中最大子数组的和》

一、题目要求

题目:返回一个二维整数数组中最大子数组的和。

要求： 输入一个二维整形数组，数组里有正数也有负数。 二维数组中连续的一个子矩阵组成一个子数组，每个子数组都有一个和。 求所有子数组的和的最大值。要求时间复杂度为O(n)。

结对编程要求： 两人结对完成编程任务。 一人主要负责程序分析，代码编程。 一人负责代码复审和代码测试计划。发表一篇博客文章讲述两人合作中的过程、体会以及如何解决冲突(附结对开发的工作照)。（截止到周四4月9日24:00）

 

二、编程思路

我们的思路比较简单，采用的是将子矩阵的和全部求出然后比较选出最大值的思路。大体思路确定了，主要就是如何求出以及怎样求出每个子矩阵的和。由于过程比较麻烦，以图片示意：

 

三、程序代码

#include<iostream>
#include<time.h>
using namespace std;
#define m 3  //m行数
#define n 3  //n列数

void main()
{
    int a[m][n],i,j,b[50];

    srand((int)time(0));

    //数组的值随机产生
    for(i=0;i<m;i++)
    {
        for(j=0;j<n;j++)
        {
            a[i][j]=-rand()%36+25;
        }
    }    
    
    //显示数组
    cout<<"矩阵如下："<<endl;
    for(i=0;i<m;i++)
    {
        for(j=0;j<n;j++)
        {
            cout<<a[i][j]<<'\t';
        }
        cout<<endl;
    }

    int c=0,d,e,f,sum=0,sum1=0;

    //计算所有子矩阵的值
    for(i=0;i<m;i++)
    {  
        for(f=0;f<n;f++)
        {
            sum=0;
            sum1=0;
            for(j=f;j<n;j++)
            {
                sum+=a[i][j];
                b[c]=sum;
                c++;

                sum1=sum;
                for(d=i+1;d<m;d++)
                {
                    for(e=f;e<=j;e++)
                    {
                        sum1+=a[d][e];
                    }
                    b[c]=sum1;
                    c++;
                }
            }
        }
    }

    int max;
    max=b[0];
    for(i=0;i<c;i++)
    {
        if(b[i]>max)
        {
            max=b[i];
        }
    }

    cout<<"该矩阵最大子矩阵的值为："<<max<<endl;
}

 

四、运行结果截图

 

 

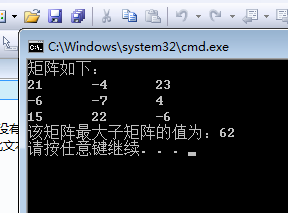
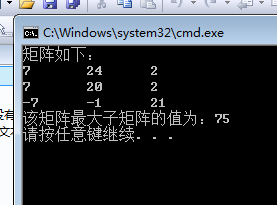
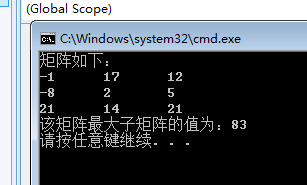
五、工作照

 

六、总结

       这次我主要负责编写代码，康娜同学负责代码的复审和测试。编写代码的时候要拿一张白纸想到什么方法或者思路就写下来，一定要先把逻辑思路想清楚在开始编，否则循环部分的代码就很容易编乱套。另外就是书写方面，按照上课的代码规范书写，每一个if或for语句不管下面有几条语句都要加大括号，这样看起来比较清晰好看。这次试验编写代码比较麻烦，但是代码的测试我感觉也不轻松，要一个一个的算，很复杂。我觉得两个人合作完成，各有各的明确分工，减轻了工作量，也提高了工作的效率，有条不紊。