C语言汉诺塔算法原理分析与实践
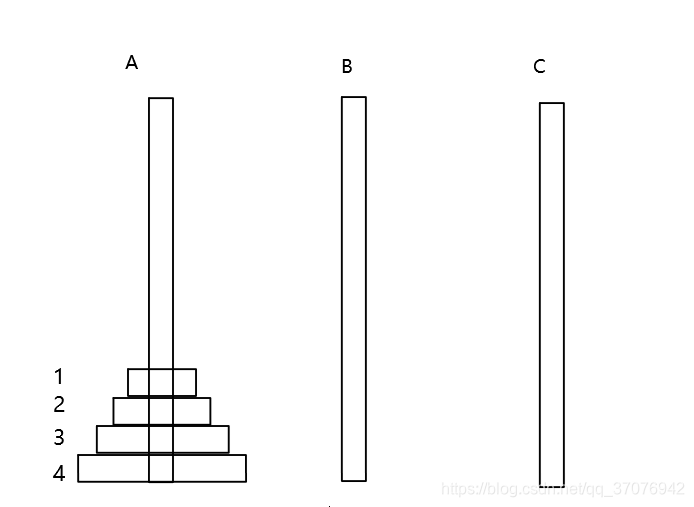
汉诺塔游戏的规则:如下图所示,有三个柱子A,B,C,我们要做的是把A柱的所有圆盘,全部转移到C柱上,转移时遵循的规则如下:
1、每次只能移动一个圆盘
2、所有的大圆盘必须在小圆盘的下面
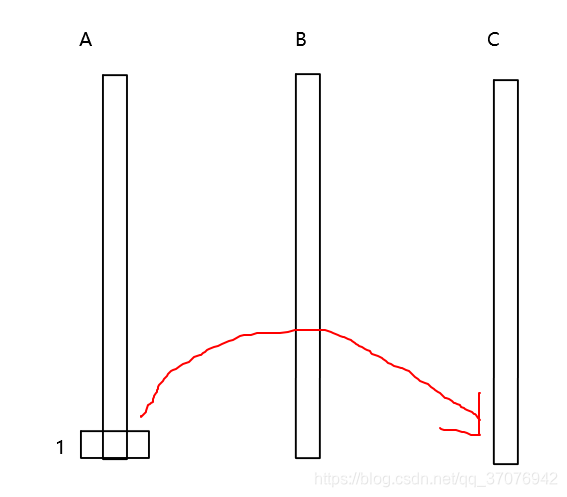
首先假设只有一个圆盘,我们将其编号为1,如下图所示,那么这时候只需要将A直接移到C即可:
当存在多个圆盘时:我们以三个为例观察现象
首先三个圆盘放在A柱上,按从上到下的顺序依次编号为1,2,3(最小的为1,最大的为3),我们先不考虑3号盘,而只考虑上面两个小一点的圆盘(编号1,2),而此前我们已经分析了两个圆盘的移动过程,那么这两个圆盘该移动到哪根柱子呢?目前只有B柱,C柱可选,而C柱肯定不行,因为C柱是目标柱,那么我们只能把1,2号盘从A柱移动到B柱,借助C柱,则移动过程为:A->C, A->B,C->B。此时,1,2号盘已经到达B柱,再把最大的三号盘,直接移到C柱。此时工作快要完成了,目前的状态为:1,2号盘在B柱,3号盘已到达目的柱C柱,再接下来,把1,2号盘将B柱移动到C柱,转移工作就彻底结束,借助A柱,转移过程为:B->A,B->C,A->C。
函数定义
根据上面的分析,我们知道,函数的参数,有盘子,A,B,C三个柱子,所以,函数的签名为: func(n, a, b, c)。其中n表示圆盘的个数,a表示起始柱,b表示辅助柱,c表示目标柱。
def func(n,a,b,c):
if n == 1:
print(a,"-->",c)
else:
func(n-1,a,c,b)
print(a, '-->', c)
func(n-1,b,a,c)
if __name__ == '__main__':
func(4,'a','b','c')
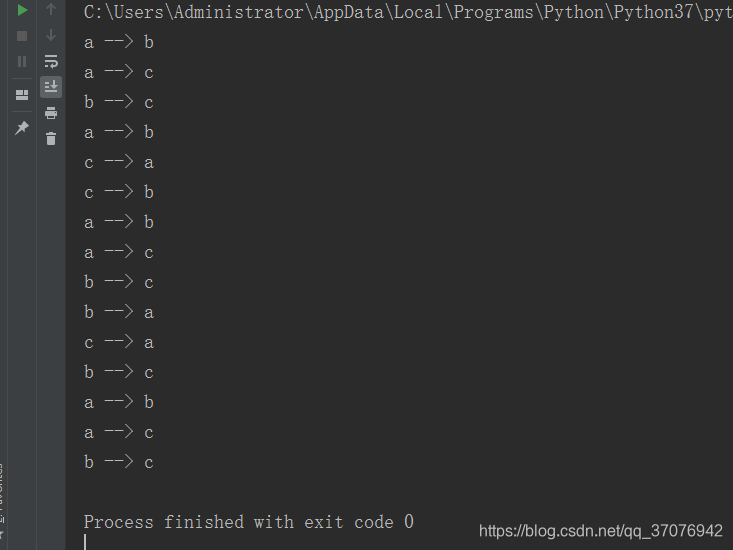
可以将代码理解为三个步骤:
func(n-1,a,c,b)
第一步:该递归是将A柱上n-1个圆盘借助c移动到b
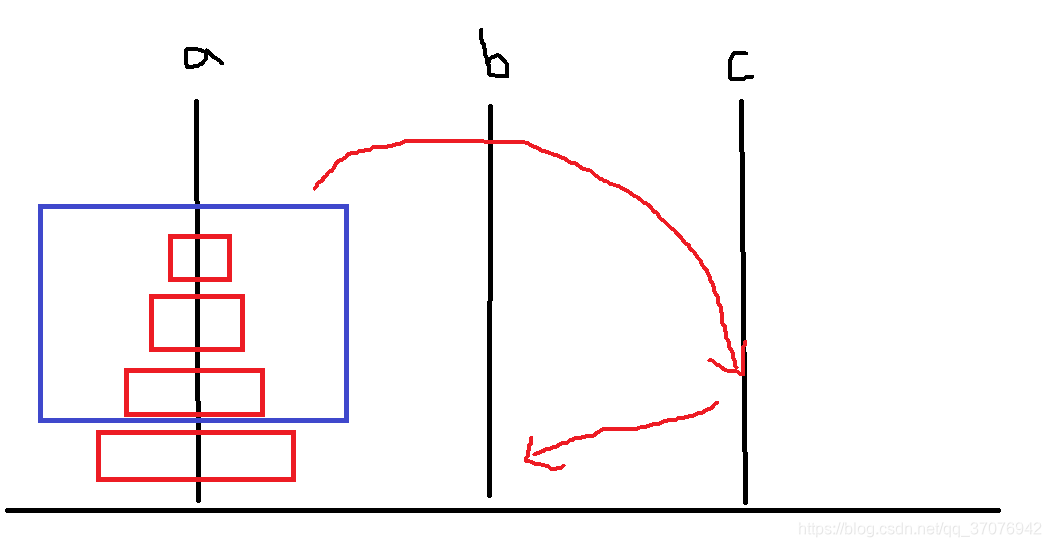
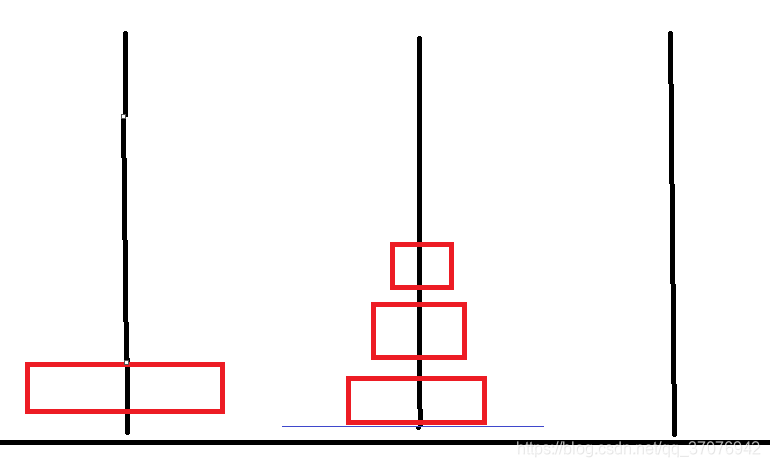
print(a, '-->', c)
第二步:将第n个圆盘从a移动到c
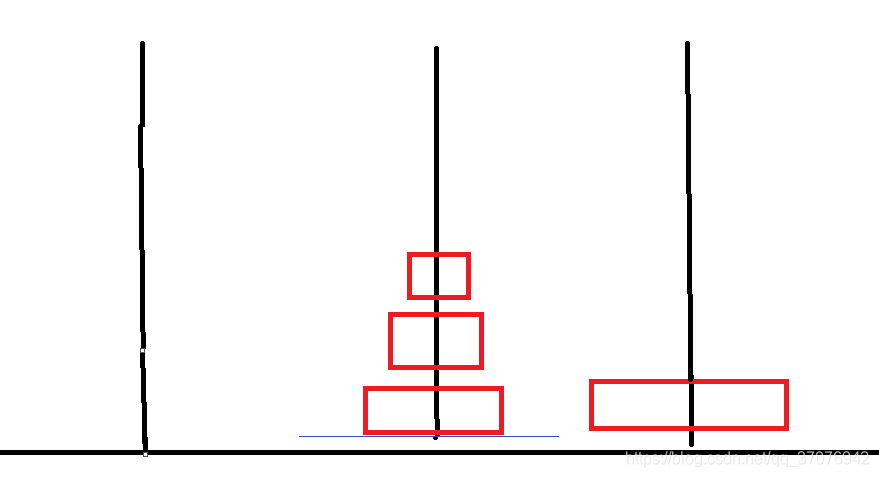
func(n-1,b,a,c)
第三步:该递归将b柱上n-1个圆盘借助a移动到c
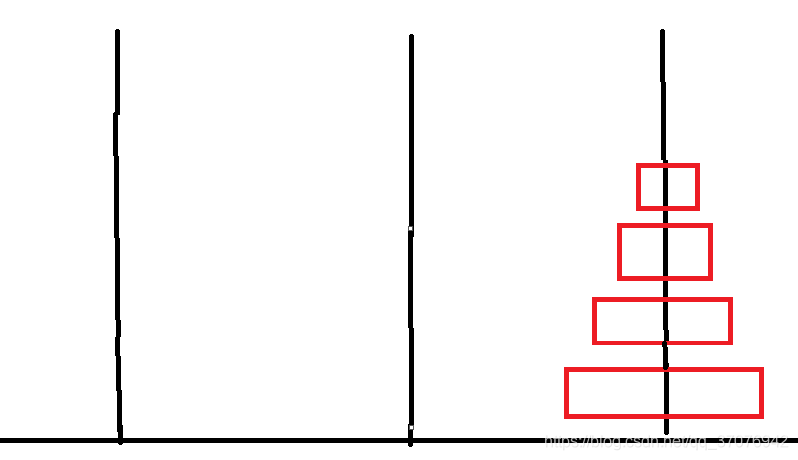
扩展:
C语言写汉诺塔递归算法
#include <stdio.h>
#include <windows.h>
void Hanoi(int n, char a,char b,char c);
void Move(int n, char a, char b);
int count;
int main()
{
int n=8;
printf("汉诺塔的层数:\n");
scanf(" %d",&n);
Hanoi(n, 'A', 'B', 'C');
Sleep(20000);
return 0;
}
void Hanoi(int n, char a, char b, char c)
{
if (n == 1)
{
Move(n, a, c);
}
else
{
Hanoi(n - 1, a, c, b);
Move(n, a, c);
Hanoi(n - 1, b, a, c);
}
}
void Move(int n, char a, char b)
{
count++;
printf("第%d次移动 Move %d: Move from %c to %c !\n",count,n,a,b);
}



