Cadence DSP 算子开发上手指南
作者:洪超 | 旷视科技 MegEngine 架构师
前言
Cadence 的 Vision P6/Q6/Q7 系列 DSP 在很多的 ISP (“Image Signal Processor”) 芯片中都有部署,可以在图像处理场景补充甚至碾压 CPU 算力。而且 Cadence 官方提供了一个比较全的基础算子库 libxi,很多标准算子在 libxi 中都有特定参数组合下的参考实现。但是鉴于 Cadence DSP 开发群体比较小,网络上能找到的中文资源几乎没有,从零进入开发状态的门槛还是不低的。本文梳理了一些 Cadence DSP 算子开发中的重点,希望可以给对 Cadence DSP 开发有兴趣的同学带来帮助。
DSP 架构特点
首先,以 Cadence 的 Q7 为例,介绍一下 DSP 架构上的特性。下图是 Q7 硬件架构的简化。
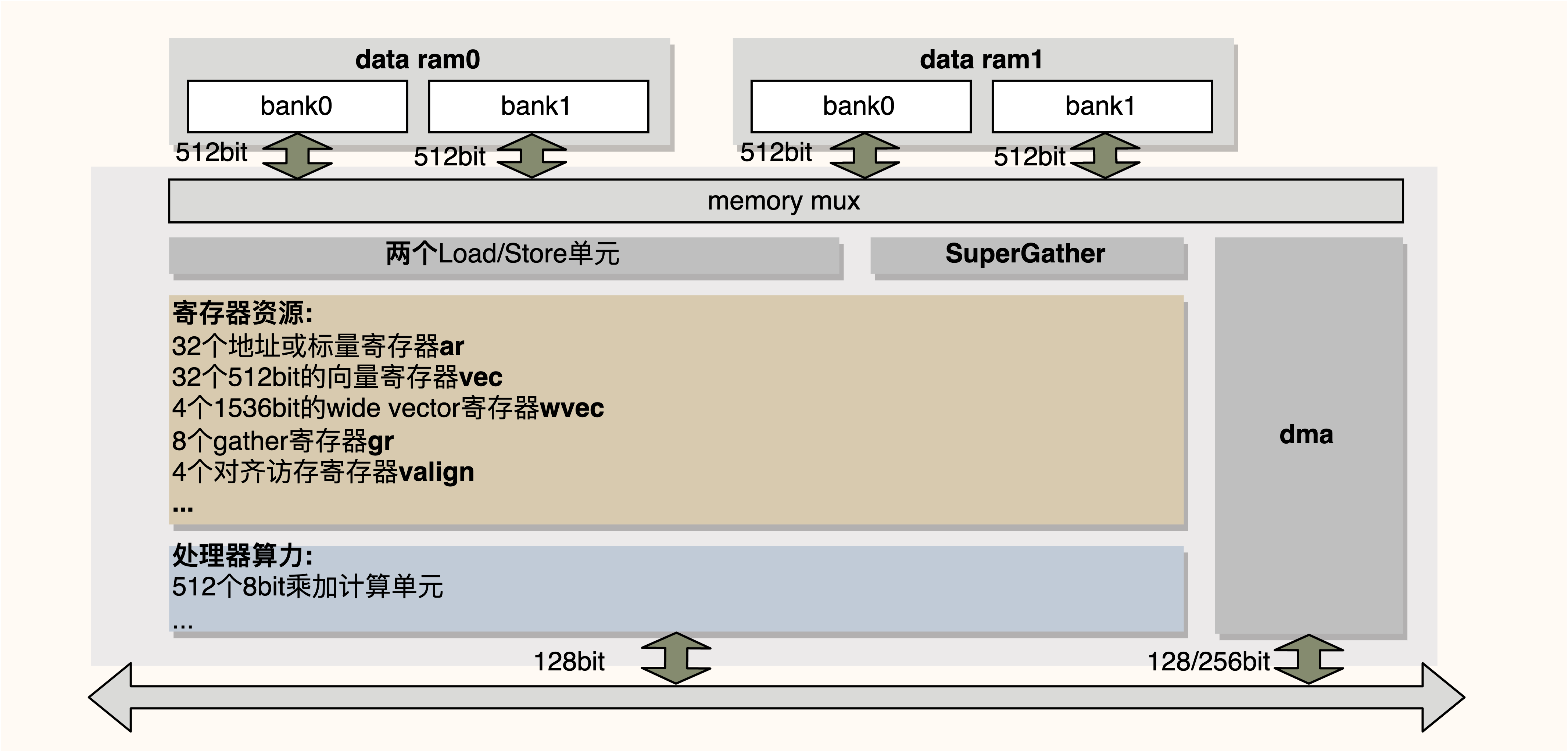
从图中可以直观的得到 DSP 处理器的算力、寄存器等信息,注意 DSP 上有两块 data ram(简称 dram),每一块 dram 又分为两个宽为 512bit 的 bank。同时,DSP 上有两个 Load/Store 单元,Load/Store 模块访问 dram 的带宽都是 512bit,所以理论上的访存带宽是 1024bit/cycle,而独立于 Load/Store 的 SuperGather 模块是为了支持 DSP 上高效的 gather/scatter 操作。另外,可以看到 DSP 还有一个 dma 模块,该模块用于片外空间和 dram 之间的数据传输。
为了充分利用算力和访存能力,Cadence DSP 支持了 SIMD(Single Instruction, Multiple Data) 和 VLIW(Very Long Insruction Word) 两种特性。前者支持 64lanes * 8bit 或 32lanes * 16bit 等总位宽为 512bit 的向量访存和向量计算,后者是一种谋求指令级并行 (ILP, instruction level parallelism) 的技术。VLIW 可以将多个指令打包后在一起同时发射,从而获取指令级的并行度。与超标量、乱序执行等其他 ILP 技术不同的是,VLIW 的并行指令排布是在编译期就确定好的,而不需要 CPU 进行复杂的运行时调度。VLIW 使得 DSP 处理器在不需要大幅增加硬件复杂度的情况下,就可以获取 ILP 的加速收益。
还要补充一点,Cadence DSP 是哈弗架构,其指令和数据独立编址,具体的编址规格由 LSP(Linker Support Package) 决定,而用户可以通过名为 memmap.xmm 的内存配置文件来定义和修改 LSP。截取了一段 xmm 文件的内容,简单注释如下:
// 存指令的地址段
BEGIN iram0
0xe000000: instRam : iram0 : 0x8000 : executable,writable ;
iram0_0 : F : 0xe000000 - 0xe007fff : .iram0.literal .iram0.text ...
END iram0
// 256k 的 dram0
BEGIN dram0
0xe080000: dataRam : dram0 : 0x40000 : writable ;
dram0_0 : C : 0xe080000 - 0xe0bffff : .dram0.rodata .dram0.data .dram0.bss;
END dram0
// 240k 的 dram1
BEGIN dram1
0xe0c0000: dataRam : dram1 : 0x3c000 : writable ;
dram1_0 : C : 0xe0c0000 - 0xe0fbfff : .dram1.rodata .dram1.data .dram1.bss;
END dram1
// 16k 的栈空间,创建在 dram1 的尾巴后面
BEGIN dram1_stack
0xe0fc000: dataRam : dram1_stack : 0x4000 : writable ;
dram1_stack : C : 0xe0fc000 - 0xe0fffff : STACK : ;
END dram1_stack
// 存 os 相关的地址段
BEGIN sram0
0x10000000: instRam : sram0 : 0x2000000 : executable,writable ;
sram0 : F : 0x10000000 - 0x11ffffff: HEAP : .sram.rodata .rtos.data
END sram0
从注释中我们可以看出,xmm 文件规定了运行时的数据、指令、栈、os 等各部分的地址范围。
算子调用流程
有了上一节的背景知识,我们来感性地了解下一个 DSP 算子是如何被调起来的。
我们从 CPU 侧发起调用,通过 rpc 协议调起 DSP 侧提供的服务,将 CPU 侧程序称为 rpc_host,而 DSP 侧程序称为 rpc_dsp。rpc_dsp 负责起一个线程监听来自 rpc_host 的 message,并从 message 解析出需要进行的动作,并在执行完该动作后回复 rpc_host 一个 message。我们需要预先将 rpc_dsp 编译成可执行程序,再将可执行程序 dump 成 bin 文件,这里称为 dsp_bin(包含 iram.bin 和 sram.bin)。而 CPU 侧负责准备算子调用的所有输入,并装载编译好的 dsp_bin 到 DSP 的 dram 中(前文介绍 LSP 的部分有说明应该如何进行内存映射),同时把 rpc_dsp 侧的监听线程 run 起来,最后 rpc_host 发起 rpc 调用并等待 rpc 返回。
需要说明一点,CPU 和 DSP 之间一般会使用 IPCM(核间通信模块)实现对一段 ddr 地址空间的共享。但是 DSP 直接访问这段 ddr 的延迟是远大于访问 dram 的延迟,所以对于算子执行过程中需要频繁访问的 ddr 数据,一般是先使用 dma 将其搬运到 dram 上,算子执行结束后,计算的输出再通过 dma 搬回到 ddr。
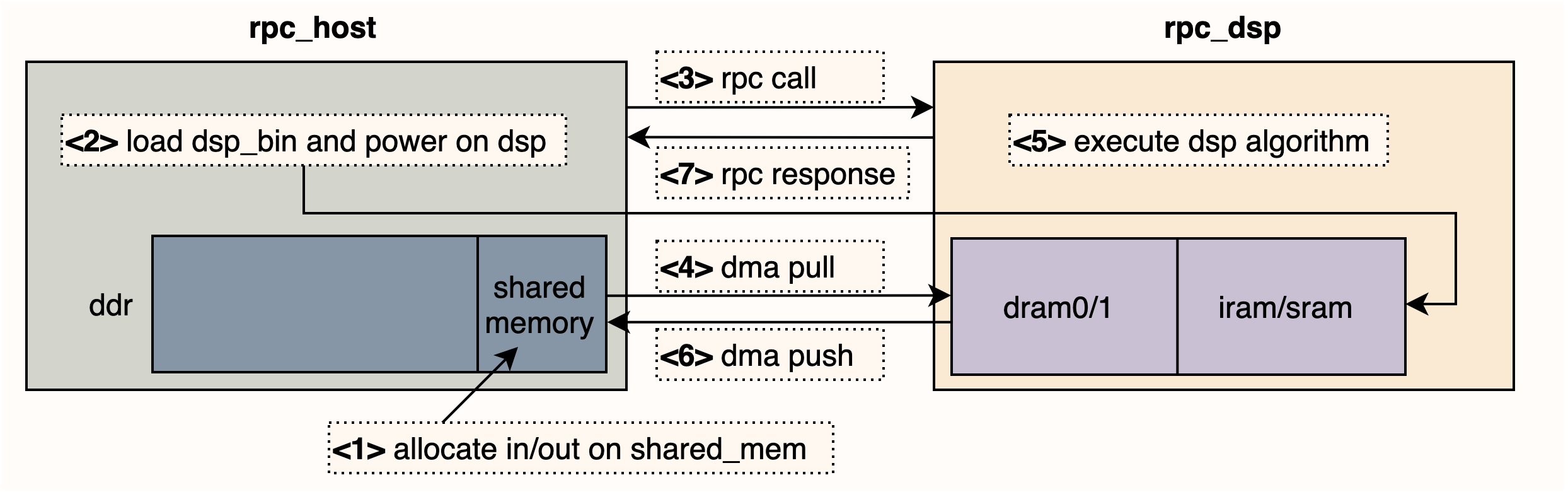
以上就是算子调用流程的概述,搭配了一张时序图,图中用虚线框标出了具有时序关系的若干步骤,如下所示:
工具链介绍
Cadence 为 DSP 开发者提供了 Xtensa 开发包,里面包含了一整套编译、链接、执行、调试等相关的命令行工具。这些命令用法上很类似 GUN 的标准工具,而 Cadence 主要是加强了编译的部分,因为前面提到 Cadence DSP 使用 VLIW 进行加速,而 VLIW 技术要求编译器做更多的事情,来尽可能获得一个更优的编译期指令排布。
上一节讲述的调用流程是在 DSP 硬件上跑算子的流程,看上去不是很友好。好在 Xtensa 工具包里还提供了 Cadence DSP 的模拟器,使用 xt-run 命令就可以在模拟器中执行算子,从而使得开发验证、性能调试都可以脱离真实的硬件。
下面就以"hello world"为例,介绍一下命令行工具的使用:
// file: hello_world.c
#include <stdio.h>
int main() {
printf("hello world\n");
return 0;
}
编译:
xt-xcc hello_world.c -o hello_world.bin
不带内存模型执行,用于算子初版实现,不模拟访存延迟:
xt-run ./hello_world.bin
带内存模型执行,仿真性能非常逼近 DSP 硬件上的速度:
xt-run --mem_model ./hello_world.bin
带--summary 选项执行,可以对 cycle 分布有一个统计结果,比如 retaired inrstuction、branch delay、cache_miss 等各部分的 cycle 占比:
xt-run --summary ./hello_world.bin
如果需要 gdb 调试的话,可以用 xt-gdb:
xt-gdb ./hello_world.bin
如果需要 profiling 的话,需要先在执行期加--client_cmds="profile --all gmon.out 选项,用于在当前目录下生成各种 profiling 文件,包括 gmon.out.cyc, gmon.out.bdelay, gmon.out.interlock 等,然后使用 xt-gprof 工具查看上一步生成的 profiling 文件,比如执行下面两行命令就可以查看函数级别的 cycle 分布:
xt-run --client_cmds="profile --all gmon.out" ./hello_world.bin
xt-gprof ./hello_world.bin ./gmon.out.cyc > hello_world_cyc.txt
分块计算
Cadence DSP 主要应用场景是图像处理,现实的业务中图片尺寸经常都是 1080P 甚至 4K 的分辨率,而 DSP 的 dram 容量虽然可配置,但是通常都是 200KB 左右的级别(壕配十几兆 dram 的是例外),根本放不下一张大图,这就是导致了我们的算子必须分块计算。通过将大图分成一个个小块(tile), 每次通过 dma 从 ddr 搬运一个 src_tile 到 dram 上,执行算子得到一个 dst_tile, 再通过 dma 把 dst_tile 搬到 ddr 上。
认识 tile
拿一张图说明一下 tile 的具体参数:
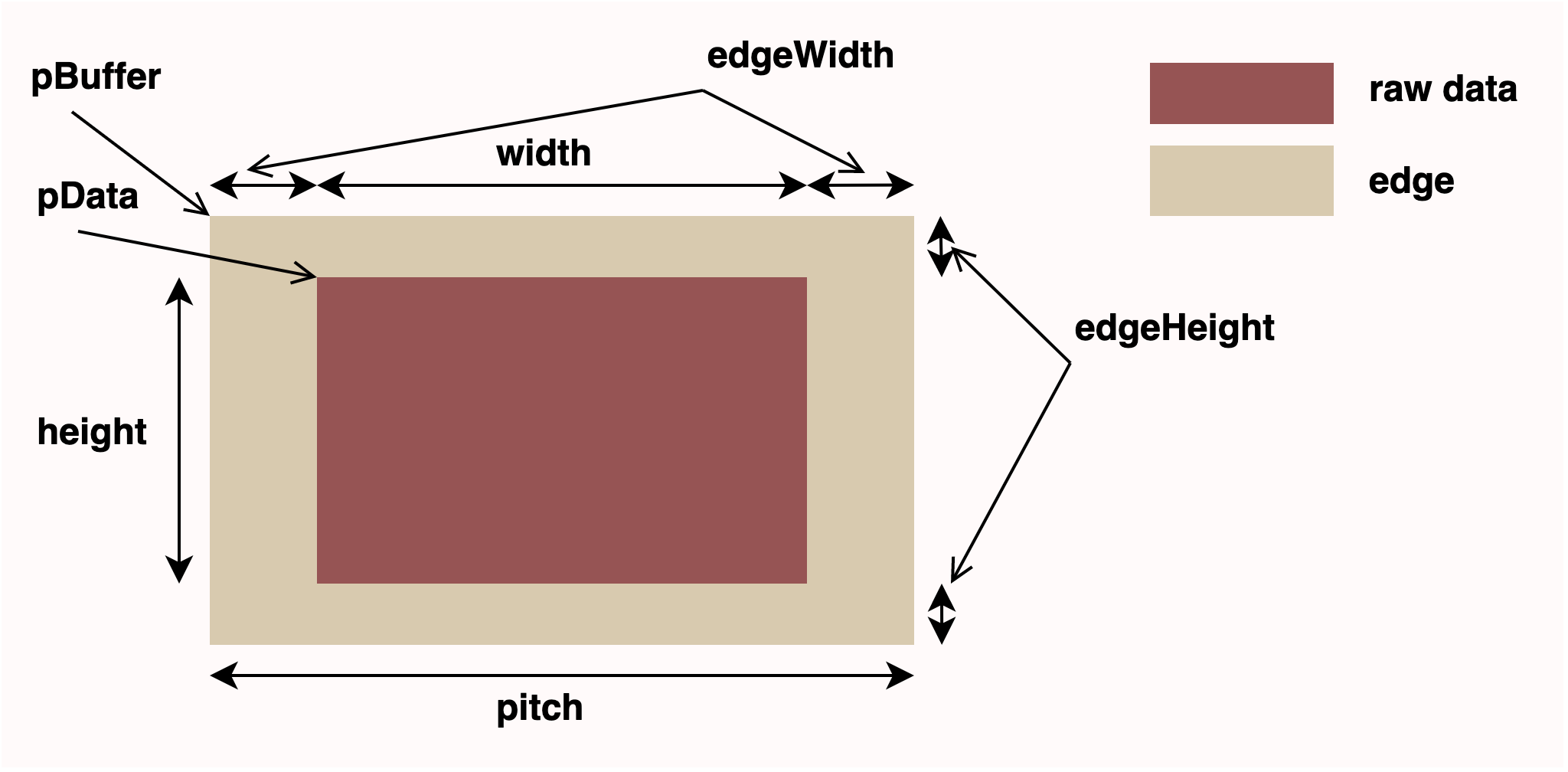
可以看到 tile 分两层,里层的红色区域是原始数据区域,尺寸即 tile_width*tile_height, 外层是一圈 edge, 因为有些算子操作,比如 filter2d,计算的时候需要 padding,edge 的尺寸即为 padding 的大小。也正是因为 edge 的存在,才有了 pData 和 pBuffer 的区分。
dram 内存管理
tile 是分配在 dram 上的,就是 xmm 文件中的 dram0 和 dram1 段,dram 是我们自由使用的,所以就需要一个内存管理的逻辑。
首先定义一个数据结构 DramCtrl:
struct DramCtrl {
char* dram_start; // xmm 文件中 dram0/1 的起始地址
char* dram_end; // xmm 文件中 dram0/1 的终止地址
char* dram_cst_use; // 算子开发中可以自由使用的起始地址
char* dram_free; // 当前尚未分配区域的起始地址
char* dram_idx; // 区分不同 dram 段的索引
};
其中 dram_cst_use 参数的存在是因为有些变量必须分配在 dram 上,但是在调用不同算子的时候不需要更新,表现出一定的持久性。这种变量就包括 DramCtrl 本身,还有 dma 用于定义传输任务的 descriptors,所以刨掉这部分变量占用的空间,从 dram_cst_use 位置开始的 dram 才是算子调用自由使用的空间。
有了数据结构之后,还需要定义一些接口函数,才能满足基本的管理需求:
void dram_init(): 在 DSP 开机后,调用第一个算子前,执行 dram_init,初始化 DramCtrl 结构体,dram_cst_use=dram_free=dram_start+sizeof(DramCtrl)
void dram_static_alloc(): 在 dma_init 调用之后,分配 dma 的 descriptors,dram_cst_use+=sizeof(descriptors), dram_free=dram_cst_use
void dram_free_size(): 查询当前还有多少空闲内存,返回的是 dram_end-dram_free
void dram_alloc(sz): 分配 tile 等变量的空间,先 check 空闲空间大小,分配成功后修改 dram_free+=sz
void dram_reset(): 在一次算子执行结束后调用,重置 dram_free=dram_cst_use
pingpong dma 搬运
dma 完成一次 tile 搬运的延迟是相当可观的,如果 dma 搬运与算子调用是串行执行的话,性能就会严重受累于 dma 的搬运。所以正确的做法是,借用 pingpong buffer 的概念,在计算当前 tile 的同时,进行下一个 tile 的预取,这样 dma 搬运的时间就可以被计算时间隐藏。基于 pingpong dma 的算子执行逻辑如下:
step 0. dram_alloc src_tile[2], dst_tile[2] and set pingpong = 0
step 1. dma pull src_tile[pingpong]
step 2. dma sync, make src_tile[pingpong] be ready on dram
// loop begin ->
loop_for (h = 0; h < image_height; h += tile_height)
loop_for (w = 0; w < image_width; w += tile_width)
step 3. prefetch, using dma pull src_tile[pingpong^1]
step 4. exec on src_tile[pingpong] to get dst_tile[pingong]
step 5. dma sync, sync for last iter dma push and this iter prefetch
step 6. dma push dst_tile[pingong]
step 7. pingpong = pingpong^1
// loop end <-
step 8. dma sync & dram_reset
分块逻辑
现在,我们已经认识了 tile 的概念,有了简单的 dram 内存管理,以及 pingpong dma 搬运和计算并行的逻辑,但是还缺了一块儿:分块逻辑。分块就是在 dram 容量的约束条件下,依据 src_tile 和 dst_tile 的尺寸关系确定 tile 的尺寸。其实没有普适的分块逻辑,很多时候都是具体问题具体分析,这里笔者根据开发经验给出三种分类:
- 第一类:src_tile 和 dst_tile 尺寸一致
比如 elelwise 类和 filter 类,elemwise 类算子输入输出的尺寸是完全一样的,filter 类只比 elemwise 类多了一圈 tile_edge。这一类算子的 tile 尺寸很好确定:假定算子的输入输出 image 个数之和为 inout_cnt,且 tile_width 等于 tile_height,则有
tile_w=tile_h=srqt(min_dram_sz / inout_cnt)
其中,min_dram_sz 是取两个 dram 容量的小值,因为 pingpong dma 的需要,实际分配的 tile 总数是 inout_cnt * 2。
- 第二类:src_tile 和 dst_tile 的尺寸不相等,但是有明确的相对关系
比如 resize 算子,src_tile 和 dst_tile 的尺寸不再是一样的,但是缩放比例 scale_x 和 scale_y 决定了 tile 的尺寸关系:
dst_tile_w=dst_tile_h=srqt(min_dram_sz / (1.0 + scale_x * scale_y))
src_tile_w=dst_tile_w * scale_x
src_tile_h=dst_tile_h * scale_y
- 第三类:src_tile 和 dst_tile 没有明确的尺寸关系
比如 warp_perspective 算子,因为一个矩形的 dst_tile 通过 warp_perspective 映射到 src_image 上,得到的是一个凸四边形,需要框出这个凸四边形的 bounding_box 作为 src_tile。另外,很重要的一点,相同尺寸不同坐标位置的 dst_tile 映射得到的 src_tile 尺寸也是不一样的。为了保证 dst_image 中所有 dst_tile 映射得到的 src_tile 在 dram 中都能放得下,就需要一个搜索策略来确定 tile 的尺寸:
int guess_tile_size(min_dram_sz, frame) {
int l = 0, r = sqrt(min_dram_sz);
while (l <= r) {
int mid = (l + r) / 2;
int ret = 0;
ret = iter_warp_perspective(mid, frame);
if (ret < 0)
r = mid - 1; // ret < 0 表示当前尝试的 dst_tile 的尺寸会使得 src_tile 在 dram 上放不下,所以可行域直接减半
else
l = mid + 1; // ret = 0 表示当前尝试的 dst_tile 的尺寸是 ok 的,但是继续尝试更优解
}
if (r < 0) {
LOG(ERROR, "get tile size failed %d\n");
return -1;
}
LOG(DEBUG, "get the best guess tile width %d\n", r);
return r;
}
其中,frame 里存的 dst_image 的整图尺寸,iter_warp_perspective 里的逻辑就是遍历 dst_image 各个坐标位置的 dst_tile,通过 warp_perspective 的映射矩阵反算出 src_tile 的 bounding_box 的大小,并检查 dram 是否放得下。如果所有位置的 check 都通过了,iter_warp_perspective 返回 0,反之返回-1。
ISA 介绍
先插播一段语法介绍,Cadence DSP 上的 SIMD 指令大体由四部分组成:prefix_op_size_suffix。第一部分的指令前缀都是 IVP(image vector prcessing); 第二部分就是具体运算指令的名称缩写,如 ADD,MUL,SEL 等;第三部分是指定向量中的通道关系,比如是 64lanes * 8bit 还是 32lanes * 16it,不过前者实际写成 2NX8, 后者写成 NX16,因为在这里 N 表示 32; 第四部分是一些后缀的修饰词,比如 U 表示一元运算的数据是无符号数,US 表示二元运算的数据分别是无符号数和有符号数,T 表示该运算会带 mask, PACK 表示该运算会对中间计算结果做位压缩再返回较窄的数据类型,等等。
现在放几条简单的 SIMD 指令,让大家对号入座,温故一下:
IVP_ADDNX16: 32lanes * 16bit 有符号整数的加法运算
IVP_MUL2NX8U: 64lanes * 8bit 无符号整数的乘法运算
IVP_LV2NX8U_I: LV 表示 vector load, _I 后缀在这里是表示有一个立即数(immediate)的 offset,该命令是在一个 64byte 对齐的地址(base_ptr + offset)上 load 64lanes * 8bit 的数据
考虑到介绍 ISA 是比较枯燥的,而且很多人对 CPU 上的 SIMD 指令都有一些了解,所以这里只展开介绍四组较于一般的 SIMD 实现有一些不同点,同时使用频率非常高的指令。
第一组:带指针自动对齐、自动偏移以及支持可变长度的 VLOAD 指令
Cadence DSP 要求 VLOAD 访问不可以跨 bank,而 bank 的位宽是 512bit,也即限制了 VLOAD 的地址必须是 64byte 对齐的。如果地址满足对齐要求,就可以使用 IVP_LVxxx 指令直接进行访存操作,反之就需要使用 IVP_LAxxx 指令进行指针自动对齐的访存操作:
void IVP_LAVNX16_XP(xb_vecNx16 v_out, valign a_load /*inout*/, const xb_vecNx16 * src_ptr /*inout*/, int bytes_cnt);
在单次或连续一组 IVP_LAVNX16_XP 调用前需要调用一次:
valign a_load = IVP_LANX16_PP(src_ptr);
其中,a_load 存放的是起始地址为 [src_ptr & 0x40] 连续 64byte 的数据,a_load 的 64bytes 和 [src_ptr & 0x40 + 64] 地址处连续 load 的 64bytes 组成一个 128byte 的数组,以 [src_ptr | 0x40] 为偏移量从 128bytes 的数组中截取 bytes_cnt 个 bytes 输出到 v_out。注意 bytes_cnt 的值会被截断到 0~64 的合法范围,也意味着这个指令可以 cover 不足 64byte 的 load 操作,也就是所谓 tail_load。还有一个要说明的特点是,这个指令在 load 操作完成后会更新 src_ptr 和 a_load,src_ptr 的偏移量为 bytes_cnt 截断后的值,a_load 更新为 v_out 的内容,这两项更新使得该指令可以连续调用,而不用重新调用 IVP_LANX16_PP 和手动移动指针 src_ptr。
第二组:multiply、pack
Cadence DSP 上典型的计算流是 load 数据到 vector 中,施加计算指令,如果得到的中间结果的数值范围有升位的需求,就需要用位宽更大的 wide vector 来存,而后再通过 PACK 类指令将 wide vector 中的数据安全地压缩到 vector 的位宽表达范围内:
xb_vec2Nx24 IVP_MULUSP2N8XR16(xb_vec2Nx8U b, xb_vec2Nx8U c, xb_int32 d);
上面这条命令是两个类型为 xb_vec2Nx8U 的 vector 和两个 int16 捉对进行向量乘法,两个向量乘法的结果做一次向量加法,得到的输出是类型为 xb_vec2Nx24 的 wide vector。两组乘法分别是 b 和 d 的高 16 位之间进行,以及 c 和 d 的低 16 位之间进行。
xb_vec2Nx8U IVP_PACKVRU2NX24(xb_vec2Nx24 b, int c);
而这条 pack 指令就是可以将类型为 xb_vec2Nx24 的 wide vector 中每一个通道 24bit 的数据右移 c 位,接着饱和处理到 u8 的表达范围,得到的输出就是类型为 xb_vec2Nx8U 的 vector。
第三组:select
有时候我们的算法逻辑需要对两个 vector 进行 interleave 或者 deinterleave,下面这个指令就可以实现:
void IVP_DSELNX16I(xb_vecNx16 a, xb_vecNx16 b, xb_vecNx16 c, xb_vecNx16 d, immediate e);
该命令会将 d 中的 64byte 数据看成 64lanes * u8,c 中的 64byte 数据看成 64lanes * u8,然后先 d 后 c,从低位到高位,将 d 和 c 中的数据拼接成一个 128lanes * u8 数组。而 e 是一个立即数,e 的每一个不同取值都对应一个预置的 index_list,每一个 index_list 都是 0~127 整数序列的一个重排列。预置的 index_list 有 8bit/16bit 两种粒度的 interleave/deinterleave 操作,额外的,还支持各种 rotate_left/rotate_right 操作。
但是可能会遇到,IVP_DSEL2NX8I 中预置的若干种 index_list 均不能满足我们的需求,那就需要下面这个命令:
void IVP_DSELNX16(xb_vecNx16 a, xb_vecNx16 b, xb_vecNx16 c, xb_vecNx16 d, xb_vec2Nx8 e);
该命令将 d 和 c 中的数据按照先 d 后 c, 从低位到高位的顺序排成了一个 64lanes * 16bit 的数组,而 e 中数据就是 0~63 整数序的一个自定义序列。
第四组:gather/scatter
最后一组要介绍的指令就是高效的 gather/scatter。gather 是从一组不连续的 dram 地址中 load 数据存到一个 vector 里面,而 scatter 就是反向操作,将一个 vector 里面的数据 store 到离散的 dram 地址中去。想象中 gather/scatter 的指令开销应该非常大,但是实际应用中发现 gather/scatter 确实比一般的指令多花一些 cycle,但是 overhead 不明显,且有些场景不用 gather/scatter 的话 SIMD 就玩不转了,就只能用标量计算了。
简单解释一下 Cadence DSP 的 gather/scatter 效率高的原因。gather/scatter 指令不同于普通指令,gather/scatter 在触发 issue 之后是由 SuperGather 硬件模块全权接管。后者会将 dram 512bit 宽的 bank 进一步拆分成 8 个 64bit 宽的 sub-bank,并从硬件层面支持同时 load 分布在不同 sub_bank 的数据(当然这里存在更严重的 sub_bank_conflict 的风险,后文详细解释)。此外,gather 还被拆分成两个子命令,gathera 和 gatherd。gathera 才是 SuperGather 实际接管的指令,该指令负责收集离散地址上的数据到 gr 寄存器(gather register)。拆分指令的原因是 gathera 可以异步执行,不阻塞 DSP 的处理器继续执行其他指令。而 gatherd 是一条执行在 DSP 处理器上的指令,负责将 gr 寄存器里面收集完毕的数据拷贝到普通的 vector 寄存器,所以只有依赖 gatherd 返回值的命令才必须等待 gather 操作执行完毕。至于 scatter,除了 sub_bank 并发 store 的功劳,最关键的原因是 scatter 在遇到 sub_bank_conflict 的时候会做硬件层面的 buffer,等到有空闲 slot 的时候再调度 store 操作。
gather/scatter 的指令如下:
xb_gsr IVP_GATHERANX8U(const unsigned char * base_ptr, xb_vecNx16U offset_vec);
xb_vecNx16U IVP_GATHERDNX16(xb_gsr b);
void IVP_SCATTERNX16U(xb_vecNx16U out, const unsigned short * base_ptr, xb_vecNx16U offset_vec);
这里解释一下,IVP_GATHERANX8U 是 gather 32lanes * u8 的数据,然后每一个通道的 u8 数据高位补 0 拓展到 u16, 所以 gr 寄存器里面存的是 32lanes * u16 的数据。
性能优化
前文介绍了一些高频使用的 SIMD 指令,读者可以尝试开发自己的 DSP 算子了,但是第一版实现的性能可能不 ok,所以本节将补充一些优化算子性能的知识点。
理解 SWP
首先要介绍 Cadence DSP 的编译器进行优化调度的核心概念--SWP(software pipeline),不同于处理器执行指令时进行硬件层面的流水,SWP 是编译器对算子 inner loop 的不同 iter 的指令进行软件层面的流水,目的就是让 inner loop 编译后的 VLIW 中有效指令的密度更高,最小化 nop 的比例。
为了更直观的理解 SWP, 下面以 alphablend 为例,详细讲解一下编译器实际调度得到的 SWP:
#define _LOCAL_DRAM0_ __attribute__((section(".dram0.data"))) // 变量是分配在 dram0 上
#define _LOCAL_DRAM1_ __attribute__((section(".dram1.data"))) // 变量是分配在 dram1 上
#define ALIGN64 __attribute__((aligned(64))) // 变量在 dram 上的起始地址是 64byte 对齐的
#define WIDTH 256
#define HEIGHT 32
#define DATA_SIZE 8192 // 256 * 32 = 8192
uint8_t _LOCAL_DRAM0_ ALIGN64 src0[DATA_SIZE];
uint8_t _LOCAL_DRAM1_ ALIGN64 src1[DATA_SIZE];
uint8_t _LOCAL_DRAM1_ ALIGN64 dst[DATA_SIZE];
void alpha_blend(uint8_t* psrc0, uint8_t* psrc1, uint8_t* pdst, int16_t alpha) {
int32_t i, j, alpha_beta;
xb_vec2Nx8U* __restrict vpsrc0 = (xb_vec2Nx8U*) psrc0;
xb_vec2Nx8U* __restrict vpsrc1 = (xb_vec2Nx8U*) psrc1;
xb_vec2Nx8U* __restrict vpdst = (xb_vec2Nx8U*) pdst;
xb_vec2Nx8U vsrc0, vsrc1, vdst;
xb_vec2Nx24 wvec0;
alpha_beta = ((0x3fff - alpha) << 16) + alpha;
// DATA_SIZE = 256 * 32
// XCHAL_IVPN_SIMD_WIDTH = 32
for (i = 0; i < DATA_SIZE / 2 / XCHAL_IVPN_SIMD_WIDTH; ++i) {
vsrc0 = *vpsrc0++; // 因为这里 psrc0/psrc1 的地址是 64byte 对齐的,
// 所以汇编指令为 ivp_lv2nx8_ip vsrc0,vpsrc0,64
vsrc1 = *vpsrc1++;
wvec0 = IVP_MULUSP2N8XR16(vsrc1, vsrc0, alpha_beta);
vdst = IVP_PACKVRU2NX24(wvec0, 14);
*vpdst++ = vdst;
}
}
// call alpha_blend in main function
alpha_blend(src0, src1, dst, 8192);
上面的代码就是用 SIMD 写的一个 alpha_blend 算子,使用命令行工具拿到编译器调度后的汇编文件:
xt-xcc -S alphablend.c -o alphablend.s -O2
截取汇编文件中的 SWP 的部分如下:
#<loop> Loop body line 139, nesting depth: 1, kernel iterations: 62
#<loop> unrolled 2 times
#<swps>
#<swps> 4 cycles per pipeline stage in steady state with unroll=2
#<swps> 3 pipeline stages
#<swps> 10 real ops (excluding nop)
#<swps>
#<swps> 4 cycles lower bound required by resources
#<swps> min 3 cycles required by recurrences
#<swps> min 4 cycles required by resources/recurrence
#<swps> min 9 cycles required for critical path
#<swps> 12 cycles non-loop schedule length
#<swps> register file usage:
#<swps> 'a' total 4 out of 16 [2-4,10]
#<swps> 'v' total 6 out of 32 [0-5]
#<swps> 'wv' total 2 out of 4 [0-1]
#<swps> 'pr' total 1 out of 16 [0]
#<swps>
#<freq> BB:72 => BB:72 probability = 0.98438
#<freq> BB:72 => BB:79 probability = 0.01562
.frequency 1.000 63.492
// steady 阶段
{ # format N2
ivp_lv2nx8_ip v0,a2,128 # [0*II+0] id:45
ivp_lv2nx8_i v3,a2,64 # [0*II+0] id:45
}
{ # format N2
ivp_lv2nx8_ip v1,a3,128 # [0*II+1] id:46
ivp_lv2nx8_i v4,a3,64 # [0*II+1] id:46
}
{ # format F0
ivp_sv2nx8_ip v2,a4,128 # [2*II+2] id:47
ivp_packvru2nx24 v2,wv0,a10 # [1*II+2]
ivp_mulusp2n8xr16 wv0,v1,v0,pr0 # [0*II+2]
nop #
}
{ # format F0
ivp_sv2nx8_i v5,a4,-64 # [2*II+3] id:47
ivp_packvru2nx24 v5,wv1,a10 # [1*II+3]
ivp_mulusp2n8xr16 wv1,v4,v3,pr0 # [0*II+3]
nop #
}
从注释部分可以看出,编译器对循环体做了 unroll=2 的循环展开,展开后的 loop count 是 62,得到了一个 4cycle 3stage 的 SWP,并且告诉你该 SWP 中发射了 10 个非 nop 的指令(可以计算一下 CPI(cycle per instruction) 为 0.4),额外的还有一些寄存器占用比例的分析数据。
代码部分的每一个花括号就是一个 VLIW,注意每一个 VLIW 编码的指令数可以不一样,这是因为 Cadence DSP 支持了十余种不同 format 的 VLIW(代码中每个花括号上面都有一句注释表明了 format 类型)。然后每一句指令的右边都有一句注释,只需关注方括号的部分,加号右边的数字是表征当前指令在 SWP 的第几个 cycle 发射出去,加号左边与 II 相乘的数字表征的是 stage。因为 alphablend 调度出来的是一个 3stage 的 SWP,所以可以看到与 II 相乘的数字是 0,1,2,将其分别指代成 stage 0/1/2。这里 3 stage 的意思是,SWP 里会出现一个 VLIW 同时打包了三个 iter(unroll 之后的三个 iter)的指令,stage 0 是当前 iter, stage 1 是上一个 iter, stage 2 是上上一个 iter。
类比处理器硬件的 pipeline,上面这段代码准确说是 SWP 流水线填满的 steady 阶段,SWP 也有流水线填充和退出的阶段,分别称为 prologue 和 epilogue。这也解释了原始 loop 的 loop count 其实是 256 * 32 / 32 / 2 为 128,但是 SWP unroll 之后的 loop count 不是 64,而是 62。为了更直观的理解 SWP,下面将 prologue、steady 和 epilogue 三个阶段的汇编代码粘贴到一张图中,如下:
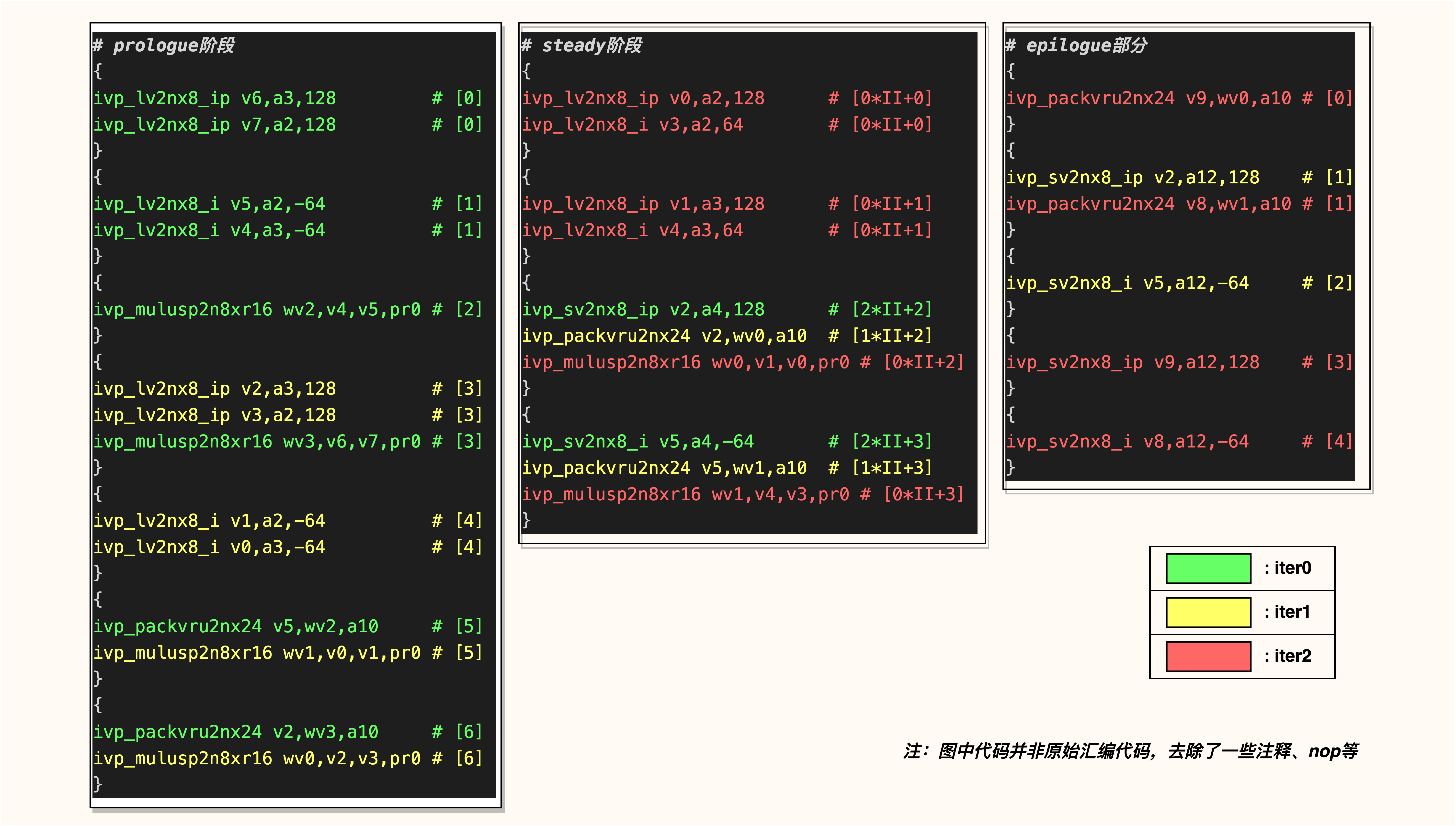
从图中可以看出,所谓的 SWP 就是将一个原始 iter 下不同的指令看成不同的 stage,并应用流水线的概念,把一个原始 iter 中有严格时序逻辑的多个指令的发射时机分散到 SWP 的不同 iter 中,目的就是追求更低的 CPI。
其实,我们还可以根据汇编代码估计算子的执行时间:steady 阶段 4cycle * 62 + prologue 阶段 7cycle + epilogue 阶段 5cycle = 260cycle,执行 xt-run 测得这个循环体的耗时是 276cycle,其他的 overhead 是 276-260=16cycle,所以根据汇编代码估算的计算时间已经很准了(但是也有例外,后文会提及)。
了解了 SWP 的概念,接下来我们对 alphablend 的实现做一些修改,观察对 SWP 的影响。第一个试验就是将修饰指针变量的__restrict 去掉,重新拿到汇编文件,SWP 现在长这样:
#<loop> Loop body line 143, nesting depth: 1, iterations: 128
#<swps>
#<swps> 8 cycles per pipeline stage in steady state with unroll=1
#<swps> 1 pipeline stages
#<swps> 5 real ops (excluding nop)
#<swps>
#<swps> 2 cycles lower bound required by resources
#<swps> min 8 cycles required by recurrences
#<swps> min 8 cycles required by resources/recurrence
#<swps> min 8 cycles required for critical path
#<swps> 8 cycles non-loop schedule length
#<swps> register file usage:
#<swps> 'a' total 4 out of 16 [2-4,11]
#<swps> 'v' total 2 out of 32 [0-1]
#<swps> 'wv' total 1 out of 4 [0]
#<swps> 'pr' total 1 out of 16 [0]
#<swps>
#<freq> BB:30 => BB:30 probability = 0.99219
#<freq> BB:30 => BB:32 probability = 0.00781
.frequency 1.000 127.992
{ # format N2
ivp_lv2nx8_ip v0,a2,64 # [0*II+0] id:49
ivp_lv2nx8_ip v1,a3,64 # [0*II+0] id:50
}
{ # format N1
nop #
ivp_mulusp2n8xr16 wv0,v1,v0,pr0 # [0*II+1]
}
{ # format N2
nop #
ivp_packvru2nx24 v0,wv0,a11 # [0*II+4]
}
{ # format N1
ivp_sv2nx8_ip v0,a4,64 # [0*II+7] id:51
nop #
}
可以看到新的 SWP 没有 unroll, 且 stage 为 1,这种情况表示编译器没有帮我们做 software pipeline,尽管还有这段 SWP 的注释代码,但是没有做任何有意义的调度。现在的 CPI=8/5=1.6,之前的版本 CPI 是 0.4, 所以性能下降了 3 倍多。当然这里速度差别这么大,还有一个原因是 inner loop 的逻辑太简单,不 unroll 的情况下编译器实在没有啥可调度的空间,无法发挥 VLIW 的优势。如果 inner loop 逻辑比较复杂,即使不 unroll,编译器通过 VLIW 也能提高指令的并行度,与 SWP 有效调度后的性能差距就不会如此明显。
这里解释一下,可能有读者看到 SWP 里面只有 4 个 VLIW,不清楚为啥要用 8 个 cycle。请注意看每条指令右侧方括号里面的注释,cycle 数确实是横跨了 0~7,而中间不连续的数字都会替换成相应个数的 bubble。为什么会产生 bubble? 是因为当前内循环的四条 VLIW,调度的是同一个 iter 的不同指令,相邻的 VLIW 的数据又都是写后读的依赖关系,所以连续发射出去之后,会存在前一个指令的结果还没有写回,后一个指令已经读取该数并来到 execute 阶段了,也就是所谓的 pipeline interlock。为了解决 interlock,就需要在前后两条 VLIW 之间加一定数量的 bubble。可能还会有细心的读者纠结为啥 vload 和 vmul 之间没有 bubble,这是因为笔者在 Q7 上跑的代码,而 Q7 对 dram 的 vload 延迟做了特殊优化。如果在 P6 上跑这个代码,就会看到 vload 和 vmul 之间也会有 bubble。
接着,我们针对 SWP 做第二个试验:地址非对齐访问。前面说过 src0/src1 都是 64byte 对齐的,所以看汇编代码会发现,vload 实际使用的是 ivp_lv2nx8_ip 指令。但是假设现在无法保证 src0/src1 是 64bytes 对齐的,就需要实现以下更通用版本的 alphablend:
void alpha_blend(uint8_t* psrc0, uint8_t* psrc1, uint8_t* pdst, int16_t alpha) {
// 注意,直接粗暴的把 64byte 对齐的地址都加了 1,构造非对齐地址
psrc0++;
psrc1++;
pdst++;
int32_t i, j, alpha_beta;
xb_vec2Nx8U* __restrict vpsrc0 = (xb_vec2Nx8U*) psrc0;
xb_vec2Nx8U* __restrict vpsrc1 = (xb_vec2Nx8U*) psrc1;
xb_vec2Nx8U* __restrict vpdst = (xb_vec2Nx8U*) pdst;
xb_vec2Nx8U vsrc0, vsrc1, vdst;
xb_vec2Nx24 wvec0;
alpha_beta = ((0x3fff - alpha) << 16) + alpha;
// DATA_SIZE = 256 * 32
// XCHAL_IVPN_SIMD_WIDTH = 32
valign va_dst = IVP_ZALIGN();
valign a_load1 = IVP_LA2NX8U_PP(vpsrc0);
valign a_load2 = IVP_LA2NX8U_PP(vpsrc1);
for (i = 0; i < DATA_SIZE / 2 / XCHAL_IVPN_SIMD_WIDTH; ++i) {
IVP_LAV2NX8U_XP(vsrc0, a_load1, vpsrc0, DATA_SIZE - 1 - i * 64);
IVP_LAV2NX8U_XP(vsrc1, a_load2, vpsrc1, DATA_SIZE - 1 - i * 64);
wvec0 = IVP_MULUSP2N8XR16(vsrc1, vsrc0, alpha_beta);
vdst = IVP_PACKVRU2NX24(wvec0, 14);
IVP_SAV2NX8U_XP(vdst, va_dst, vpdst, DATA_SIZE - 1 - i * 64);
}
IVP_SAV2NX8UPOS_FP(va_dst, vpdst);
}
使用 xt-run 测得内循环的耗时是 298cycle,略多于对齐地址版本的 276cycle,继续查看非对齐地址版本的 SWP(unroll 太多,篇幅原因只截取 SWP 头部的注释):
#<loop> Loop body line 112, nesting depth: 1, kernel iterations: 15
#<loop> unrolled 8 times
#<swps>
#<swps> 16 cycles per pipeline stage in steady state with unroll=8
#<swps> 2 pipeline stages
#<swps> 48 real ops (excluding nop)
#<swps>
#<swps> 14 cycles lower bound required by resources
#<swps> min 8 cycles required by recurrences
#<swps> min 14 cycles required by resources/recurrence
#<swps> min 15 cycles required for critical path
#<swps> 23 cycles non-loop schedule length
#<swps> register file usage:
#<swps> 'a' total 12 out of 16 [2-5,8-15]
#<swps> 'v' total 4 out of 32 [0-3]
#<swps> 'u' total 3 out of 4 [0-2]
#<swps> 'wv' total 2 out of 4 [0-1]
#<swps> 'pr' total 1 out of 16 [0]
#<swps>
#<freq> BB:83 => BB:83 probability = 0.93750
#<freq> BB:83 => BB:88 probability = 0.06250
发现编译器搜出来一个 unroll=8,CPI=16/48=0.33(比地址对齐版本的 0.4 更低一点)的 SWP,但是因为 unroll 太大,prologue/epilogue 的 CPI 比较大才导致总的 cycle 数略大于地址对齐版本。但是如果 loop_count 更大一点,两个版本的速度差异就更小了。不知道读者会不会失望了,这个试验的结果并没有告诉我们怎么做速度更快,只是得出一个结论:非地址对齐的算子速度不一定比地址对齐的版本要慢,但是非地址对齐版本的算子会更通用一点。
理解 bank_conflict
回过头来填一个坑,为什么基于汇编代码估算 DSP 时间有时候会不准?其实原因前文也有提过,就是 bank_conflict 和 sub_bank_confilct 搞的鬼。
先说 bank_conflict 的影响,还是拿前面的 alphablend 做例子。该算子有两个输入 src0/src1,如果有两条 vload 指令被调度到同一个 VLIW 里面,且访问的两个地址是同一个 dram 上同一个 bank 的不同位置,就触发了 bank_confilct,处理器必须 stall 一个 cycle。直觉告诉我们如果将 src0 和 src1 放在不同的 dram 上,应该会降低 bank_confilct 发生的概率。
做个试验验证下,把前面最初版本的 alphablend 的 src0/src1 都放到 dram0 上,测得内循环的耗时从原先的 276cycles 变成了 280cycles。速度下降好像并不明显,查看 SWP 没有发生任何变化,后面这点倒是符合预期,因为编译期并不会检查每一次地址访问有没有发生 bank_conflict。仔细看汇编代码可以发现,steady 阶段的代码都是同一个 dram 的连续两个 64byte 的 vload 被放在了一个 VLIW 里面,所以本次试验修改对其不产生影响。增加的 4 个 cycle 其实是因为 prologue 阶段有四个绑定了不同 dram 上 vload 指令的 VLIW,恰好这四个 VLIW 都触发了 bank_confilct。考虑到不同算子的调度情况是不一样的,为了减少 bank_conflict 对性能的影响,我们还是应该将多个输入 tile 创建在不同的 dram 上。
接着,我们来分析一下 sub_bank_conflcit 对性能的影响。sub_bank_conflict 只会发生在 gathera 指令的执行过程中,当 gathera 收集非连续地址上的多个数据时,如果出现多个数据的地址正好在同一个 dram 的同一个 bank 的同一个 sub_bank 中的不同地址时,就会出现多次 sub_bank_conflict,最极端的情况下收集一个 vector32,却出现了 32 次 conflcit,gathera 收集完成需要 32 个 cycle。
所以如果我们开发的算子里面用到了 gathera 指令,请加上-mem_model 选项在模拟器上跑一下,执行完会打印一些统计参数,其中一项就是 gather stall 的 cycle 数。如果不幸 gather stall 比较大,就需要检查算子里面的访存逻辑,看看是否需要调整 tile 上数据的分布情况,比如可以在 tile 的水平方向插入若干列的无用数据,降低 gathera 目标数据在同一个 sub_bank 的可能性。
性能优化小结
综上,从算子实现的维度上看,Cadence DSP 算子的速度只受限于 SWP 调度出来的 CPI,以及访存的 bank 冲突。
最后,将散落在本文各个地方会影响算子性能的点集中到一起(还有一些可以降低 CPI 的技巧前文没有提及),做成 checklist 便于大家对照查看:
-
确认算子频繁访问的数据是不是位于 dram 上?而不是 ddr 上。
-
确认是否使用了 pingpog dma,以及使用了之后是否真的隐藏了 dma 搬运的开销?可以检查 kernel 耗时占总耗时的比例。
-
确认 load/store 和 gather/scatter 访问的 dram 指针是否都加上了__restrict?
-
如果算子核心计算逻辑是两重 for 循环,确认是否将 tile_height 作为内层循环?以及是否将外层循环 unroll?
-
如果使用了 gather 指令,请查看 gather stall 的 cycle 数是否很高?然后对症下药。
-
确认算子内循环中使用的局部变量是否过多?如 filter2d 在 kernel_size 大于等于 5 的情况,为了避免寄存器溢出,需要将单一的内循环拆分成多个小的独立的内循环。
-
如果是 elemwise 类操作,计算逻辑比较复杂,但是每一个像素值最终的处理结果在一个比较有限的范围内,比如一些色彩处理类算子,输入是 u8 或 u8 的二元组,经过一系列处理逻辑,最后的结果还是 u8 或 u8 的二元组。这种情况下建议转换思路看看查表操作是否 ok(因为我们在 DSP 上有 SuperGather)。
-
如果算子有多个输入,确认有没有施加降低 bank_confilct 的措施?
9、如果从较早的 DSP 型号上移植算子到较新的 DSP 型号上,比如移植 P6 上的代码到 Q7,需要注意新指令的应用,比如 Q7 比 P6 多了 Dual-Quad 8x8 和 Quad 32x16 multiply 两个可选的增强模块。
杂项
本节整理了一些在前文不便展开的细节,但其实也很重要:
-
gathera 指令有很多变种,有些变种 gathera 指令的 offset_vec 是 16lanes * u32, 但是必须注意的是 offset_vec 里的数据必须是 0~65535 范围内。否则,SuperGather 会读取不到对应地址的数据,并给该 lanes 直接赋 0。
-
开发测试的过程中可能会有修改 memmap.xmm 文件的需求,比如调整栈空间的位置和大小,只需要编辑完 xmm 文件之后,使用 xtensa 命令行工具 xt-genldscripts,在 xmm 文件所在目录下执行
"xt-genldscripts -b ."命令,即可在。/ldscripts 目录下得到新的 linker scripts 文件,对 xmm 的修改也即生效。 -
举两个有可能发生高频 sub_bank_conflict 的例子:一个例子是 padding 算子在做 left_padding 和 right_padding 的时候,会 gather 一个 tile 的某一列连续若干个数据,如果恰好该列所有的数据都在同一个 sub_bank 就会性能非常差;还有一个例子就是 transpose,dst_tile 的一行其实是 src_tile 的一列,所以 gather 的时候同样有可能出现极端的 sub_bank_conflict。
-
解释一下编译器只对 inner loop 应用 SWP 调度优化的原因,Cadence DSP 的应用定位就是图形处理,而一般图形处理算法的 inner loop 计算密度非常高,几乎决定了整个算法的性能。
-
SWP 优化调度的 inner loop 实际上是号称 zero overhead loop 的,也就是说没有普通 loop 检查循环条件,更新 loop iter 等工作的开销,但是上面的 alphablend 的例子中好像 inner loop 还是有一些 overhead 的,是因为想要获取 zero overhead 的 inner loop,还需要两个额外条件:inner loop 里面指令数不能太少,且 loop count 相对较大。
-
前文提到将不同的输入 tile 存放在不同 dram 上来减少 bank_confilct,但是减少 bank_conflict 的终极策略是:先将不同的 tile 存放在不同的 dram 上,然后代码里使用
#pragma ymemory (tile_on_dram0)告诉编译器哪一个 tile 是在 dram1 上的,编译器会将该 tile 的内存类型标记为 ymemory,而其他 tile 的内存类型标记为 xmemory,最后增加一个编译选项-mcbox,告诉编译器只有访问不同内存类型的两个 vload 指令才可以打包到同一个 VLIW 里去。
总结
本文详细介绍了 Cadence DSP 的架构特点,算子的调用流程,算子的分块执行逻辑,以及算子的开发、调试和优化实践,希望可以给后面从事相关开发的同学起到一个抛砖引玉的作用。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号