CF1100G Tree-Tac-Toe 题解

这题在 CF rating 是 3100+，听了讲评之后感觉醍醐灌顶。

如果您不看题解就 AC，那您是真的强。

首先，我们发现，黑不可能赢。

接下来，考虑一种简单的情况：没有任何点初始时有颜色。

情况 1：树中有一个点 \(A\) 的度大于等于 \(4\)。

我们假设它连着 \(B,C,D,E\) 等点。那么，白方下 \(A\)，不妨令黑下在 \(B\)，白下 \(C\),此时白有两个未被阻挡且连起来的点，白胜。

剩下的情况中，每一个点的度都小于等于 \(3\)。

情况2：树中有一个点度为 \(3\) ，且从这个点伸出至少两个长度至少为 \(2\) 的链。

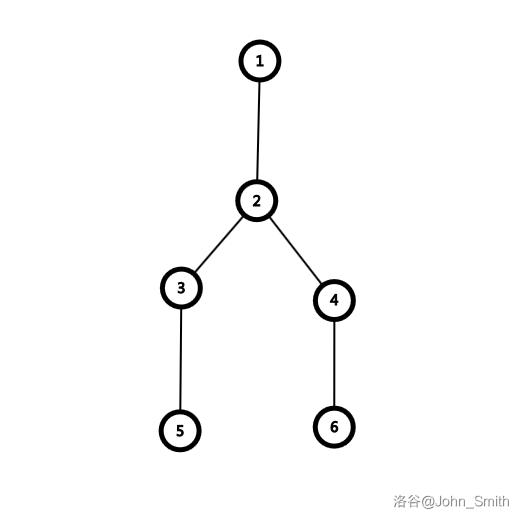
白下 \(2\)，不妨另黑下 \(3\)，则白下 \(4\)，此时白有两个未被阻挡且连起来的点，白胜。

剩下的情况中，每一个点最多伸出一条长度大于等于 \(2\) 的链，并且容易发现，此时至多有 \(3\) 个度为 \(3\) 的点。否则，可以放入情况 2 中。

此时任选其中的两个点做讨论。此时，它们会出现图示的 \(\text{H}\) 形结构。

一、两条竖杆中间夹着偶数个点。

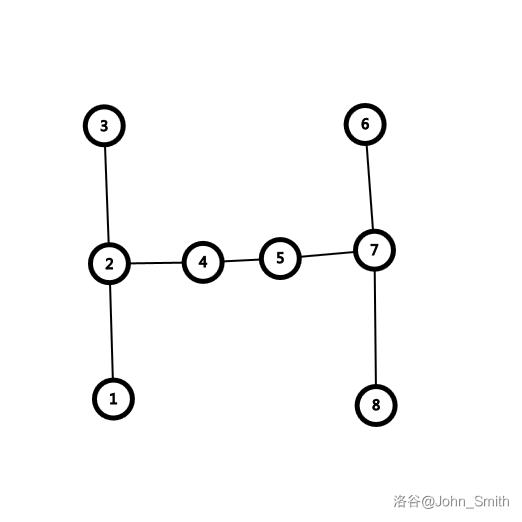
白下 \(4\)，黑只能下 \(2\)；白下 \(5\)，黑下 \(7\)，平。

二、两条竖杆之间夹着奇数个点。

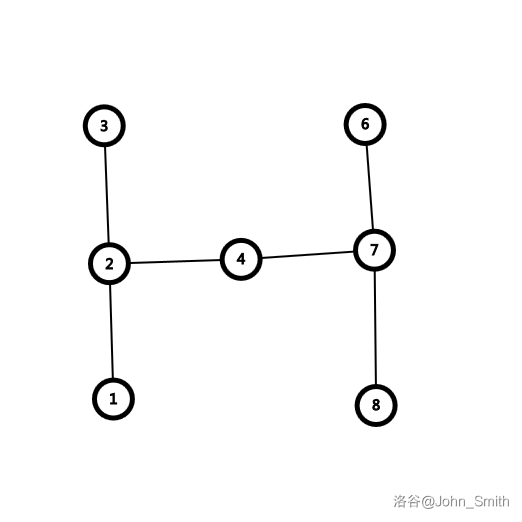
白下 \(4\)，不妨另黑下 \(2\)；白下 \(7\)，不管黑堵住哪一边，白都能走另外一边连成 \(3\) 个子。

我们转化为一般的情况。假设中间被夹着的点是 \(1\) 至 \(n\)。白最优解就是下 \(1\) 和 \(n\)，那么黑就会堵住另外两边的点（\(1\) 前面的，\(n\) 后面的）；然后白就会隔一个位置下一个子，然后黑为了防止白连成三个子，就会下在白中间的空位。就这样一直往中间下，如果最后白最中间的两个子有一个空位，则白胜（因为此时会留下两个空，无论黑占掉哪一个，白都可以下；另一个空而胜利）。

容易发现，上面这段等价于：\(n\) 为奇数则白胜，否则平。

剩下的情况就是一条链了。这是黑和白会一直纠缠，最终平。上面就是所有情况。

如果最开始有白色的点呢？我们使用化归的思想，把左侧的 \(A\) 转化为右侧的 \(A'\)：

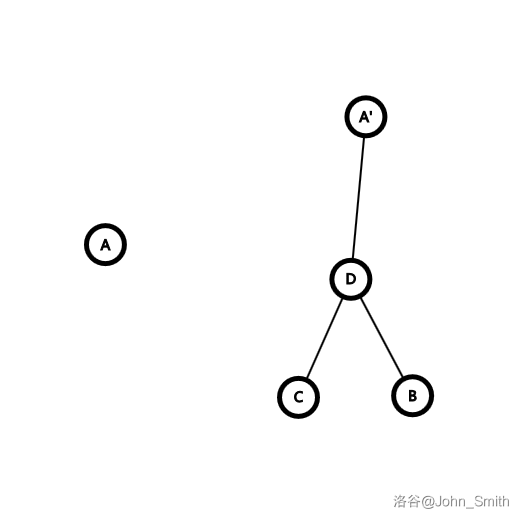
其中，右侧所有点未染色，且 \(B,C,D\) 是新添加的。

思考一下意义：如果 \(A'\) 此时被白下，黑为了不负必定下 \(D\)，此时 \(C,B\) 就被浪费掉了（如果在这里黑子想连成三个，由于白先下，那么黑也比白慢，必须与白牵制），相当于让白多下了。

没了。注意每次清零的时候别用 memset，直接循环赋 \(0\)，否则 T 飞第二个点。

代码：

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(register int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(register int i=(a);i>=(b);--i)
#define read() Read<int>()
#define write Write<int>
#define writesp Writesp<int>
#define writeln Writeln<int>
template<typename T>
inline T Read()
{
	bool f=0;T x=0;char ch;
	do{ch=getchar();f|=(ch=='-');}while(!isdigit(ch));
	do{x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}while(isdigit(ch));
	return f?-x:x;
}
template<typename T>
inline void Write(T x)
{
	if(x<0){putchar('-');write(-x);return;}
	if(x>9)write(x/10);
	putchar(x%10+48);
}
template<typename T> inline void Writeln(T x){Write(x);puts("");}
template<typename T> inline void Writesp(T x){Write(x);putchar(' ');}
const int maxn=2e6+5;
int nxt[maxn<<1|1],to[maxn<<1|1],head[maxn],tot=0;
int n;
void addedge(int u,int v)
{
	nxt[++tot]=head[u];
	head[u]=tot;
	to[tot]=v;
}
int deg[maxn];
bool judge1()//判断是否有度>=4的点 
{
	rep(i,1,n)if(deg[i]>3)return 1;
	return 0;
}
//接下来的情况中，所有点的度都<=3 
bool judge2()//判断是否有挂着两条长度>=2的链的点 
{
	rep(u,1,n)
	{
		int count=0;
		if(deg[u]!=3)continue;
		for(register int i=head[u];i;i=nxt[i])
		{
			int v=to[i];
			if(deg[v]>1)++count;
		}
		if(count>1)return 1;
	}
	return 0;
}
int dis[maxn];
void dfs(int u,int fa)
{
	dis[u]=dis[fa]+1;
	for(register int i=head[u];i;i=nxt[i])
	{
		int v=to[i];
		if(fa==v)continue;
		dfs(v,u);
	}
}
//接下来，每一个点只有可能挂着一条长链，剩下的地方都只连接着一个点
bool judge3()//判断“H”形情况
{
	int a=0,b=0,c=0;
	rep(i,1,n)
	{
		if(deg[i]>=3)
		{
			if(a&&b){c=i;break;}
			if(a){b=i;}
			else a=i;
		}
	}
	if(!b&&!c)return 0;
	memset(dis,0,sizeof dis);dfs(a,0);
	int len=dis[b];
	if(len&1)return 1;
	if(!c)return 0;
	len=dis[c];
	if(len&1)return 1;
	memset(dis,0,sizeof dis);dfs(b,0);
	len=dis[c];
	if(len&1)return 1;
	return 0;
} 
int main(){
	int t=read();
	while(t--)
	{
		n=read();
		rep(i,1,n-1)
		{
			int u=read(),v=read();
			addedge(u,v);
			addedge(v,u);
			++deg[u];++deg[v];
		}
		int cur=n;
		rep(i,1,n){
			char ch;cin>>ch;
			if(ch=='W')
			{
				cur+=3;
				addedge(i,cur-2);addedge(cur-2,i);
				addedge(cur-1,cur-2);addedge(cur-2,cur-1);
				addedge(cur,cur-2);addedge(cur-2,cur);
				deg[i]++;deg[cur-2]=3;
				deg[cur-1]=deg[cur]=1;
			}//拆点 
		}
		n=cur;
		if(judge1()){puts("White");}
		else if(judge2()){puts("White");}
		else if(judge3()){puts("White");}
		else puts("Draw");
		rep(i,1,n)deg[i]=head[i]=0;
		tot=0;
	}
	return 0;
}