求1-1000中能被3或5整除的数字之和

昨天在QQ群上看到一道题，“求1-1000中能被3或5整除的数字之和”

其中看到很有趣的解法二，最开始还是挺迷惑的， 后来想了下，再经人指点，就觉得茅塞顿开。

第一种解法很普遍，就是将1000以内的数都遍历一遍，只要有整除3或者整除5的数，就将其加起来，最终得到一个总的和。

让我感兴趣的是第二种解法，这里巧妙运用了数学上的等差数列

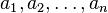一个公差为d的等差数列a_1,a_2,\dots,a_n前n项的级数为：

S_n = a_1+a_2+\dots+a_n=\sum_{i=0}^{n-1} (a_1+id)=\frac{n( a_1 + a_n)}{2} =\frac{n[ 2a_1 + (n-1)d ]}{2}.
第二种方法第一步就用了(a1+an)/3*3,所以就变成了3*（1+333）*333/2，这一步就是把整除3的所有项都加起来。
同理，sum(Math.floor(input-1)/5))*5中，就把1000以内中能整除5的所有项都加起来
最后能整除3和整除5里面有重复的数，比如15，这时就把重复除以15的数减掉，就能获得1000以内能被3或5整除的数字之和。
posted @ 2016-02-18 15:17  janna~  阅读(4707)  评论(0)  编辑  收藏  举报