CCF CSP 201709-4 通信网络

CCF计算机职业资格认证考试题解系列文章为meelo原创，请务必以链接形式注明本文地址

CCF CSP 201709-4 通信网络

问题描述

　　某国的军队由N个部门组成，为了提高安全性，部门之间建立了M条通路，每条通路只能单向传递信息，即一条从部门a到部门b的通路只能由a向b传递信息。信息可以通过中转的方式进行传递，即如果a能将信息传递到b，b又能将信息传递到c，则a能将信息传递到c。一条信息可能通过多次中转最终到达目的地。
　　由于保密工作做得很好，并不是所有部门之间都互相知道彼此的存在。只有当两个部门之间可以直接或间接传递信息时，他们才彼此知道对方的存在。部门之间不会把自己知道哪些部门告诉其他部门。

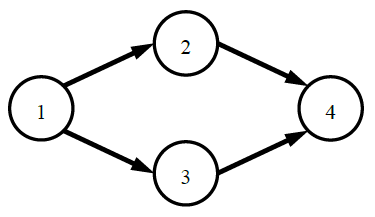
　　上图中给了一个4个部门的例子，图中的单向边表示通路。部门1可以将消息发送给所有部门，部门4可以接收所有部门的消息，所以部门1和部门4知道所有其他部门的存在。部门2和部门3之间没有任何方式可以发送消息，所以部门2和部门3互相不知道彼此的存在。
　　现在请问，有多少个部门知道所有N个部门的存在。或者说，有多少个部门所知道的部门数量（包括自己）正好是N。

输入格式

　　输入的第一行包含两个整数N, M，分别表示部门的数量和单向通路的数量。所有部门从1到N标号。
　　接下来M行，每行两个整数a, b，表示部门a到部门b有一条单向通路。

输出格式

　　输出一行，包含一个整数，表示答案。

样例输入

4 4
1 2
1 3
2 4
3 4

样例输出

2

样例说明

　　部门1和部门4知道所有其他部门的存在。

评测用例规模与约定

　　对于30%的评测用例，1 ≤ N ≤ 10，1 ≤ M ≤ 20；
　　对于60%的评测用例，1 ≤ N ≤ 100，1 ≤ M ≤ 1000；
　　对于100%的评测用例，1 ≤ N ≤ 1000，1 ≤ M ≤ 10000。

解析

如果图无环，计算每一个顶点父节点的个数及子节点的个数，如果二者之和加一等于总节点的个数，那么就是所求解的知道N个节点存在的节点。

统计一个节点父节点的个数可以通过N个深度优先搜索得到。从每一个节点开始进行深度优先搜索，每到达一个节点，该节点的计数加一。复杂度为O(V(V+E))

将图的所有边反向，便可以统计一个节点子节点的个数。

如果图存在环，在同一个强连通分量内的节点互相为父子节点，上面的方法便失效了。解决方案是首先进行强连通分量的分解。代码中使用了Kosaraju算法进行强连通分量的分解。复杂度为O(V+E)

分解后得到每一个顶点的强连通分量标号。

然后计算每一个节点父强连通分量的个数与子强连通分量的个数。这一步从每一个强连通分量中选择一个顶点开始进行深度优先搜索，如果当前所在强连通分量的标签与起始节点强连通分量标签不同，则该节点计数加一。

如果一个顶点父强连通分量的个数加上子强连通分量的个数加一等于总强连通分量个数，那么这个节点知道所有节点的存在。

代码

C++

#include <iostream>
#include <vector>
#include <algorithm>
#define MAX_V 1001
using namespace std;

int N, M;
vector<int> G[MAX_V], rG[MAX_V];
vector<int> postorder;
bool used[MAX_V];
int label[MAX_V]; // 每一个节点所属强连通分量的标号
int sccv[MAX_V]; // 每一个强连通分量的一个顶点
int nparent[MAX_V], nchild[MAX_V];  // 每一个节点父/子强连通分量个数 

// 生成图的后序遍历 
void dfs(int u) {
    for(int i=0; i<G[u].size(); i++) {
        int v = G[u][i];
        if(!used[v]) {
            used[v] = true;
            dfs(v);
        }
    }
    postorder.push_back(u);
}

int rdfs(int u, int l) {
    label[u] = l;
    for(int i=0; i<rG[u].size(); i++) {
        int v = rG[u][i];
        if(!used[v]) {
            used[v] = true;
            rdfs(v, l);
        }
    }
}

// Kosaraju算法 分解强连通分量 
int SCC() {
    fill(used, used+MAX_V, 0);
    for(int n=1; n<=N; n++) {
        if(!used[n]) {
            used[n] = true;
            dfs(n);
        }
    }
    fill(used, used+MAX_V, 0);
    int l = 0;
    for(int n=N-1; n>=0; n--) {
        int v = postorder[n];
        if(!used[v]) {
            l++;
            used[v] = true;
            rdfs(v, l);
            sccv[l] = v;
        }
    }
    return l;
}

// 统计u所在强连通分量能够到达的其它强连通分量 
void dfs2(int u, int l, int (&nparent)[MAX_V], vector<int> (&G)[MAX_V]) {
    if(label[u] != l) nparent[u]++;
    for(int i=0; i<G[u].size(); i++) {
        int v = G[u][i];
        if(!used[v]) {
            used[v] = true;
            dfs2(v, l, nparent, G);
        }
    }
}

int main() {
    cin >> N >> M;
    for(int m=0; m<M; m++) {
        int a, b;
        cin >> a >> b;
        G[a].push_back(b);
        rG[b].push_back(a);
    }
    
    int numc = SCC();
    
    // 统计每一个顶点父强连通分量个数 
    for(int i=1; i<=numc; i++) {
        fill(used, used+MAX_V, 0);
        int v = sccv[i];
        used[v] = true;
        dfs2(v, label[v], nparent, G);
    }
    
    // 统计每一个顶点子强连通分量个数 
    for(int i=1; i<=numc; i++) {
        fill(used, used+MAX_V, 0);
        int v = sccv[i];
        used[v] = true;
        dfs2(v, label[v], nchild, rG);
    }
    
    int cnt = 0;
    for(int n=1; n<=N; n++) {
        // 如果父强连通分量个数加子强连通分量个数加一等于总强连通分量个数 
        if(nparent[n]+nchild[n]+1==numc) cnt++;
    }
    cout << cnt;
}