阅读笔记：Merak 大模型并行训练系统
论文简介
Merak: An Efficient Distributed DNN Training Framework With Automated 3D Parallelism for Giant Foundation Models 这篇论文发表在IEEE TPDS 2023上，主题是提出一种高效的具有三维并行性的自动化分布式训练系统-Merak。
论文背景和Motivation
3维并行训练即将数据并行（DP）、张量模型并行（TMP）和流水线模型并行（PMP）集成到多节点分布式训练系统的训练方式。DP和PMP是常用的分布式训练方法，例如DP以参数服务器模式和AllReduce模式为两种主要范式，而PMP也以GPipe和PipeDream为代表性工作。TMP则是由Megatron LM引入基于transformer的模型，即沿着行或列维度划分权重矩阵到不同的训练节点，并添加AllReduce操作以确保操作逻辑正确性。它在（前向传播）FP和（反向传播）BP过程中都会带来大量通信阻塞，这大大减缓了训练阶段的速度。
激活的重新计算：在模型训练过程中，中间的激活变量（activation）需要在反向传播的时候被重新计算，这是一种在大模型训练的情况下内存和计算权衡的结果，这种方法要多花大约1/3的运算开销来降低内存成本。
最新（SOTA）模型训练系统的缺点：
- 缺乏通用性：需要有经验的开发人员，手动设置模块或其他代码修改
- 低效率：PMP给GPU资源带来了气泡时间（bubble），TMP给张量计算引入了通信时间，因此带宽和计算资源都是低效率的
Merak旨在建立一个系统达到以下目标：
1）通过改进训练方式（DP，PMP，TMP）的整合来加速训练过程。
2）无需修改原始模型即可实现三维并行训练。
下图也说明了Merak在自动训练上的优势：
论文方法
系统的整体架构如下：
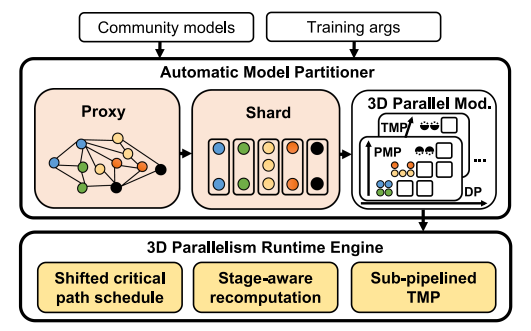
Automatic Model Partitioner
Proxy Nodes Graph
Merak是一个基于Pyotch的系统，所以为了模型分割，首先需要做的就是获得完整的计算图，这里Merak使用了torch.tx。但是在大模型场景下，torch.tx直接运行一次训练来获取计算图的思路并不可靠，显存容易溢出。所以Merak提出了一个代理节点图（Proxy Nodes Graph）的概念。
Merak设计代理节点来替代密集计算的计算图节点。代理节点不与任何参数相关联，也不执行计算，但它们可以根据输入返回适当大小的结果，从而正常参与计算图的跟踪确定。代理节点不需要计算的特点允许大模型在CPU中执行一步的推理。
这些代理计算图节点都是对一些特定的运算操作预设的，例如矩阵计算，注意力计算等。
Graph-Sharding Algorithm and Automated PMP
获得了模型的结构（计算图）之后，接下来就是设计一种模型水平划分算法来实时流水线并行（PMP）的模型分割操作。Merak使用的是一种启发式算法，算法原则：子图之间连接的节点数量应该是最小的（为了减少子图间的传输数据量）。因此，将不同的图划分为具有有限连接的顺序子图是其自动PMP划分的基本问题。
接下来，Merak提出了一个引理：一个节点应该保持在具有最远依赖关系的同一个子图中。同时，如果一个节点没有依赖关系，或者其最远的依赖关系是最新创建的子图，则可以将其放置到新的子图中。这个引理保证了前面提到的子图间的连接节点最小。
但是这种启发式的原则太严格，有些例如Mask Attention计算操作就被所有的注意力层引用为输入。所以Merak将一种节点定义为公共节点（commen node），并允许它们成为依赖的例外，以避免所有子图使用。
这里Merak论文提供了两个启发式规则算法。第一个是给定一个计算节点，返回其最远的依赖节点（需要该节点计算完成才能开始计算）的子图索引。第二个是给定一个计算图，返回最佳的子图分割。后者的核心是保证所有的节点和它的依赖节点位于同一个子图中，且当节点依赖为1或者子图超过了显存限制时创建新的子图。
Hign-Performance Training
Shifted Critical Path Schedule
这里论文提出的关键路径下移方法比较暧昧，关键路径（Critical Path）就是整个工作流中时间最长的一条路径，也是最终直接影响流水线计算图的路径。下图给出了几种流水线并行的计算时间图：
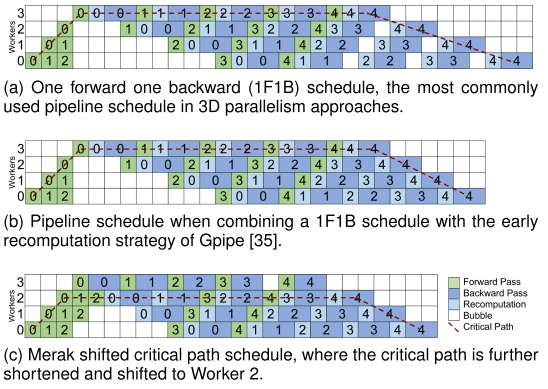
上图中(a)即一般的训练方法，其中每个mini-batch都需要等待前一个mini-batch的训练反向传播完成，所以虽然可以流水并行，但后期还是出现了气泡时间。 (b)则是GPipe的训练方法，GPipe划分mini-batch为micro-batch，彼此之间不需要等待参数更新，可以认为训练是独立的，所以减少了后期流水的气泡时间。 (c)是Merak的计算时间图，Merak的关键路径迁移方法即避免最后一个子图（stage）的激活重计算，因为最后一个子图并不需要等待任何节点就可以直接反向传播，所以直接使用前向计算得到的激活即可。
所以这里突出的关键路径下移的的方法就是避免最后子图的重计算。
这种方法被很多论文都提到了，似乎这里是改名重提？
Stage-Aware Recomputation
前面已知激活重计算是一种显存和计算时间的权衡，这里的主题就是根据子图（stage）来判断是否应该重计算激活或者重计算多少的激活。
首先给出数学上的推导，定义\(m\)为micro-batch的数量，\(s\)为子图总数，\(M_r\)为进行前向计算和反向传播在不保存激活时的显存占用大小，\(M_a\)为一个micro-batch里一个激活的大小。当第\(i\)级的子图节点上有\(a_i\)个模块不使用激活重新计算时，它们需要额外的内存占用\((s−i)\alpha_i M_a\)。这里的\(s-i\)来自于流水线图中前面的节点需要多保存一些micro-batch的激活。
优化目标为最大化显存的利用率，为此论文做出了一个假设（似乎没有合理性证明）：假设在最佳情况下，每个子图的设备都有相同的显存消耗，并且每个设备都已满载。基于这个假设，论文推导在i和j级子图节点的最佳重计算比例满足：
由此，可以推导出一个迭代计算公式来更新所有的\(a_i\)，如下：
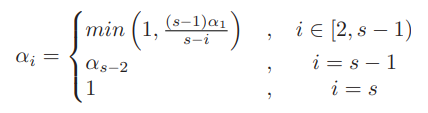
其中的\(a_1\)是对第一个子图从1开始逐渐增加，直到保存的激活总量超过了内存限制为止得到的。
Sub-Pipelined TMP
在子流水线TMP中，Merak将TMP块的每个micro-batch均匀地划分为两个sub-micro-batch，它们的训练过程是相互独立的，这样可以在计算和通信交替的资源间隙中填充空闲时间，如图所示：
实验
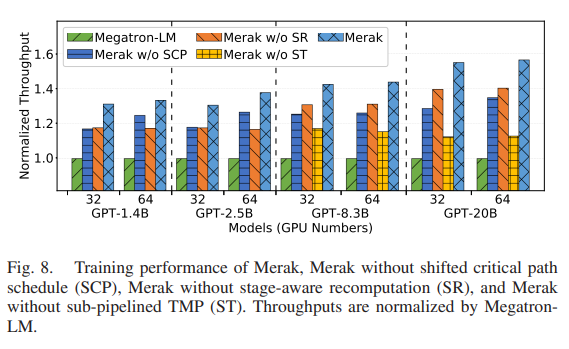
基本实验部分都齐全，例如总体表现，模块表现等等，并且使用的都是GPT结构模型。这里列出来一个实验结果：
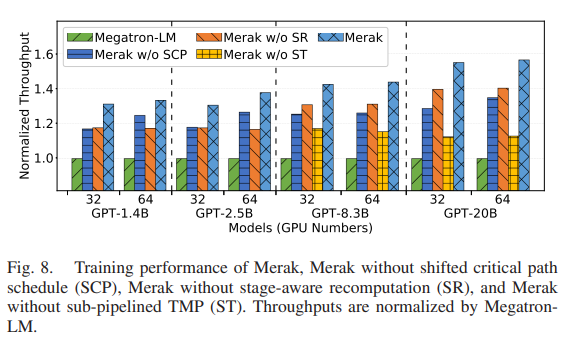
如图所示，在GPU节点较少的时候关键路径下移的效果略好于子图重计算规划，随着GPU数量的增加，效果逐渐反过来了。
讨论
子图重计算的推导，假设资源使用全部一致为最优情况以及几个统一的（无视子图结构）变量\(M_a, M_r\)是否合理？
