记忆化搜索

 滑雪   POJ - 1088 

Glory非常喜欢玩滑滑梯游戏，下面给出了一个n,m的滑道，其中的数字表示滑道的高度。Glory可以从一个点出发向下滑行，每次只能滑行到相邻的位置(上下左右)中高度严格低于当前高度的地方，不能重复划行已经滑行过的地方，但他希望在这个滑道上滑行尽量远的距离，也即是找一条最长的滑道。

Input

第一行输入两个数n,m代表滑梯范围行n和列m(1 <= n,m <= 100)。下面是n行，每行有m个整数，代表高度h，(0<=h<=20000)

Output

输出一个值，代表Glory能够在滑滑梯上面滑行的最长长度是多少

Sample Input

3 3
9 1 2
5 6 7
8 4 3

Sample Output

4

Sample Input

4 7
7 6 5 4 3 2 1
1 5 1 1 1 1 1
1 4 3 1 1 1 1
1 5 6 7 8 1 1

Sample Output

7

hint

样例1：7->6->4->3 长度为4

解题思路:

使用dfs得出最大值，记忆化搜索。用的无返回值的dfs。

代码： 

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <cmath>
using namespace std;
const int N=110;
int arr[N][N];
int vis[N][N];
int dp[N][N];
int dx[4]={0,0,-1,1};
int dy[4]={1,-1,0,0};
int sum=0,ans=0,n,m;
void dfs(int x,int y,int h){
    if(dp[x][y]){//如果这个点已经来过，直接得出最大sum与ans比较大小 
        sum+=dp[x][y];
        ans=max(ans,sum);//加多少减多少 
        sum-=dp[x][y];
        return ;
    }
    ans=max(ans,sum);//取最大的 
    int xx,yy;
    for(int i=0;i<4;i++){
        xx=x+dx[i];
        yy=y+dy[i];
        if(xx>0&&yy>0&&xx<=n&&yy<=m&&arr[xx][yy]<h&&vis[xx][yy]==0){
            vis[xx][yy]=1;
            sum++;
            dfs(xx,yy,arr[xx][yy]);// 继续下一个点 
            sum--;
            vis[xx][yy]=0;
        }
    }
    return ;
}
int main(){
    int res=0;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>arr[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            memset(vis,0,sizeof(vis));
            sum=0;
            ans=0;
            dfs(i,j,arr[i][j]);//找这个点能划的最长距离 
            res=max(ans,res);//记录最大值 
            dp[i][j]=ans; //记录 
        }
    }
    cout<<res+1<<endl;
    
    return 0;
}
 

 

FatMouse and Cheese  （hdu-1078）

有一种游戏是的玩法是这样的：
有一个n*n的格子,每个格子有一个数字。
遵循以下规则:
1. 玩家每次可以由所在格子向上下左右四个方向进行直线移动，每次移动的距离不得超过m
2. 玩家一开始在第一行第一列，并且已经获得该格子的分值
3. 玩家获得每一次移动到的格子的分值
4. 玩家下一次移动到达的格子的分值要比当前玩家所在的格子的分值要大。
5. 游戏所有数字加起来也不大，保证所有数字的和不会超过int型整数的范围
6. 玩家仅能在n*n的格子内移动，超出格子边界属于非法操作
7. 当玩家不能再次移动时，游戏结束
现在问你，玩家所能获得的最大得分是多少？

Input

有多组测试数据
每组测试样例第一行是两个整数n,m (1≤n≤100)(1≤m≤100),当n和m都是-1时为程序结束标志，直接退出即可
之后n行，每行n个数字，描述n*n的格子里的数字

Output

对于每组测试数据输出一行，这一行仅有一个整数，代表玩家所能获得的最高得分 

Sample Input

3 1

1 2 5

10 11 6

12 12 7

-1 -1

Sample Output

37

解题思路：

直接找最大距离，数据量过大，所以需要用记忆化数组，使用带返回参数的dfs，用dp记录dfs中每个点返回的从该点能到达的最远距离。

代码：

#include <bits/stdc++.h>
using namespace std;
int dp[110][110];
int vis[110][110];
int arr[110][110];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int n,m;
int dfs(int x,int y){
    if(dp[x][y])    return dp[x][y];//如果计算过则直接得出 
    int xx,yy;
    for(int i=0;i<4;i++){
        for(int j=1;j<=m;j++){
            xx=x+dx[i]*j;
            yy=y+dy[i]*j;
            if(xx>0&&yy>0&&xx<=n&&yy<=n&&arr[xx][yy]>arr[x][y]&&vis[xx][yy]==0){
                vis[xx][yy]=1;
                dp[x][y]=max(dp[x][y],dfs(xx,yy)+arr[x][y] );//去从四个方向中的最大值 
                vis[xx][yy]=0;
            }
        }
    }
    return dp[x][y]=max(dp[x][y],arr[x][y]);//返回该点能走的最大距离 
}

int main(){
    while(cin>>n>>m&&n!=-1){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                cin>>arr[i][j];
            }
        }
        memset(dp,0,sizeof(dp));//初始化 
        memset(vis,0,sizeof(vis));
        vis[1][1]=1;
        cout<<dfs(1,1)<<endl;    
    }
    
    
    
    return 0;
}

 

漫步校园   （hdu-1428）

Problem Description

LL最近沉迷于AC不能自拔，每天寝室、机房两点一线。由于长时间坐在电脑边，缺乏运动。他决定充分利用每次从寝室到机房的时间，在校园里散散步。整个HDU校园呈方形布局，可划分为n*n个小方格，代表各个区域。例如LL居住的18号宿舍位于校园的西北角，即方格(1,1)代表的地方，而机房所在的第三实验楼处于东南端的(n,n)。因有多条路线可以选择，LL希望每次的散步路线都不一样。另外，他考虑从A区域到B区域仅当存在一条从B到机房的路线比任何一条从A到机房的路线更近(否则可能永远都到不了机房了…)。现在他想知道的是，所有满足要求的路线一共有多少条。你能告诉他吗?

Input

每组测试数据的第一行为n(2=<n<=50)，接下来的n行每行有n个数，代表经过每个区域所花的时间t(0<t<=50)(由于寝室与机房均在三楼，故起点与终点也得费时)。

Output

针对每组测试数据，输出总的路线数(小于2^63)。

Sample Input

3

1 2 3

1 2 3

1 2 3

3

1 1 1

1 1 1

1 1 1

Sample Output

1

6

解题思路：

题意不太还理解，但不是本题重点。本题先要用bfs求出终点到各个点的最短距离，然后在用dfs求出可行的数目。

代码：

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long ll;
const int N=55;
const int MAX=1e5;
int arr[N][N];
int ans[N][N];
int vis[N][N];
ll dp[N][N];
int dx[4]={0,0,-1,1};
int dy[4]={1,-1,0,0};
int n;
ll res=0;
struct aa{
    int x,y,d;
    friend bool operator<(const aa &x,const aa &y){
        return x.d>y.d;
    }
};
int bfs(int x,int y,int d){//想用bfs求得从终点到各个点的最短距离。 
    priority_queue<aa>que;//因为在每个地方用的时间不同，所以需要用优先队列。 
    que.push({x,y,d});
    ans[x][y]=d;
    vis[x][y]=1;
    int xx,yy;
    while(que.size()){
        x=que.top().x;
        y=que.top().y;
        d=que.top().d;
        que.pop();
        for(int i=0;i<4;i++){
            xx=x+dx[i];
            yy=y+dy[i];
            if(xx>0&&yy>0&&xx<=n&&yy<=n&&vis[xx][yy]==0){
                vis[xx][yy]=1;
                ans[xx][yy]=arr[xx][yy]+d;
                que.push({xx,yy,d+arr[xx][yy]});
            }
        }    
    }
    return 0;
}
ll dfs(int x,int y){//dfs来求方法数目,dfs的返回值是方法数目，因为是记忆化搜索，不能直接用一个sum记录，每个函数都带个返回值。 
    if(dp[x][y]) return dp[x][y];
    int xx,yy;
    for(int i=0;i<4;i++){
        xx=x+dx[i];
        yy=y+dy[i];
        if(xx>0&&yy>0&&xx<=n&&yy<=n&&ans[xx][yy]<ans[x][y]&&vis[xx][yy]==0){
            vis[xx][yy]=1;
            dp[x][y]+=dfs(xx,yy);
            vis[xx][yy]=0;
        }
    }
    return dp[x][y];
}

int main(){
    while(cin>>n){
        res=0;
        memset(vis,0,sizeof(vis));
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                scanf("%d",&arr[i][j]);
            }
        }
        bfs(n,n,arr[n][n]);
        memset(vis,0,sizeof(vis));
        memset(dp,0,sizeof(dp));
        dp[n][n]=1;//另初始为1. 
        vis[1][1]=1;//标记 
        cout<<dfs(1,1)<<endl;
    }
    
    
    return 0;
}

 

Zipper  （hdu-1501）

Problem Description

Given three strings, you are to determine whether the third string can be formed by combining the characters in the first two strings. The first two strings can be mixed arbitrarily, but each must stay in its original order.

For example, consider forming "tcraete" from "cat" and "tree":

String A: cat
String B: tree
String C: tcraete
As you can see, we can form the third string by alternating characters from the two strings. As a second example, consider forming "catrtee" from "cat" and "tree":
String A: cat
String B: tree
String C: catrtee
Finally, notice that it is impossible to form "cttaree" from "cat" and "tree". 

Input

The first line of input contains a single positive integer from 1 through 1000. It represents the number of data sets to follow. The processing for each data set is identical. The data sets appear on the following lines, one data set per line.

For each data set, the line of input consists of three strings, separated by a single space. All strings are composed of upper and lower case letters only. The length of the third string is always the sum of the lengths of the first two strings. The first two strings will have lengths between 1 and 200 characters, inclusive.

Output

For each data set, print:
Data set n: yes
if the third string can be formed from the first two, or
Data set n: no
if it cannot. Of course n should be replaced by the data set number. See the sample output below for an example.

Sample Input

3

cat tree tcraete

cat tree catrtee

cat tree cttaree

Sample Output

Data set 1: yes

Data set 2: yes

Data set 3: no

本题大意为：

给你三串字符串，你能用前两个组成第三个么，组成时每个字符串按顺序取出。

解题思路：

用两个坐标记录两个字符串取到字符的位置，然后用dp数组记录。用dfs来进行判断，看是否能行，能行就返回2。

Ac代码：

#include <bits/stdc++.h>
using namespace std;
int dp[220][220];
char s1[220],s2[220],s3[520];
int str(int a,int b,int c){
    if(dp[a][b])//如果这个点已经算出来了直接返回。 
        return dp[a][b];
    if(s3[c]=='\0'&&s1[a]=='\0'&&s2[b]=='\0') {//代表能组成，返回2 
        return dp[a][b]=2;
    } 
    char c1=s1[a],c2=s2[b],c3=s3[c];//逐一判断 
    if(c1==c3&&c2==c3){
        return dp[a][b]=max(str(a+1,b,c+1),str(a,b+1,c+1));//如果有一个可行就会返回2。 
    }
    else if(c1==c3){
        return dp[a][b]=str(a+1,b,c+1);
    }
    else if(c2==c3){
        return dp[a][b]=str(a,b+1,c+1);
    }
    else 
        return dp[a][b]=1; //都不满足代表不行，返回1. 
}

int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        memset(dp,0,sizeof(dp));
        scanf("%s %s %s",&s1,&s2,&s3);
        if(str(0,0,0)==2){//判断即可 
            printf("Data set %d: yes\n",i);
        }
        else{
            printf("Data set %d: no\n",i);
        }
    }
    return 0;
}

 

Free Candies （UVA - 10118 ）

                                   

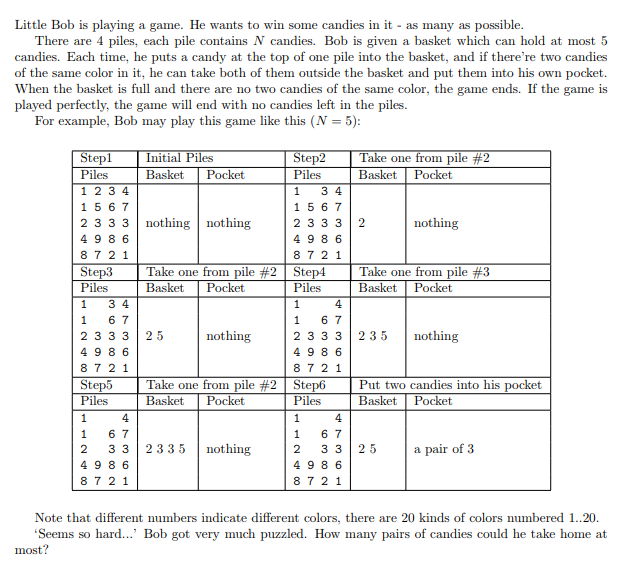
Input

The input will contain no more than 10 test cases. Each test case begins with a line containing a single integer n(1<=n<=40) representing the height of the piles. In the following n lines, each line contains four integers xi1,xi2,xi3,xi4 (in the range 1..20). Each integer indicates the color of the corresponding candy. The test case containing n=0 will terminate the input, you should not give an answer to this case.

Output

Output the number of pairs of candies that the cleverest little child can take home. Print your answer in a single line for each test case.

Sample Input

5

1 2 3 4

1 5 6 7

2 3 3 3

4 9 8 6

8 7 2 1

1

1 2 3 4

3

1 2 3 4

5 6 7 8

1 2 3 4

0

Sample Output

8

0

3

题目大意：

有4堆糖果，每堆有n（最多40）个，有一个篮子，最多装5个糖果，我们每次只能从某一堆糖果里拿出一个糖果，如果篮子里有两个相同的糖果，那么就可以把这两个（一对）糖果放进自己的口袋里，问最多能拿走多少对糖果。糖果种类最多20种.

解题思路：

利用记忆化搜索将搜有情况搜一遍，已经搜过的直接返回，统计对数最多的就行了。

ac代码：

#include <bits/stdc++.h>
using namespace std;
const int N=50;
int dp[50][50][50][50];//记忆化数组 
int p[N][5];//记录数据 
int n,ans=0,res=0;
int top[4];//代表的是已经取了第几堆的第几个了。 
int dfs(int count,int book[]){
    if(dp[top[0]][top[1]][top[2]][top[3]]){
        return dp[top[0]][top[1]][top[2]][top[3]];
    }
    if(count==5){//装满5个了，没法再装了返回。 
        res=max(ans,res);
        return dp[top[0]][top[1]][top[2]][top[3]]=ans;
    }
    for(int i=0;i<4;i++){
        top[i]++;
        if(top[i]>n) {//保证在该数组内。 
                top[i]--;
                continue;
            }
        if(book[p[top[i]][i+1]]==1){//包里有两个相同的了，减点两个放到口袋，对数加1，此种颜色数目变为0 
            book[p[top[i]][i+1]]=0;
            ans++;
            dfs(count-1,book);
            ans--;
            book[p[top[i]][i+1]]=1;
        }
        else{//包里没有相同的，包中数目加1 
            book[p[top[i]][i+1]]=1;
            dfs(count+1,book);
            book[p[top[i]][i+1]]=0;
        }
        top[i]--;//回溯 
    }
    res=max(res,ans);//如果全部装完了背包里还没有装满5个，返回ans. 
    return dp[top[0]][top[1]][top[2]][top[3]]=ans;
}

int main(){
    int book[N];//用来存颜色是否出现，所以不能用全局数组，因为会随条件的改变而改变，现在函数中当做变量。 
    while(cin>>n&&n){
        res=0;
        ans=0;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=4;j++){
                cin>>p[i][j];
            }
        }
        memset(dp,0,sizeof(dp));//初始化 
        memset(top,0,sizeof(top));
        memset(book,0,sizeof(book));
        dfs(0,book);//包里有0个糖果 
        cout<<res<<endl;
    }
    return 0;
}