动态规划练习题(背包问题)
The King’s Ups and Downs
关于公式推导的动态规划
The king has guards of all different heights. Rather than line them up in increasing or decreasing height order, he wants to line them up so each guard is either shorter than the guards next to him or taller than the guards next to him (so the heights go up and down along the line). For example, seven guards of heights 160, 162, 164, 166, 168, 170 and 172 cm. could be arranged as:

or perhaps:

The king wants to know how many guards he needs so he can have a different up and down order at each changing of the guard for rest of his reign. To be able to do this, he needs to know for a given number of guards, n, how many different up and down orders there are:
For example, if there are four guards: 1, 2, 3,4 can be arrange as:
1324, 2143, 3142, 2314, 3412, 4231, 4132, 2413, 3241, 1423
For this problem, you will write a program that takes as input a positive integer n, the number of guards and returns the number of up and down orders for n guards of differing heights.
Input
The first line of input contains a single integer P, (1 <= P <= 1000), which is the number of data sets that follow. Each data set consists of single line of input containing two integers. The first integer, D is the data set number. The second integer, n (1 <= n <= 20), is the number of guards of differing heights.
Output
For each data set there is one line of output. It contains the data set number (D) followed by a single space, followed by the number of up and down orders for the n guards.
Sample Input
4
1 1
2 3
3 4
4 20
Sample Output
1 1
2 4
3 10
4 740742376475050
题目大意:给你一组不同身高的士兵,让你按高低高低高低或低高低高低高的方式排成一排,并输出这组的排列方式的数目。
解题思想:
当你增加一个数n并按题目方式加入前边n-1个数之间时,你可以有n个位置插入
1 2 3 4 5 6 7 加入n=8
0 1 2 3 4 5 6 7 可插8八个位置
当我们插入n时必须要满足它的前边高->低 - n - 低->高 因为加入的n是最大的。
如果我们我们取第i个位置插入那么前i位置以前共有i个数,那么这i个数将有C[n-1][i],即从前n-1个数中取i个数的可能方式数(排列组合)。
记录前边i个数中为高低排列的为dp[i][0],低高排列的为[i][1],由对称性可知两个是相等的且等于sum[i]/2.
那么可以得到公式
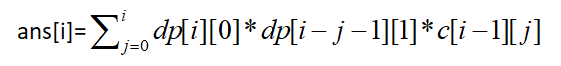
AC代码:
#include <iostream>
#include <cmath>
using namespace std;
typedef long long ll;
ll c[100][100];
ll dp[25][2];
ll sum[100];
void solve(){
ll t=0;
dp[0][0]=1;
dp[0][1]=1;
dp[1][0]=1;
dp[1][1]=1;
for(int i=2;i<=22;i++){
t=0;
for(int j=0;j<i;j++){
t+=dp[j][0]*dp[i-1-j][1]*c[i-1][j];
}
sum[i]=t;
dp[i][0]=dp[i][1]=t>>1;
}
return ;
}
int main(){
ll n,a,b;
for(int i=0;i<=22;i++){
c[i][0]=c[i][i]=1;
}
c[1][1]=1;
for(int i=2;i<=22;i++){
for(int j=1;j<i;j++){
c[i][j]=c[i-1][j-1]+c[i-1][j];
}
}
sum[0]=0;
sum[1]=1;
solve();
cin>>n;
while(n--){
cin>>a>>b;
cout<<a<<" "<<sum[b]<<endl;
}
}
Tickets
简单的公式推导,找这一项与前边项的关系
现在有n个人要买电影票,如果知道每个人单独买票花费的时间,还有和前一个人一起买花费的时间,问最少花多长时间可以全部买完票。
Input
给出 N(1<=N<=10),表示有N组样例给出K (1<=K<=2000),表示有K个人买票.. 给出K个数表示这个人单独买票会花的时间..保证每个数 (0s<=Si<=25s)给出K-1个数,表示这个人和前面那个人一起买票会花的时间..保证每个数 (0s<=Si<=50s)
Output
对于每一组数据,你需要给出电影院售票结束的时间,售票开始的时间为 08:00:00 am. 时间格式为: HH:MM:SS am|pm. 具体看样例输出
Sample Input
2
2
20 25
40
1
8
Sample Output
08:00:40 am
08:00:08 am
解题思路:
推出递推公式即可ans[i]=min((ans[i-1]+arr[i]),ans[i-2]+arr1[i]);
代码:

#include <bits/stdc++.h>
using namespace std;
int arr[2500];
int arr1[2500];
int ans[2500];
int main(){
int n,k;
int h,m,s;
cin>>n;
while(n--){
string hh,mm,ss,cc;
ostringstream s1,s2,s3;
memset(ans,0,sizeof(ans));
cin>>k;
for(int i=1;i<=k;i++){
cin>>arr[i];
}
for(int i=2;i<=k;i++){
cin>>arr1[i];
}
ans[1]=arr[1];
for(int i=2;i<=k;i++){
ans[i]=min((ans[i-1]+arr[i]),ans[i-2]+arr1[i]);
}
h=ans[k]/3600+8;
m=(ans[k]%3600)/60;
s=(ans[k]%3600)%60;
if(h>=12)
cc="pm";
else cc="am";
s1<<h;
hh = s1.str();
s2<<m;
mm=s2.str();
s3<<s;
ss=s3.str();
if(hh.size()==1){
hh.insert(0,1,'0');
}
if(mm.size()==1){
mm.insert(0,1,'0');
}
if(ss.size()==1){
ss.insert(0,1,'0');
}
cout<<hh<<":"<<mm<<":"<<ss<<" "<<cc<<endl;
}
return 0;
}
钱币兑换问题
完全背包问题,求得是放入的方式数目。
在一个国家仅有1分,2分,3分硬币,将钱N兑换成硬币有很多种兑法。请你编程序计算出共有多少种兑法。
Input
每行只有一个正整数N,N小于32768。
Output
对应每个输入,输出兑换方法数。
Sample Input
2934
12553
Sample Output
718831
13137761
解题思路:
完全背包问题,存的不是价值而是出现的次数,类似。
代码:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll arr[40000];
void dp(){
arr[0]=1;
for(int j=1;j<=3;j++)
for(int i=1;i<=35000;i++){
arr[i]+=arr[i-j];
}
return ;
}
int main(){
int n;
dp();
while(cin>>n){
cout<<arr[n]<<endl;
}
return 0;
}
01背包的路径问题:
在存放物品的时候,建立一个数组,来判断有没有在vis[i][j]的情况下取出第i件物品。在回溯的时候,从最大值开始,判断他的值是否与他上边的值相同,即判断他有没有在最有情况下被取出。如果有继续在上一层找,其中j变为j-w[i]。
参考:m[n][c]为最优值,如果m[n][c]=m[n-1][c] ,说明有没有第n件物品都一样,则x[n]=0 ; 否则 x[n]=1。当x[n]=0时,由x[n-1][c]继续构造最优解;当x[n]=1时,则由x[n-1][c-w[i]]继续构造最优解。以此类推,可构造出所有的最优解。(这段全抄算法书,实在不知道咋解释啊。)
例题:
CD
You have a long drive by car ahead. You have a tape recorder, but unfortunately your best music is on CDs. You need to have it on tapes so the problem to solve is: you have a tape N minutes long. How to choose tracks from CD to get most out of tape space and have as short unused space as possible.
Assumptions:
• number of tracks on the CD does not exceed 20
• no track is longer than N minutes
• tracks do not repeat
• length of each track is expressed as an integer number
• N is also integer
Program should find the set of tracks which fills the tape best and print it in the same sequence as the tracks are stored on the CD
Input
Any number of lines. Each one contains value N, (after space) number of tracks and durations of the tracks. For example from first line in sample data: N = 5, number of tracks=3, first track lasts for 1 minute, second one 3 minutes, next one 4 minutes
Output
Set of tracks (and durations) which are the correct solutions and string ‘sum:’ and sum of duration times.
Sample Input
5 3 1 3 4
10 4 9 8 4 2
20 4 10 5 7 4
90 8 10 23 1 2 3 4 5 7
45 8 4 10 44 43 12 9 8 2
Sample Output
1 4 sum:5
8 2 sum:10
10 5 4 sum:19
10 23 1 2 3 4 5 7 sum:55
4 10 12 9 8 2 sum:45
题目大意:
在旅途中听音乐的时候,他要先按顺序放好cd,然后按顺序播放,要求在给定的最大时间内,他能听音乐的最大时间,要求一整首要放完。
解题思路:
01背包问题,加上了回溯。
代码:

#include <iostream>
#include <string.h>
using namespace std;
const int N=1e6;
int w[N];
int dp[N];
int vis[50][N];
int main(){
int W,n;
while(cin>>W>>n){
memset(dp,0,sizeof(dp));
memset(vis,0,sizeof(vis));
for(int i=n;i>=1;i--){//倒序输入
cin>>w[i];
}
for(int i=1;i<=n;i++){
for(int j=W;j>=w[i];j--){
dp[j]=max(dp[j],dp[j-w[i]]+w[i]);//01背包模板
if(dp[j]==dp[j-w[i]]+w[i]){
vis[i][j]=1;//标记该物品在这个状态下有没有被装到背包里
}
}
// for(int j=1;j<=W;j++){//可以看到加入背包的整个过程
// cout<<dp[j]<<" ";
// }
// cout<<endl;
}
int j=W,i=n;
for(;i>=1;i--){
if(vis[i][j]){
cout<<w[i]<<" ";//从最优状态下开始,判断第i个物品有没有装进背包,直到结束。
j-=w[i];
}
}
printf("sum:");
cout<<dp[W]<<endl;
}
return 0;
}
Robberies (HDU – 2955)
可怜的POIUYTREWQ最近想买下dota2的商品,但是手头缺钱。他想起了之前看过的一部大片,觉得抢银行也许是个不错的选择。他认为,坏人被抓是因为没有预先规划。于是他在之前的几个月对各大银行进行了一次评估; 评估内容包括安全性和可盗窃金额: 他想知道在在某个风险系数下可以偷窃的最大金额
Input
第一行给出了一个整数T, 表示有T组测试数据. 对于每一组数据,第一行给出了一个浮点数P, 表示POIUYTREWQ允许被抓的最大概率, 和一个整数N,表示他计划去抢劫的N个银行. 接下来N行, 每行给出一个整数数Mj和浮点数Pj.
抢劫银行 j 可获得 Mj 百万美金, 被抓的概率是 Pj .
Output
对于每组数据,每行输出一个整数,表示POIUYTREWQ在被抓概率小于P的情况下,可抢到的最多的金钱。
Notes and Constraints
0 < T <= 100
0.0 <= P <= 1.0
0 < N <= 100
0 < Mj <= 100
0.0 <= Pj <= 1.0
你可以认为每家银行都是独立的。
Sample Input
3
0.04 3
1 0.02
2 0.03
3 0.05
0.06 3
2 0.03
2 0.03
3 0.05
0.10 3
1 0.03
2 0.02
3 0.05
Sample Output
2
4
6
解题思路:
01背包问题,可以认为是偷最多的钱的逃跑概率。然后倒着遍历最后的dp数组,来判断当恰好能逃跑时最多能偷多少钱。
Ac代码:

#include <bits/stdc++.h>
using namespace std;
const int N=10000+100;
double dp[N];
int w[N];//每个银行能得到的钱
double v[N];//逃跑概率
int main(){
double t,z,p;
int n,sum=0;
cin>>t;
while(t--){
memset(dp,0,sizeof(dp));
sum=0;
cin>>z>>n;
for(int i=1;i<=n;i++){
cin>>w[i]>>v[i];
v[i]=1-v[i];
sum+=w[i];//能偷得最多的钱
}
p=1-z;//逃跑概率
dp[0]=1;
for(int i=1;i<=n;i++){
for(int j=sum;j>=w[i];j--){
dp[j]=max(dp[j],dp[j-w[i]]*v[i]);//找能逃跑时偷得最多的钱
}
}
for(int i=sum;i>=0;i--){//0也有,表示偷不到钱
if(dp[i]>=p){
cout<<i<<endl;
break;
}
}
}
return 0;
}


