用通俗的语言讲解复杂度
复杂度分析
复杂度分析是数据结构和算法中最重要的知识点,当然学这篇只是把门找到;反之,学不会它,你就永远找不到窍门。
为什么复杂度分析会这么重要?
这个要从宇宙大爆炸,呃,从数据结构与算法的本身说起。
我平常白天做梦的时候,总想着当当咸鱼,最好能带薪拉屎就能赚大钱那种,数据结构与算法虽然没有俺这么高大尚的梦想,但是它的出现也是跟我一样总想在更少的时间及更少的存储来提高效率呗。
可以从哪些方面来入手呢铁子们,CPU与RAM的消耗时间啊,通信的带宽时间啊,指令的数量啊,这么多,我不学了不学,没事呀,我们可以总结一套模型在理论上针对不同算法的情况得出对应标准,复杂度这不就来了,你可以总结下,关于输入数据量n的函数,是吧。
搞清楚为什么,怎么定义
那咋去度量"更少的时间和更少的存储",复杂度分析由此而生。
打个不恰当的比方
如果把数据结构与算法看做武功招式,那复杂度分析就是对应的心法。
如果只是学会了数据结构与算法的用法,不学复杂度分析,这就和你费尽千辛万苦在隔壁老王家次卧进门右手地砖下偷挖出老王答辩村里无敌手的村林至宝王霸拳,然鹅发现秘籍上只有招式,你却没学会隐藏的心法口诀。
铁汁:哇,厉害厉害厉害,你胖你说都对,但还是没必要学啊。
小希:???
铁汁:现在很多网站啊包啊,代码随便跑一下,就能轻轻松松知道多少时间占了多少内存啊,算法的效率不就轻松对比出来了么?
小希:。。。。
two羊吐森破,吃葡萄不吐葡萄皮!
你们说的这种主流叫做事后分析法。
简单来说,就是你需要提前写好算法代码和偏好测试数据,然后在计算机上跑,通过最后得出的运行时间判断算法时效的高低水平,这里的运行时间就是我们日常的时间。
我且不用"万一你费劲心思写好的算法代码本身是个很糟糕的写法"这种理由反驳你,事后统计法本身存在缺陷,它并不是一个对我们来说有用的度量指标:
首先,事后统计法太依赖计算机的软件和硬件等性能。代码在corei7处理器的就比corei5处理器的运算速度快,更不用说不同的操作系统,不同的编程语言等软件方面,就算在同一台电脑上,前面的条件都满足,当时的内存或者CPU的使用率也会造成运行时的差异。
举个例子,考察对全国人口普查数据的排序n=10^9n=109,使用冒泡排序(10^9)^2(109)2
对于普通电脑(1GHz10^9109flops)来说,大约需要10^9109秒(30年)。
对于天河1号超级计算机(千万亿次=1P,$10^15$flops),大约需要10^3103秒(20分钟)。
再者,事后统计法太依赖测试数据集的规模。同样是排序算法,你随便整5个10个数排序,就算最垃圾的排序,也看起来很快跟火箭一样,不好意思,那10w个100w个,那这些算法的差距就很大了,而且同样是10w个100w个数,顺序和乱序的所花费时间也不等。
那问题来了,到底测试数据集选多少才合适?数据的顺序如何订好多才行?
可以看出,我们需要一个不依赖性能和规模等外力影响就可以估算算法效率,判断算法优劣的度量指标,而复杂度分析天生就是干这个的,为了能自己分析,所以你必须理解要掌握
时间复杂度
算法的运行时间
对于某一问题的不同解决算法。运行时间越短算法效率越高,相反,运行时间越长,算法效率越低。
那么如何估计算法复杂度?
所有人撤退,我们很熟悉的大O闪亮登场!
大佬们甩掉脑阔上最后一根秀发的才发现,当用运行时间去描述一个算法快慢的时候,算法中执行的总步数显得尤为重要。
因为这只是估算,我们假设每一行代码的运行时间都为Btime(一个比特时间),那么算法的总的运行时间=运行的总代码行数。
下面我们看一段简单的代码。
- //python
- deflonggege_sum(m);
- sum=0;
- forlonggegeinrange(m);
- sum+=longgege
- returnsum;
在上面假设的情况下,这段求累加和的代码总的运行时间是多少呢?
第二行代码需要1Btime的运行时间,第4行和第5行分别运行了m次,所以每个需要m*Btime的运行时间,所以总的运行时间就是(1+2m)*Btime。
若我们用S函数来表示赋值语句的总运行时间,所以上面的时间可表达成S(m)=(1+2m)*Btime,说人话就是"数据集大小"为m,总的步数为(1+2m)的算法执行时间为S(m)"。
上面的公式得出,S(m)和总步数是成正比关系,这个规律很重要的,告诉了一个易懂的趋势,数据规模和运行时间之间有趋势!
可能你对数据规模还是没有概念,类比下
对于我们现在的家用计算机,如果想在1s之内解决问题:
O(n^2n2)的算法可以处理大约10^4104级别的数据
O(n)的算法可以处理大约10^8108级别的数据
O(nlogn)的算法可以处理大约10^7107级别的数据
大O表示法
什么是大O
很多铁子说时间复杂度的时候你都知道O(n),O(n^2n2),但是说不清什么是大O
算法导论给出的解释:大O用来表示上界的,上界意思说对任意数据输入的算法最坏情况或叫最长运行时间。
拿插入排序来讲,它的时间复杂度我们都说是O(n^2),假如数据本来有序的情况下时间复杂度是O(n),也就对于所有输入情况来说,最坏是O(n^2)的时间复杂度,所以称插入排序的时间复杂度为O(n^2)。
就是想告诉你,同一个算法的时间复杂度不是一成不变的,和输入的数据形式依然有关系,数据用例不一样,时间复杂度也是不同的,这个要铭记住。还有平时面试官和我们探讨一个算法的实现以及性能,指的通常是理论情况下的时间复杂度。
铁子:我读书少,你可别骗我,你这还是有些抽象啊,而且你这适用所有的算法吗,未必吧
小希:你很有精神,你知道前n项和怎么算不。
铁子:这个我们初中老师讲过的,等差可以算
小希:你就看好下面,这段码
举栗子
- //计算1+2+3+....+n的和
- intsum=0
- for(inti=1;i<=n;i++){
- sum+=i
- }
可以看到循环了n次吧,所以时间复杂度就是O(n),即时间复杂度就是本程序计算的次数。
假如我们自己修改后的运行次数函数中,我们只去保留最高阶项
如果最高阶存在且不是1,则去除与这个项相乘的常数,是如下表达式:
2n^2+3n+1->n^2
所以时间复杂度为n^2n2
你可能疑问,为啥会去掉这些值,请看下图
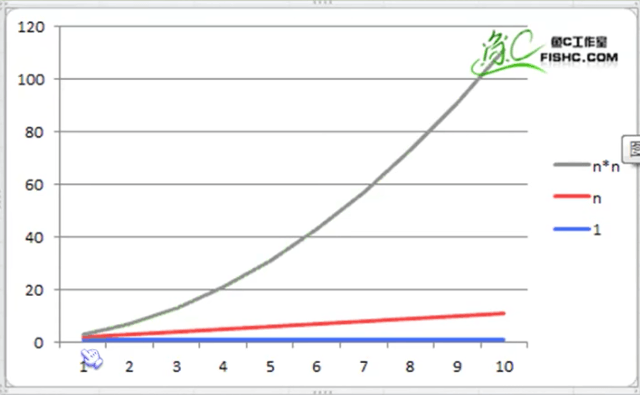
当计算量随着次数原来越大的时候,n和1的区别不是太大,而n^2n2曲线变得越来越大,所以这也是2n^2n2+3n+1->n^2n2最后会估量成n^2n2的原因,因为3n+1随着计算次数变大,基本可以忽略不计。
铁子:就这,你来个稍微复杂点的吧
安排
- //利用sums方法求三部分和
- //java
- publicstaticintsums(intn){
- intnum1=0;
- for(intlongege1=1;longege1<=n;longege1++){
- num1=num1+longege1;
- }
- intnum2=0;
- for(intlongege2=1;longege2<=n;longege2++){
- for(inti=0;i<=n;i++){
- num2=num2+longege2;
- }
- }
- intnum3=0;
- for(intlongege3=1;longege3<=n;longege3++){
- for(inti=0;i<=n;i++){
- for(intj=0;j<=n;j++){
- num3=num3+longege3;
- }
- }
- }
- returnnum1+num2+num3;
- }
上面这段是求三部分的和,经过之前的学习应该很容易知道,第一部分的时间复杂度是O(n),第二部分的时间复杂度是O(n^2n2),第三部分是O(n^3n3)。
正常来讲,这段代码的S(n)=O(n)+O(n^2n2)+O(n^3n3),按照我们按"主导"部分,显然前面两个兄弟都直接帕斯掉,最终S(n)=O(n^2n2)。
通过这几个例子,聪明的铁子们肯定会发现,对于时间复杂度分析来说,只要找出"主导"作用的部分代码即可,这个主导就是最高的那个复杂度,也就是执行次数最多的那部分n的量级。
剩下的就是多加练习,有意识的多去练多去想,就可以和我一样帅气稳啦。
我来介绍几种几种阶~
常数阶O(1)
- functiontest($n){
- echo$n;
- echo$n;
- echo$n;
- }
没有循环的,不管$n是多少,它只运行3次,那么时间复杂度就是O(3),取为O(1)
线性阶O(n)
- for($i=1;$i<=$n;$i++){
- $sum+=$i
- }
平(立)方阶:o(n^2n2)/o(n^3n3)
- $sum=0;
- for($i=1;$i<=$n;$i++){
- for($j=1;$j<$n;$j++){
- $sum+=$j
- }
- }
两次循环,里面循环执行了n次,外层循环也执行了n次,所以时间复杂度为O(n^2),立方阶一样
特殊平方阶:O(n^2n2/2+n/2)->O(n^2n2)
- for(){
- for(){
- .....----------->n^2
- }
- }
- +
- for(){
- ------------>n
- }
- +
- echo$a+$b-------------->1
所以整体上计算次数为n^2+n+1,我们算时间复杂度为O(n^2)
对数阶:O(log2n)
- intlongege=1
- while(longege<m){
- longege=longege*2;
- }
还是根据之前讲的,我们先找"主导",在里面主导就是最后一行,只要算出它的时间复杂度,这段的时间复杂度就知道了。
这段说人话就是,乘多少个2就会>=m?
假设需要y个,那么相当于求:
$2^y=m$
即
y=log2m
所以上述代码的时间复杂度应该为O(log2m)。
但是这种对数复杂度来说,不管你是以2,3为底,还是以20为底,通通记作(logn)。这就要从对数的换底公式说起。
除了数据集规模会影响算法的运行时间外,"数据的具体情况"也会影响运行时间。
我们来看这么一段代码:
- publicstaticintfind_word(int[]arr,Stringword){
- intflag=-1;
- for(inti=0;i<=arr.length;i++){
- if(arr[i]==word){
- flag=i;
- }
- break;
- }
- returnflag;
- }
上面这段简单代码是要求字符变量word在数组arr中出现的位置,我用这段来解释"数据的具体情况"是什么意思。
变量word可能出现在数组arr的任意位置,假设a=['a','b','c','d']:
- 当word='a',正好是列表中的第1个,后面的不需要在遍历,那么本情况下的时间复杂度是O(1)。
- 当word='d'或者word='e',这两种情况是整个列表全部遍历完,那么这些情况下的时间复杂度是O(n)。
根据不同情况,我们有了最好情况时间复杂度,最坏情况时间复杂度和平均情况时间复杂度这三个概念。
下面看一段代码,我们分别从最好和最坏的情况下去分析其时间复杂度。
- //n表示数组array的长度
- intfind(int[]array,intn,intx){
- inti=0;
- intpos=-1;
- for(inti=0;i<n;i++){
- if(array[i]==x){
- pos=i;
- }
- }
- returnpos;
- }
这段代码的功能是,在一个无序的数组中,查找变量x出现的位置。如果没有找到就返回-1。笼统的分析一下:核心代码执行了n次,所以其时间复杂度是O(n),其中,n代表数组的长度。
代码简单优化一下:可以在中途找到符合条件的元素时,提前结束循环。
- //n表示数组array的长度
- intfind(int[]array,intn,intx){
- inti=0;
- intpos=-1;
- for(;i<n;i++){
- if(array[i]==x){
- pos=i;
- break;
- }
- }
- returnpos;
- }
优化完之后的代码就不能简单粗暴的说其时间复杂度就是O(n)了。因为,遍历可能在数组下标为0~n-1中的任何一个下标所指向的元素中结束循环,是不是很神奇。继续往下分析:
- 假设,数组中第一个元素正好是要查找的变量x,显而易见那时间复杂度就是O(1)。
- 假设,数组中不存在变量x,那我们就需要把整个数组遍历一遍,时间复杂度就成了O(n)。
所以,在不同的情况下,这段代码的时间复杂度是不同的。
这几个概念从我相信你从字面意思也能理解,最好时间复杂度就是,在最理想的情况下,执行这段代码的时间复杂度。对应假设1。时间复杂度就是O(1)。
同理,最坏时间复杂度就是,在最糟糕的情况下,执行这段代码的时间复杂度。对应假设2。时间复杂度就是O(n)。
平均时间复杂度
首先先来说它,又叫"加权平均时间复杂度",为什么叫加权呢?是不是很奇怪,因为,通常计算平均时间复杂度,需要把概率考虑进去,也就是,我们计算平均时间复杂度的时候,需要一个"加权值",来真正的计算平均时间复杂度。
我们整个代码例子,对平均时间复杂度进行分析:
- //n表示数组array的长度
- intfind(int[]array,intn,intx){
- inti=0;
- intpos=-1;
- for(;i<n;++i){
- if(array[i]==x){
- pos=I;
- break;
- }
- }
- returnpos;
- }
代码很简单,表示在一个数组中,要找到x这个数,最好复杂度是O(1),最坏是O(n)。
那平均复杂度是怎么计算呢?
先说简单的平均值计算公式:
上面的代码,所有查找x的时间相加:1+2+3+······+n+n(这个n表示当x不存在时遍历array需要的次数),另外,需要查找的次数为n+1次,那么结果就是:
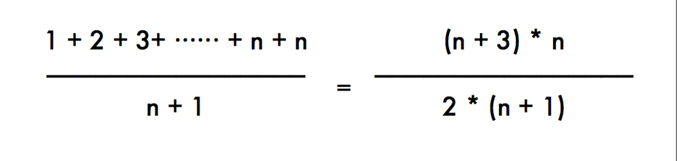
代入大O表达式,结果是O(n)。
这个公式表达的是:计算所有可能出现的情况之和,然后除以可能出现的情况的次数。说白了,这是一个绝对平均的结果。表示每个结果都可能出现n+1次。
这是一个较为粗暴的假设。
如果稍微使用一个简单的概率来计算呢?
这里有2个概率:
x变量是否在数组中的概率,有2种情况——在与不在,所以,他的概率是1/2;
x变量出现在数组的概率,有n种情况,但只会出现一次,所以是1/n。
我们把两个概率进行相乘,结果是1/(2n).这个数,就是"加权值"。
如何使用加权值对上面代码的"复杂度"进行计算?
然后,我们在这公式上把(n+1)换成"权重":也就是1/2n。
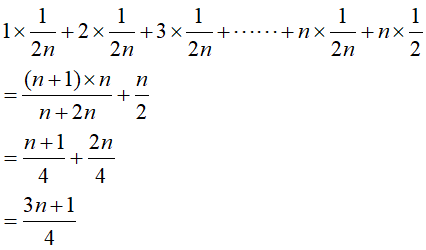
结果为3n+1/4。这个也就是"加权后的平均时间复杂度",表示,执行了1+2+····+n+n次的"加权平均值"。
如果使用大O表示法,去除系数,常数,低阶,那么他的最终结果就是O(n)。
可以看到,前者使用的是分母没有做任何权重的措施,仅仅是简单的n+1,而后者,我们做了简单的权重计算,认为出现的概率不是n+1,而是1/2n。
可以说,加权值,是为了在前者的基础上,,目的是更加的准确。也就是说,要计算准确的平均时间复杂度,就需要准确的计算这个"权重值",而权重值会受到数据范围,数据种类影响。因此需要在实际操作中,进行调参。
简单来说,就拿"x变量是否在数组中的概率"这个值来说,不一定是1/2,如果有这样一组数据{y,s,f,f,g,x,g,h},那么,他的概率还是1/2吗,实际上只有1/8,所以,还是得根据实际情况来。
均摊时间复杂度
啊这,听起来和平均时间复杂度有点熟悉呢。但是均摊时间复杂度的应用场景比平均时间复杂度更加特殊、更加有限。下面看一段代码:
- //array表示一个长度为n的数组
- //代码中的array.length就等于n
- staticint[]array=newint[]{1,2,3,4,5};
- staticintcount=2;
- publicstaticvoidinsert(intval){
- //数组没有空闲空间的情况
- if(count==array.length){
- intsum=0;
- for(inti=0;i<array.length;i++){
- sum=sum+array[i];
- }
- array[0]=sum;
- count=1;
- System.out.println("array.length:::"+array.length+"sum:"+sum);
- }
- //数组有空闲空间的情况
- array[count]=val;
- count++;
- System.out.println("count!=array.length:"+array.length+",,,count::"+count);
- for(inti=0;i<array.length;i++){
- System.out.println("array["+i+"]="+array[i]);
- }
- }
上面实现了向一个数组中插入数据的功能。当数组满了之后,也就是代码中的count==array.length时,我们用for循环遍历数组求和,并清空数组,将求和之后的sum值放到数组的第一个位置,然后再将新的数据插入。但如果数组一开始就有空闲空间,则直接将数组插入数组。
现在分析一下这段代码的时间复杂度,最理想的情况下,数组中有空闲空间,我们只需要将数据插入到下标为count的位置就可以了,所以最好情况时间复杂度为O(1)。最坏的情况下,数组中没有空闲空间了,我们需要先做一次数组的遍历求和,然后再将数据插入,所以最坏情况时间复杂度为O(n)。
接着我们按上面的方法分析一下平均时间复杂度。假设数组的长度是n,根据插入数据的位置不同,我们可以分为n种情况,每种情况的时间复杂度是O(1)。此外,还有一种:"额外"的情况,就是在数组没有空闲空间插入一个数据,这个时候的时间复杂度是O(n)。而且,这n+1中情况发生的概率是一样的,都是1/(n+1)。
其实,这个例子里的平均复杂度分析并不需要这么复杂,不需要使用概率的知识。我们先来对比一下这个insert()的例子和上面的find()的例子,二者的区别如下:
区别一:
首先,find()函数在极端情况下,复杂度才为O(1)。但insert()在大部分情况下,时间复杂度都为O(1)。只有个别情况下,复杂度才比较高哦,为O(n)。这是两者间的第一个区别。
区别二:
对于insert()函数来说,O(1)时间复杂度的插入和O(n)时间复杂度的插入,出现的频率是非常有规律的,而且有一定的前后时序关系,一般都是一个O(n)插入之后,紧跟着n-1个O(1)的插入操作,循环往复而已。
所以,针对这样一种特殊场景的复杂度分析,我们不需要像之前平均复杂度分析方法那样,找出所有的输入情况及相应的发生概率,然后再计算加权平均值,这种就没必要。
针对这种特殊的场景,我们引入一种更加简单的分析方法:摊还分析法,通过摊还分析得到的时间复杂度叫做均摊时间复杂度。
那究竟如何使用摊还分析法来分析算法的均摊时间复杂度呢?
继续看这个insert()的例子。每一次O(n)的插入操作,都会跟着n-1次O(1)的插入操作,所以把耗时多的那次操作均摊到接下来的n-1次耗时少的操作上,均摊下来,这一组连续的操作的均摊时间复杂度就是O(1)。这就是均摊分析的大致思路,可以吧?
对一个数据结构进行连续操作中,大部分情况下时间复杂度都很低,只有个别情况下时间复杂度比较高,而且这些操作之间存在前后连贯的时序关系,这个时候我们就可以把这一组操作放在一起来分析,看是否能将较高时间复杂度那次操作的耗时,平摊到其他那些时间复杂度比较低的操作上。而且,在能够应用均摊时间复杂度分析的场合,一般均摊时间复杂度就约等于最好情况时间复杂度。
总之,均摊是平均时间复杂度的极限情况
均摊时间复杂度可能不是很好理解,尤其是与平均时间复杂度的区别。但是,我们可以将其理解为一种特殊的平均时间复杂度。最主要的还是应该掌握它的分析方法,这种思想而已。
之所以引入这几个复杂度的概念,是因为,我们在同一段代码,在不同输入的情况下,复杂度量级有可能是不一样的。在引入这几个概念之后,我们可以更加全面的表示一段代码的执行效率。
平时大家更多的关心是最好的时间复杂度,这没错,提高时间效率吗没错
但
我觉得更关心最坏情况而不是最好情况,理由如下:
(1)最坏情况它能给出算法执行时间的上界,这样可以确信,无论给什么输入,算法的执行时间都不会超过这个上界,这样为比较和分析心里有个底。
(2)最坏情况是种悲观估计,但是对于很多问题,平均情况和最坏情况的时间复杂度相差不多,比如插入排序这个例子,平均情况和最坏情况的时间复杂度都是输入长度n的二次函数。
空间复杂度
空间复杂度跟时间复杂度相比,你需要掌握的内容不多。
也是一样,它也是描述的一种趋势,只不过这趋势是代码在运行过程中临时变量占用的内存空间。
嗯?临时吗
代码在计算机中的运行的存储占用,主要分成3部分
- 代码本身所占用的
- 输入数据所占用的
- 临时变量所占的
前两个它自己就是要必须占用空间,与代码的性能就没关系,所以最后衡量代码的空间复杂度,只关心在运行过程中临时占用的内存空间。
怎么算?
R(n)=O(f(n))
空间复杂度记作R(n),表示形式与时间复杂度S(n)一致。
分析下下面我们用一段简单代码来理解下空间复杂度。
- //python
- deflongege_ListSum(n):
- let=[]
- foriinrange(n):
- let.append(i)
- returnlet
上面这段中明显有两个临时变量let和i
let是建了一个空列表,这个列表占的内存会随着for循环的增加而增加,最大到n结束,所有呢,let的空间复杂度是O(n),i是存元素位置的常数阶,和规模n已经没有关系了,所以这段代码的空间复杂度为O(n)。
我们再来看下它O(n^2)
- //java
- publicstaticvoidlongege_ListSum(n){
- int[]arr1=newint[0];
- for(inti=0;i<=n;i++){
- intarr2=newint[0];
- for(intj=0;j<=n;j++){
- arr1.apend(arr2);
- }
- }
- returnarr1;
- }
还是一样的分析方式,很明显上面这的代码手动创建了一个二维数组arr1,一维占用n^2n2,所以它就是这段代码的空间复杂度啦。
那二分法是多少
- intselect(inta[],intk,intlen){
- intleft=0;
- intright=len-1;
- while(left<=right){
- intmid=left+((right-left)>>2);
- if(a[mid]==k){
- return1;
- }
- elseif(a[mid]>k){
- right=mid-1;
- } else {
- left=mid+1;
- }
- }
- returnNULL;
- }
代码中的k、len、a[]所分配的空间都不随着处理数据量变化,因此它的空间复杂度S(n)=O(1)
顺便说下

在最坏的情况下循环x次后找到,n/(2^x2x)=1;x=log2n;它的时间复杂度就是log2n。
在斐波那契数求空间复杂度的过程中,需要去考虑函数栈帧的过程,比如当我们求第五个斐波那契数的时候,这时候需要先开辟空间存放第四个数,然后再开辟空间存放第三个数;当开辟空间到第二个和第一个数的时候,第三个数得到结果并返回到第四个数中,第四个数的值已知后返回到第五个数,过程里面,最大占用空间即为层数减一。
开辟空间的大小最多等于层数+1,也就是说求第N个斐波那契数,空间复杂度即为O(N)。
递归算法的时间复杂度
1)一次递归调用,如果递归函数中,只进行一次递归调用,并且递归深度是depth,那么每个递归函数,它的时间复杂度为T,则总体的时间复杂度为O(T*depth)。
比如说,二分搜索法的递归深度是logn(每次都是对半分),则复杂度是O(Tlogn)。
总结个公式就是,递归的时间复杂度=递归总次数*每次递归的次数,空间复杂度=递归的深度(即树的高度)
2)两次递归调用(关注递归调用次数)
我们先看下面这个例子
- intf(intn){
- assert(n>=0);
- if(n==0)
- return1;
- else
- returnf(n-1)+f(n-1);
- }
怎样才能知道它的递归次数呢,我们可以画一棵递归树,再把树的节点数出来
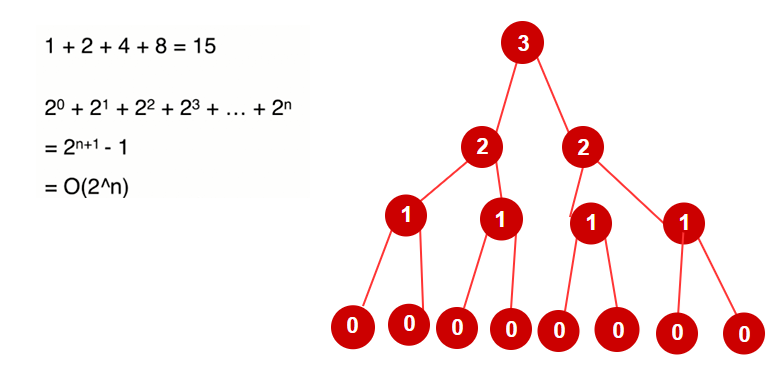
可以看到,这是指数级的算法,很慢很慢的!但这在我们的搜索领域是有很大的意义的。
但是我们的高级排序算法如,归并,快排也是2次递归调用,但时间复杂度只有O(nlogn)级别,那是因为
1)上面的深度为n,而高级排序的深度都只有logn;
2)在高级排序算法中我们在每个节点处理的数据规模是组件缩小的。
斐波那契数列的优化
斐波那契数列循环算法:
- //时间复杂度:O(n)
- //空间复杂度:O(1)
- longlongFib(longN){
- longlongfirst=1;
- longlongsecond=1;
- longlongret=0;
- inti=3;
- for(;i<=N;++i){
- ret=first+second;
- first=second;
- second=ret;
- }
- returnsecond;
- }
- intmain(){
- printf("%u\n",Fib(50));
- system("pause");
- return0;
- }
- //斐波那契数列递归算法:
- //时间复杂度:O(2^n)
- //空间复杂度:O(n)
- longlongFib(longlongN){
- return(N<3)?1:Fib(N-1)+Fib(N-2);
- }
- intmain(){
- printf("%u\n",Fib(1,1,50));
- system("pause");
- return0;
- }
注意:
斐波那契数列的时间复杂度为二叉树的个数;
斐波那契数列的时间复杂度为函数调用栈的次数即二叉树的深度。
斐波那契尾递归算法:(优化)
- //时间复杂度:O(n)
- //空间复杂度:O(n)
- longlongFib(longlongfirst,longlongsecond,intN){
- if(N<3) {
- return1;
- }
- if(N==3) {
- returnfirst+second;
- }
- returnFib(second,first+second,N-1);
- }
使用矩阵乘方的算法再次优化斐波那契数列算法。
- staticintFibonacci(intn){
- if(n<=1)
- returnn;
- int[,]f={{1,1},{1,0}};
- Power(f,n-1);
- returnf[0,0];
- }
- staticvoidPower(int[,]f,intn){
- if(n<=1)
- return;
- int[,]m={{1,1},{1,0}};
- Power(f,n/2);
- Multiply(f,f);
- if(n%2!=0)
- Multiply(f,m);
- }
- staticvoidMultiply(int[,]f,int[,]m){
- intx=f[0,0]*m[0,0]+f[0,1]*m[1,0];
- inty=f[0,0]*m[0,1]+f[0,1]*m[1,1];
- intz=f[1,0]*m[0,0]+f[1,1]*m[1,0];
- intw=f[1,0]*m[0,1]+f[1,1]*m[1,1];
- f[0,0]=x;
- f[0,1]=y;
- f[1,0]=z;
- f[1,1]=w;
- }
优化之后算法复杂度为O(log2n)。
总结
请背下来
算法刷题过程中,我们会遇到各种的时间复杂度,但就算你代码变出花来,几乎也逃不出下面几种常见的时间复杂度。

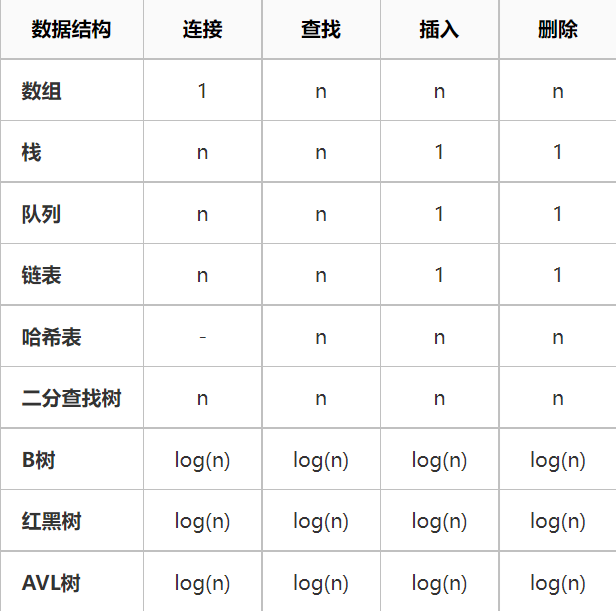
上表中的时间复杂度是由上往下依次增加,所以O(1)效率最高,O(n)和O(n^2n2)这两个前面已经说过了,上表最后一个效率低的离谱,以后要是不幸碰到我了在提一下,就不细说。
可能有些朋友还是疑惑,现在计算机硬件性能越来越强了,我们为啥还这么重视时间复杂度呢?
问的很好,我们可以用几个栗子来对比下,看下之间它们有多大的差距。
有100个人站在你面前,你一眼就发现了你喜欢的她。如果换成10000个,结果并没有什么区别。这就是O(1)
有100个人站在你面前,你得一个一个看过去,才能找到你的女神。无论你用什么顺序看,我总有一种办法,把你的女神放在你最后看到的那个。如果换成10000个,你就有了100倍的工作量。这就是O(n)
假如现在有100个人站在你面前,脸盲的你得两两结对、一对一对观察,才能找到唯一的一对双胞胎。同上,我总是可以把双胞胎放在你最后找到的一对。你至多一共要观察4950对。如果换成10000个,那就是49995000对,也就是10100倍的工作量这就是O(n²)
有128个人站在你面前,你要把他们按照高矮排序——我们假设用归并来解——你先把他们分成两个64人的大队,每个大队分成两个32人的中队,每个中队分成……直到最后每一个"小小…小队"只剩一个人。显然,一个人一定是已经排好序的。然后反向操作,将刚刚拆分的队伍合并起来。合并队伍的时候,由于已经排好序,只需要取出两队排头进行比较,就找到了最矮的一个,取出来——如此进行下去,合成的两倍大的队伍也将是有序的。显然,这个合并操作,是O(n)的。总共的比较次数,不会超过两个队伍的总人数。最后的问题只是,有多少次"分割-合并"操作。每次分割数量都减半,很明显是7次。由此看来,大致需要执行7×128次操作。这就是O(nlogn)
不同的时间复杂度,差距是明显的。
数据结构的时间复杂度
排序算法的时间复杂度
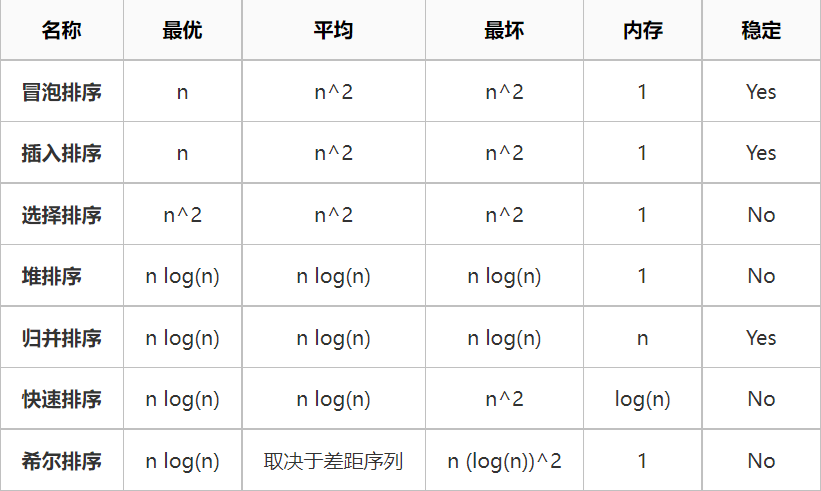
算法稳定性什么意思?如果排序前两个相等的数据其在序列中的先后位置顺序与排序后它们两个先后位置顺序相同,我们说算法具有稳定性,有什么意义呢?如果排序的算法是稳定的,第一个次排序的结果和关键字段可以为第二个次排序所用。
最后,算法和性能的关系,衡量一个算法的好坏,主要通过数据量大小来评估时间和空间,这些最后都直接会影响到程序性能,一般空间利用率小的,所需时间相对较长。所以性能优化策略里面经常听到空间换时间,时间换空间这样说法。
到这里,复杂度分析就全部讲完啦,只要你认真看完这篇文章,相信你会对复杂度分析有个基本的认识。复杂度分析本身不难,记得平时写代码的时候遇到问题有意识多估计一下自己的代码,感觉就会就会越来越熟悉的。
本文自华为云社区《用通俗的语言讲解复杂度》,作者: 龙哥手记 。
本文作者:莲藕淹,转载请注明原文链接:https://www.cnblogs.com/meanshift/p/16122856.html





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY