本文将介绍哈夫曼压缩算法(Huffman compression)。
1. 前文回顾
在字符串算法—字符串排序(上篇)和字符串算法—字符串排序(下篇)中,我们讲述了字符串的排序方法;
在字符串算法—字典树中,我们讲述了如何在一堆字符串中寻找某个字符串的方法;
在字符串算法—字符串搜索和字符串算法—正则表达式中,我们讲述了如何在一堆字符(如文章)中寻找某个特定的或符合某个规律的字符串的方法。
著名的压缩算法有很多,这里将介绍两个:哈夫曼压缩算法(Huffman compression)和LZW压缩算法(LZW compression)。
而本文将先讲述哈夫曼压缩算法(Huffman compression)。
2. 为什么要进行数据压缩
在这个每天都会诞生大量数据的时代,数据压缩扮演着重要的角色,如数据传输,传输压缩过的数据肯定会比原数据快。
数据压缩的重要性大家都懂,这里不多说,直接介绍如何进行数据压缩。
本文介绍的压缩算法是无损压缩,保证压缩解压后,数据无丢失。
3. 哈夫曼压缩算法(Huffman compression)
众所周知,计算机存储数据时,实际上存储的是一堆0和1(二进制)。
如果我们存储一段字符:ABRACADABRA!
那么计算机会把它们逐一翻译成二进制,如A:01000001;B: 01000010; !: 00001010.
每个字符占8个bits, 这一整段字符则至少占12*8=96 bits。
但如果我们用一些特殊的值来代表这些字符,如:
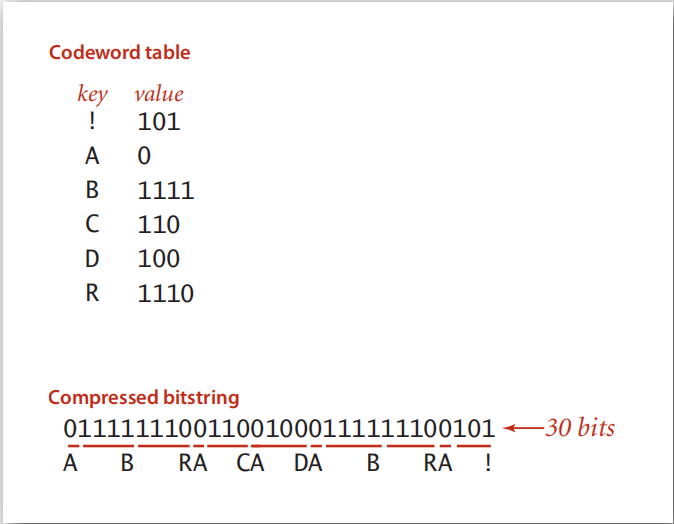
图中,0代表A; 1111代表B;等等。此时,存储这段字符只需30bits,比96bits小多了,达到了压缩的目的。
我们需要这么一个表格来把原数据翻译成特别的、占空间较少的数据。同时,我们也可以用这个表格,把特别的数据还原成原数据。
首先,为了避免翻译歧义,这个表格需满足一个条件:任何一个字符用的值都不能是其它字符的前缀。
我们举个反例:A: 0; B: 01;这里,A的值是B的值的前缀。如果压缩后的数据为01xxxxxx,x为0或者1,那么这个数据应该翻译成A1xxxxxx, 还是Bxxxxxxx?这样就会造成歧义。
然后,不同的表格会有不同的压缩效果,如:

这个表格的压缩效果更好。
那么我们如何找到最好的表格呢?这个我们稍后再讲。
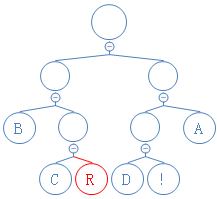
为了方便阅读,这个表格是可以写成一棵树的:

这棵树的节点左边是0,右边是1。任何含有字符的节点都没有非空子节点。(即上文提及的前缀问题。)
这棵树是在压缩的过程中建成的,这个表格是在树形成后建成的。用这个表格,我们可以很简单地把一段字符变成压缩后的数据,如:
原数据:ABRACADABRA!
表格如上图。
令压缩后的数据为S;
第一个字符是A,根据表格,A:11,故S=11;
第二个字符是B,根据表格,B:00,故S=1100;
第三个字符是R,根据表格,R:011,故S=1100011;
如此类推,读完所有字符为止。
压缩搞定了,那解压呢?很简单,跟着这棵树读就行了:
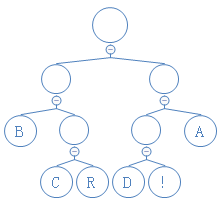
压缩后的数据S=11000111101011100110001111101
记住,读到1时,往右走,读到0时,往左走。
令解压后的字符串为D;
从根节点出发,第一个数是1,往右走:
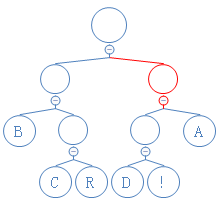
第二个数是1,往右走:
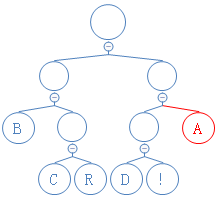
读到有字符的节点,返回此字符,加到字符串D里。D:A;
返回根节点,继续读。

第三个数是0,往左走:
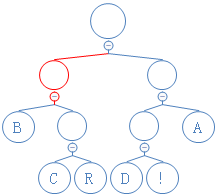
第四个数是0,往左走:
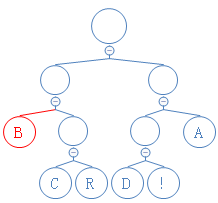
读到有字符的节点,返回此字符,加到字符串D里。D:AB;
返回根节点,继续读。
第五个数是0,往左走:
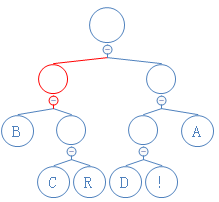
第六个数是1,往右走:
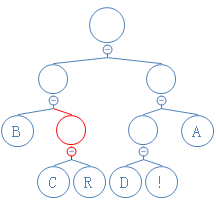
第七个数是1,往右走:
读到有字符的节点,返回此字符,加到字符串D里。D:ABR;
返回根节点,继续读。
如此类推,直到读完所有压缩后的数据S为止。
压缩与解压都搞定了,现在看如何构建这个表格:
我们需要先把原数据读一遍,并把每个字符出现的次数记录下来。如:
ABRACADABRA!中,A出现了5次;B出现了2次;C出现了1次;D出现了1次;R出现了2次;!出现了1次。
理论上,出现频率越高的字符,我们给它一个占用空间越小的值,这样,我们就可以有最佳的压缩率。
我们把这些字符,按次数的多少排成递增的顺序:(括弧中的数字为出现次数)

然后,我们把最小的两个字符找出来,并新建一个节点作为它们的父节点(谁左谁右不重要,随意):
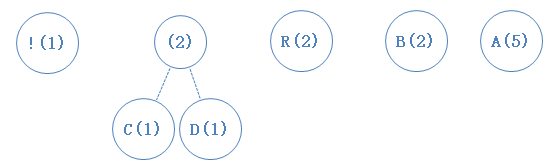
父节点的出现次数为子节点之和,新节点加入数组;(PS:这里提到了找出最小值,我们自然而然会想起了最小堆,不了解的,建议去补一下。用最小堆,我们可以高效地找出最小值,加入新元素也不需对数组重新排序)
然后,我们把最小的两个字符找出来,并从数组中移除,并新建一个节点作为它们的父节点(谁左谁右不重要,随意),新节点加入数组:
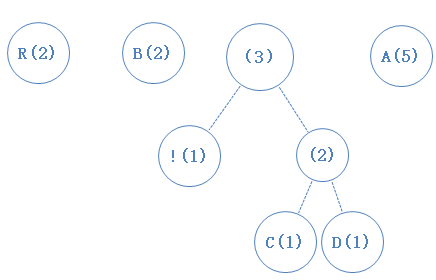
把最小的两个字符找出来,并从数组中移除,并新建一个节点作为它们的父节点(谁左谁右不重要,随意),新节点加入数组:

把最小的两个字符找出来,并从数组中移除,并新建一个节点作为它们的父节点(谁左谁右不重要,随意),新节点加入数组:
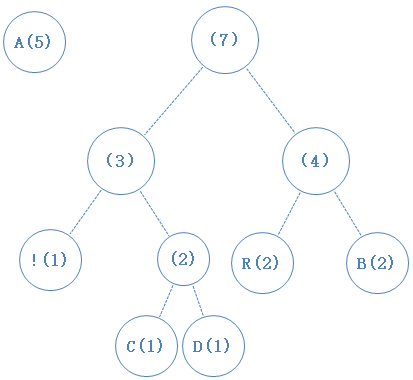
把最小的两个字符找出来,并从数组中移除,并新建一个节点作为它们的父节点(谁左谁右不重要,随意),新节点加入数组:
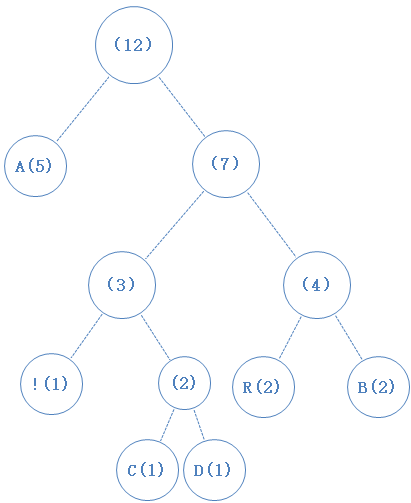
数组中只剩下一个元素了,构建表格结束。
把这棵树转成表格:
从左到右读过去(先序遍历)。给每个节点新建一个整数变量int C; 用C来记住每个节点对应的值。新建节点数组T来把含字符的节点记录下来。
从根节点出发,先看左子节点(左边是0,右边是1),发现含有字符A,故A对应的值为0。
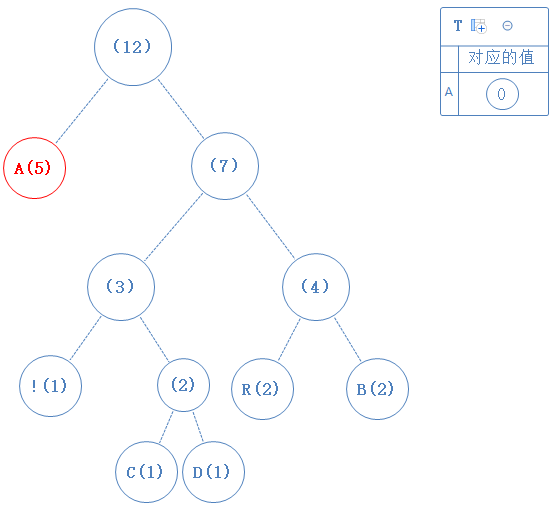
然后返回上一个父节点,再看右子节点,发现右子节点不含字符,此节点的值为1:
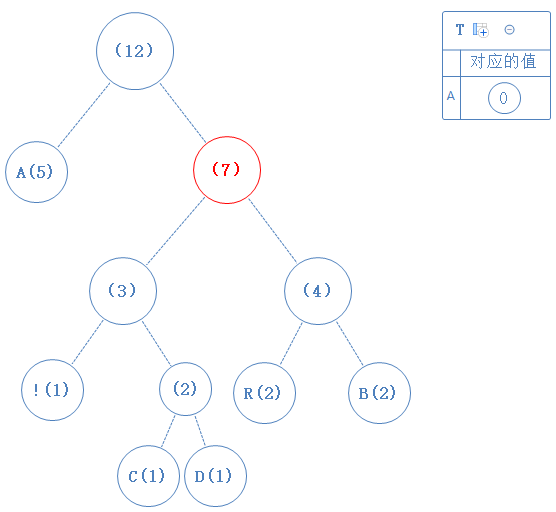
去看此节点的左子节点,发现此子节点不含字符,此节点的值为父节点的值+0,即10:(为了方便观看,我把代表频率的括弧里的值隐藏,把节点对应的值写在节点上)

去看此节点的左子节点,发现此子节点含符号 !,此节点的值为父节点的值+0,即100:
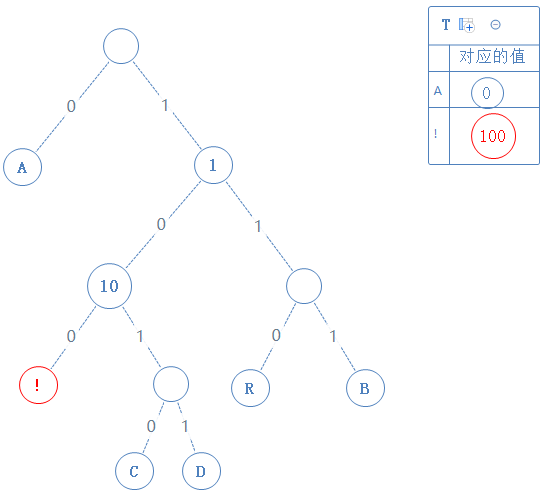
然后返回上一个父节点,再看右子节点,发现右子节点不含字符,此节点的值为父节点的值+1,即101:
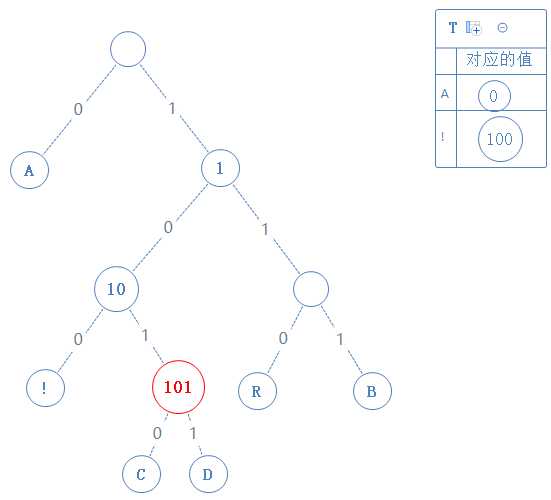
去看此节点的左子节点,发现此子节点含符号 C,此节点的值为父节点的值+0,即1010:
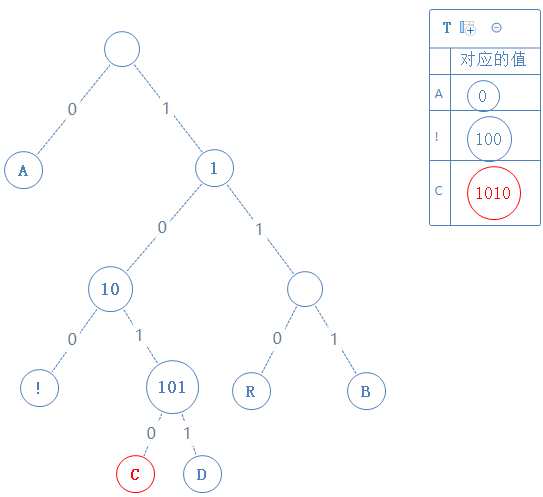
然后返回上一个父节点,再看右子节点,发现右子节点含字符D,此节点的值为父节点的值+1,即1011:
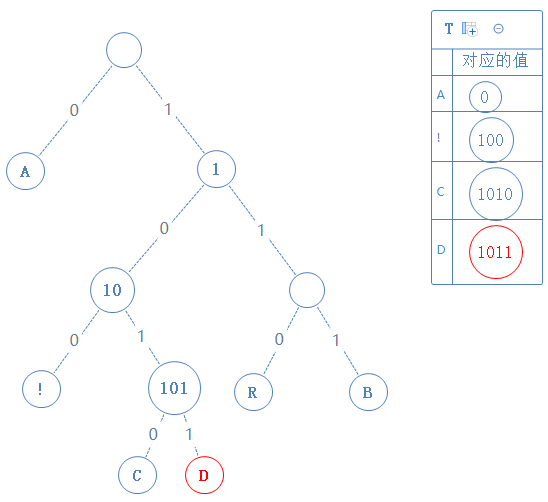
然后返回上一个父节点,左右子节点都看过了,再返回上一个父节点:
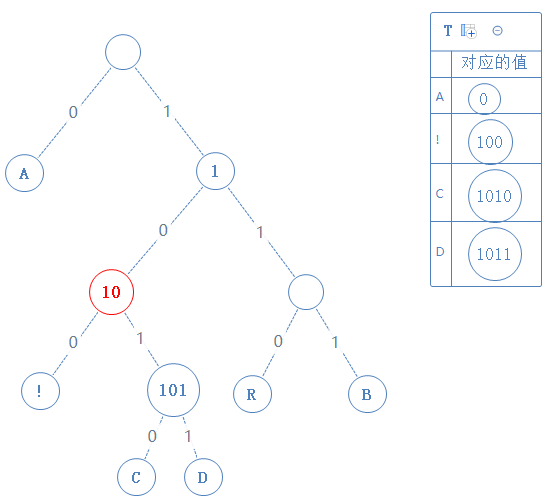
然后返回上一个父节点,再看右子节点,发现右子节点不含字符,此节点的值为父节点的值+1,即11:

去看此节点的左子节点,发现此子节点含符号 R,此节点的值为父节点的值+0,即110:
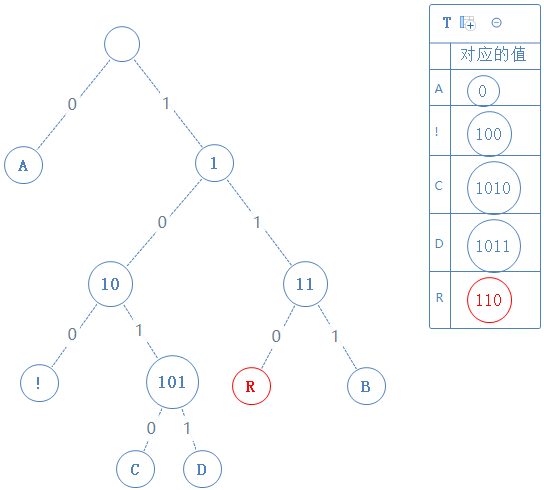
然后返回上一个父节点,再看右子节点,发现右子节点含字符B,此节点的值为父节点的值+1,即111:

然后一路返回父节点,去寻找有没还没看的子节点,结果没有,建表完成。
这个表格跟上述的例子用的表格不相同,如果用这个表格进行压缩,会发现压缩后的数据只有28bits。这个表格是最佳压缩表。
这个建表就是一个递归的过程。
到目前为止,我们已经讲了如何压缩、解压、建表。完事了吗?不,我们还需要把表格用二进制存储起来,并且能从二进制中读取表格。
存储表格跟上面的建表过程差不多,也是先序遍历(从左读到右)。
令表格存储的数据为Y;
首先从根节点开始:

此节点不含字符,故加一个0给Y,Y:0;
然后读此节点的左子节点:(为了避免歧义,我们把不含字符的点的值隐藏)
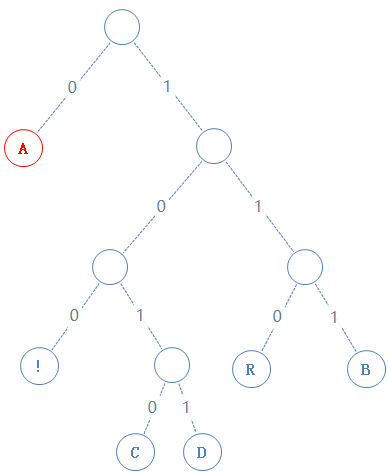
此节点含字符A,A的二进制为01000001,由于此节点含有字符,加一个1给Y,(这个1是标志着此节点含有字符),再把A的二进制加给Y,Y:0101000001;
然后返回上一个父节点,再看右子节点,发现右子节点不含字符,加一个0给Y,Y:01010000010;
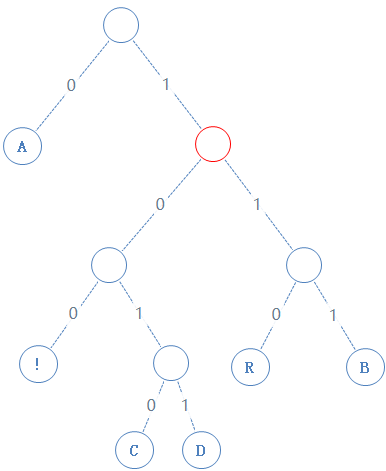
读此节点的左子节点,发现左子节点不含字符,加一个0给Y,Y:010100000100;
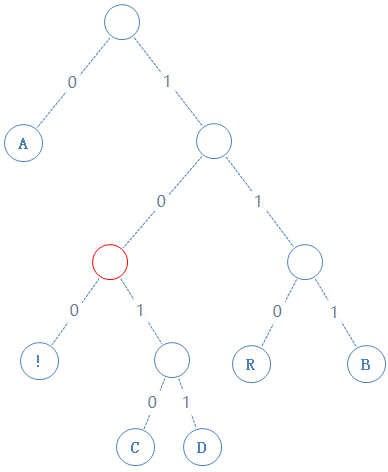
读此节点的左子节点:
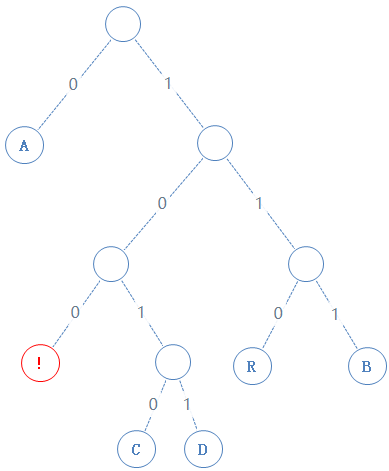
此节点含符号 !,!的二进制为00001010,由于此节点含有字符,加一个1给Y,再把 ! 的二进制加给Y,Y:010100000100100001010;
然后返回上一个父节点,再看右子节点,发现右子节点不含字符,加一个0给Y,Y:0101000001001000010100;
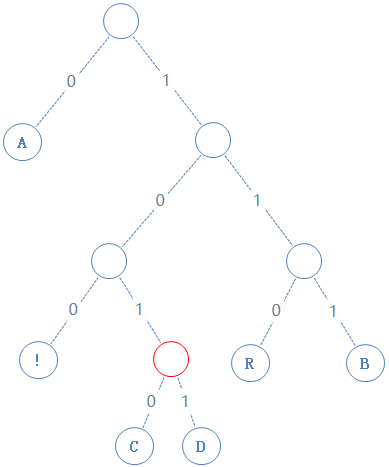
读此节点的左子节点:
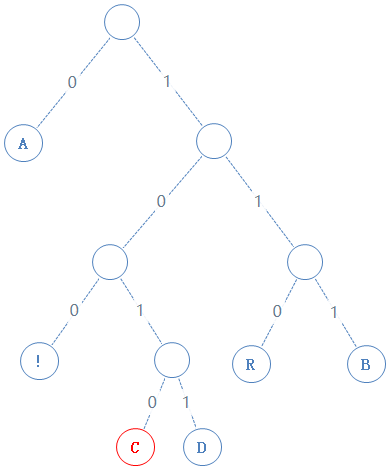
此节点含符号 C,C的二进制为01000011,由于此节点含有字符,加一个1给Y,再把C的二进制加给Y,Y:0101000001001000010100101000011;
然后返回上一个父节点,再看右子节点,发现右子节点含字符D,D的二进制为01000100,由于此节点含有字符,加一个1给Y,再把D的二进制加给Y,Y:0101000001001000010100101000011101000100;

然后返回上一个父节点,左右子节点都看过了,再返回上一个父节点:
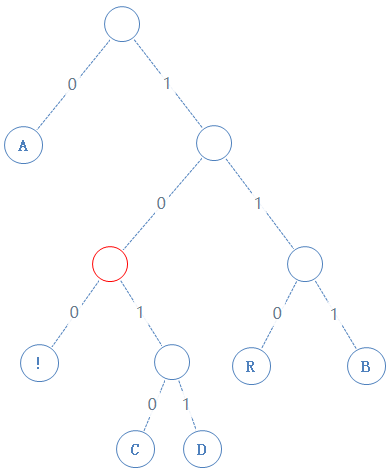
然后返回上一个父节点,再看右子节点,发现右子节点不含字符,加一个0给Y,Y:01010000010010000101001010000111010001000:
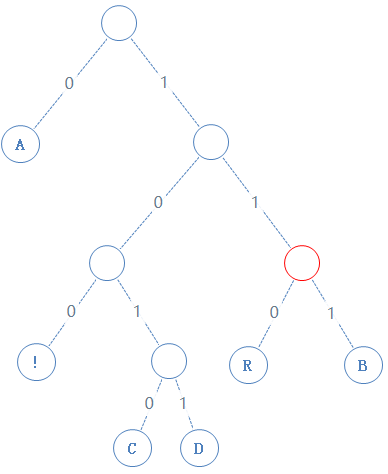
读此节点的左子节点:
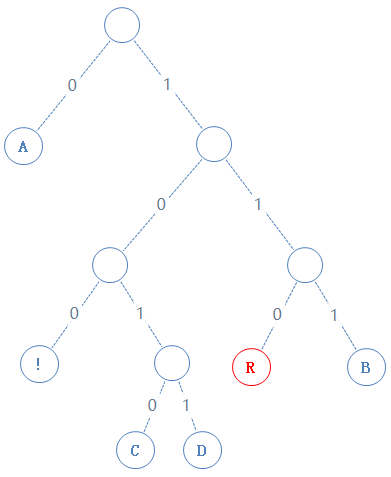
此节点含符号 R,R的二进制为01010010,由于此节点含有字符,加一个1给Y,再把R的二进制加给Y,Y: 01010000010010000101001010000111010001000101010010:
然后返回上一个父节点,再看右子节点,发现右子节点含字符B,B的二进制为01000010,由于此节点含有字符,加一个1给Y,再把B的二进制加给Y,Y: 01010000010010000101001010000111010001000101010010101000010;

然后一路返回父节点,去寻找有没还没看的子节点,结果没有,存储表格完成。
从二进制中读取表格也是用先序遍历(先左再右);
我们存储的表格数据为:Y: 01010000010010000101001010000111010001000101010010101000010;
第一个数字为0,说明这是不含字符节点,新建节点:

Y: 01010000010010000101001010000111010001000101010010101000010;
接下来新建的两个节点依次为此节点的左右节点;
第二个数字为1,说明这是含字符节点,读接下来的8个数字,得到对应的字符A,新建含A的节点;
Y: 01010000010010000101001010000111010001000101010010101000010;
下一个数字为0,说明这是不含字符节点,新建节点:
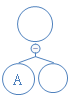
含A的节点没子节点;新建的不含字符的节点将把接下来新建的两个节点依次为此节点的左右节点;
Y: 01010000010010000101001010000111010001000101010010101000010;
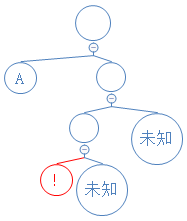
下一个数字为0,说明这是不含字符节点,新建节点:(未知节点的存在只是为了强调另一个节点为左节点)
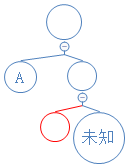
Y: 01010000010010000101001010000111010001000101010010101000010;
新建的不含字符的节点将把接下来新建的两个节点依次为此节点的左右节点;
下一个数字为1,说明这是含字符节点,读接下来的8个数字,得到对应的字符 ! ,新建含 ! 的节点;
Y: 01010000010010000101001010000111010001000101010010101000010;
下一个数字为0,说明这是不含字符节点,新建节点:

Y: 01010000010010000101001010000111010001000101010010101000010;
新建的不含字符的节点将把接下来新建的两个节点依次为此节点的左右节点;
下一个数字为1,说明这是含字符节点,读接下来的8个数字,得到对应的字符 C,新建含 C的节点;

Y: 01010000010010000101001010000111010001000101010010101000010;
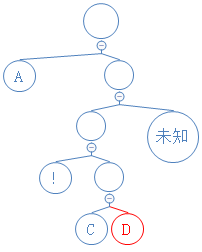
下一个数字为1,说明这是含字符节点,读接下来的8个数字,得到对应的字符 D,新建含 D的节点;
Y: 01010000010010000101001010000111010001000101010010101000010;
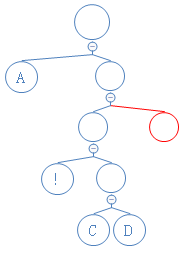
下一个数字为0,说明这是不含字符节点,新建节点,把节点放在未知节点处,(由于这个过程里,代码是使用递归,故自动把节点放在未知节点处)
Y: 01010000010010000101001010000111010001000101010010101000010;
新建的不含字符的节点将把接下来新建的两个节点依次为此节点的左右节点;
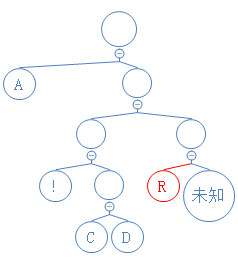
下一个数字为1,说明这是含字符节点,读接下来的8个数字,得到对应的字符 R,新建含 R的节点;
Y: 01010000010010000101001010000111010001000101010010101000010;
下一个数字为1,说明这是含字符节点,读接下来的8个数字,得到对应的字符 B,新建含B的节点;

Y: 01010000010010000101001010000111010001000101010010101000010;
读完,读表结束。
综上所述,哈夫曼压缩算法结束。
代码实现:
实现节点:
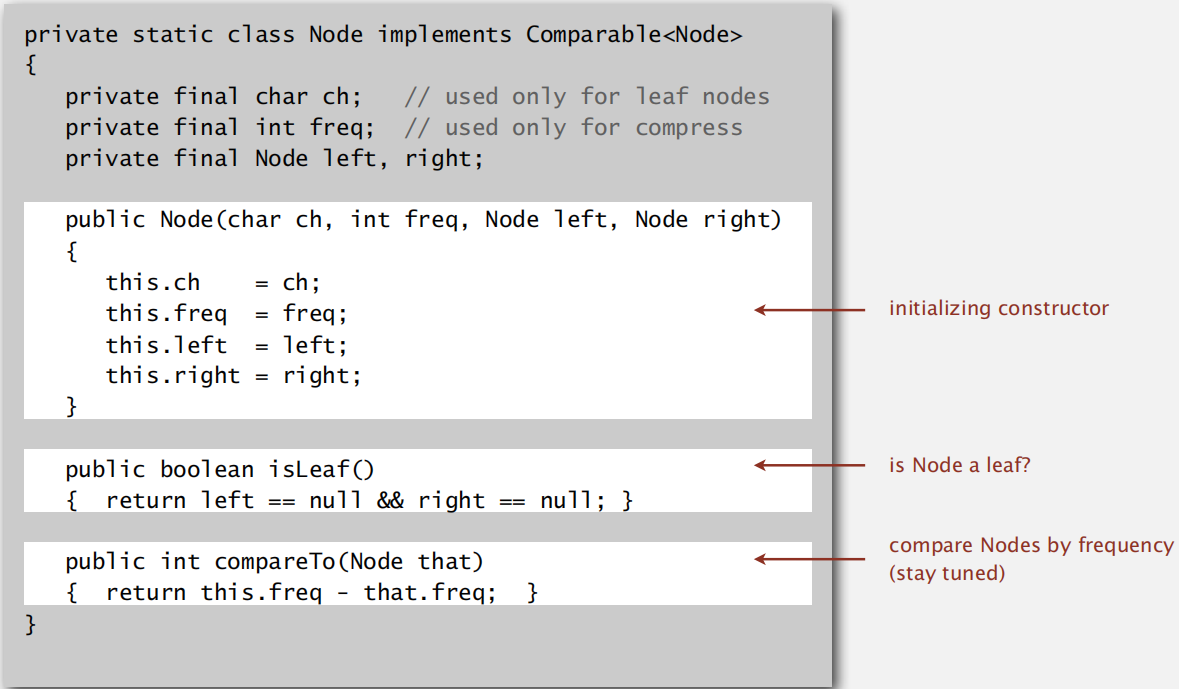
建立表格:
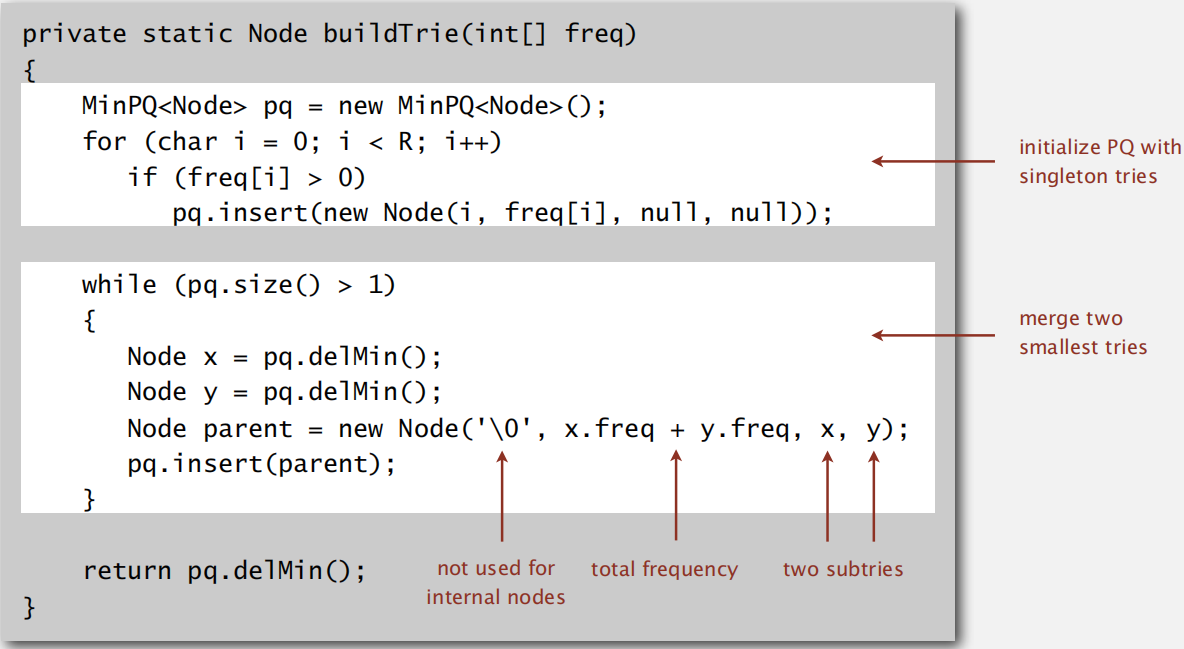
存储表格:

读取表格:
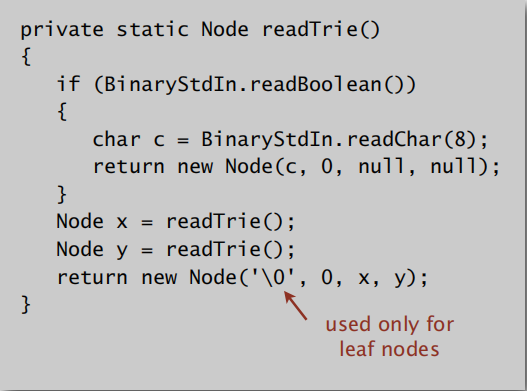
解压:
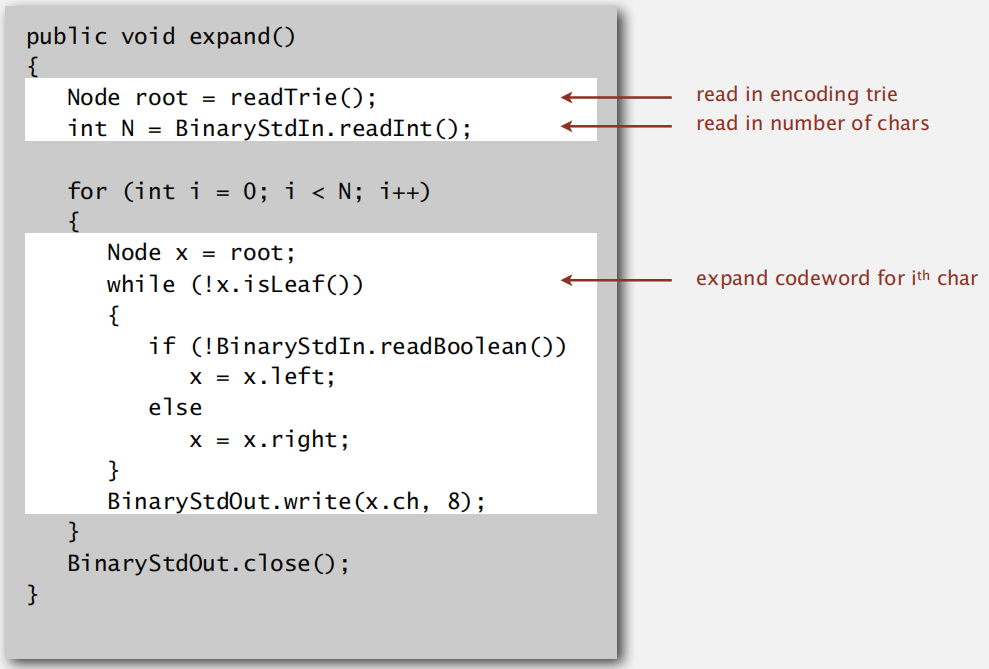
4. 算法缺点
哈夫曼压缩算法效率不错,美中不足之处为它建立表格时,需要先把原数据读一遍,从而来记录字符出现次数。这难免会对效率有所影响,我们是否会有更好的压缩算法呢?
是的,LZW压缩算法(LZW compression)将在下一篇随笔中介绍。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号