本文将介绍键索引计数法、LSD基数排序、MSD基数排序。
1. 字符串(String)
我们来简单回顾一下字符串。
众所周知,字符串是编程语言中表示文本的数据类型。它是一堆字符的组合,如 String S="String"。
我们可以知道字符串的长度:S.length()=6;
可以知道某个位置的字符是什么:S[0]="S"; S[5]="g";
可以提取S中的一部分;
可以把两个字符串合并起来形成新字符串等等。
2. 字符串排序
如果我们要对一堆字符串像字典一样排序,怎么排?例如:
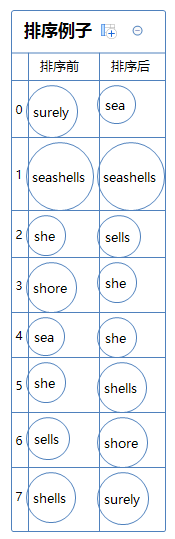
字典是怎么排序的呢?
按照英文字母表顺序a,b,c,d,...,y,w,我们得到了字母的大小排序:a<b<c<d<...<y<w。
sea和she相比,第一个字母相同,第二个字母e<h,故sea<she;
sea和seashells相比,前三个字母相同,但seashells比sea长,故sea<seashells;
seashells和sells相比,前两个字母相同,第三个字母a<l,故seashells<sells。
说到排序,我们自然想起了插入排序、归并排序、快速排序、堆排序,我们来回顾一下它们对N个对象进行排序的效率:

图中的CompareTo()就是对象之间比较大小的方法。
要想使用上述4种排序算法,必须提供一种对象之间比较大小的方法。即程序需要知道对象a与对象b谁大谁小(或相等)。
如果对象是数字,那比较方法容易实现。但如果对象是字符串,比较方法就复杂多了。
接下来,我们将介绍拥有比上述方法更高效率的字符串排序算法。
3. 键索引计数法(Key-indexed counting )
讲算法之前,我们来先了解一下这些算法的基础:键索引计数法。
从例子入手:a[]是拥有一堆只有一个字符的string数组。
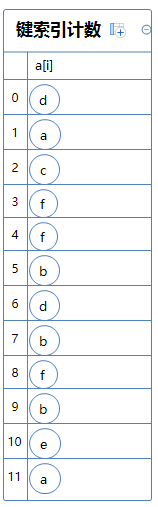
a[]中不同的字符分别有6个:a,b,c,d,e,f。我们需要给这些字符配对一些int类型的键索(Key-indexed):令a=0;b=1;c=2;d=3;e=4;f=5。
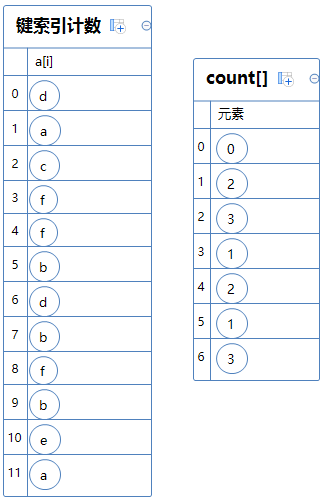
创建一个int类型的数组count,拥有7个元素:

然后我们数这六个字符分别重复出现了多少次,并把次数记录在count[x+1]中。x为某个字符对应的键索。
a重复出现了2次,a对应的键索为0,故count[1]=2;
b重复出现了3次,b对应的键索为1,故count[2]=3;
c重复出现了1次,c对应的键索为2,故count[3]=1;
d重复出现了2次,d对应的键索为3,故count[4]=2;
e重复出现了1次,e对应的键索为4,故count[5]=1;
f重复出现了3次,f对应的键索为5,故count[6]=3;
然后我们计算比某个字符小的字符有多少个,计算方法为count[x+1] += count[x]。x为某个字符对应的键索。(x从0开始逐渐递增)
例如:count[1]=count[1]+count[0]=2; count[2]=count[1]+count[2]=2+3=5; count[3]=count[3]+count[2]=1+5=6;
为了方便理解,我们把键索对应的字符显示出来:

然后就是排序了,构建一个辅助数组aux[]。
从a[0]逐一排序:
因为a[0]=d,d对应的键索为3,count[3]=6,故aux[6]=d, count[3]+=1;

因为a[1]=a,a对应的键索为0,count[0]=0,故aux[0]=a, count[0]+=1;
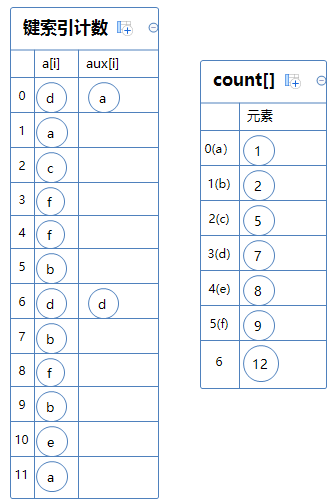
因为a[2]=c,c对应的键索为2,count[2]=5,故aux[5]=c, count[2]+=1;
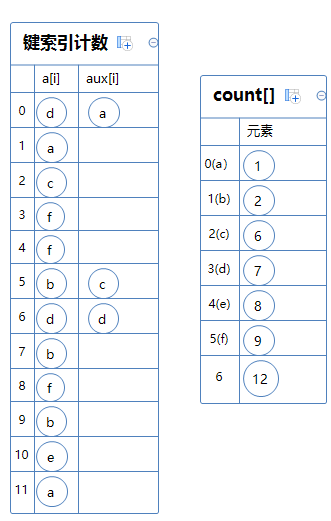
因为a[3]=f,f对应的键索为5,count[5]=9,故aux[9]=f, count[5]+=1;

如此类推,直到aux[]填满了。

aux[]就是排序完毕后的数组,最后只需把aux[]复制给a[]即可,算法结束。
总结一下通用思路就是:
令a[]是拥有一堆只有一个字符的string数组,且有R个不同的字符。
1. 创建一个int类型的拥有R+1个元素的数组count和一个与a[]同等大小的string数组aux[];
2. 数这些不同的字符分别重复出现了多少次,并把次数记录在count[x+1]中。x为某个字符对应的键索;
3. 计算比某个字符小的字符有多少个,计算方法为count[x+1] += count[x]。x为某个字符对应的键索。(x从0开始逐渐递增)
4. 通过利用count[]把a[]的元素逐一添加到aux[]中
5. 把aux[]复制给a[]
键索引计数法是稳定的(Stable),如果不了解稳定是什么意思,继续往下看,稍后将介绍。
代码实现:

4. LSD基数排序(LSD radix sort )
现在开始讲String排序算法。
LSD全称:Least-significant-digit-first 低位有效数字优先。
如果要排序的那堆字符串长度相同,我们可以用LSD基数排序。
从例子入手:a[]是拥有一堆只有三个字符的string数组。
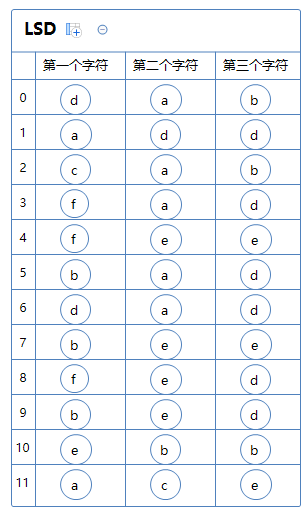
为了方便理解,我把这些字符都特意分开标示出来了。a[0]=dab;a[1]=add;a[2]=cab; ...
首先,我们先对第三个字符那一列通过键索引计数法把这堆字符串排一次序:

理所当然的,因为这些字符串每个都是一个个体,排序的时候,要整个字符串一起移动而不是只移动第三个字符。
标红的那一列已经排好序了。
接下来对第二个字符那一列通过键索引计数法把这堆字符串排一次序:
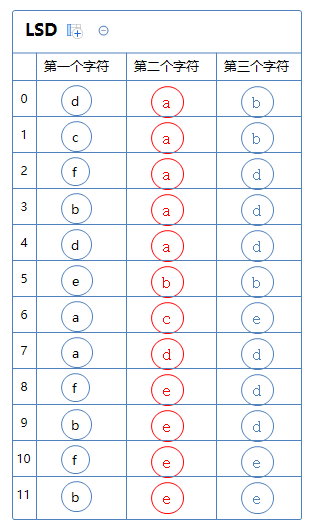
接下来对第一个字符那一列通过键索引计数法把这堆字符串排一次序:
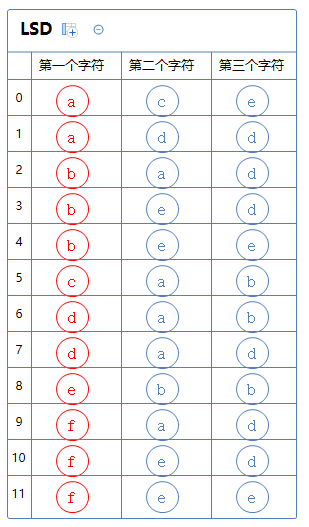
排序完成,算法结束。
稳定性问题:
在这里,我们可以讨论一下稳定性的问题了(stable)。我们经常说这个算法是稳定的(stable),那个算法是不稳定的(not stable)。
这里的稳定不是指可不可靠,而是指这个算法会不会破坏原有的顺序。
例如,我们看一下这个例子,经历了对第二个字符那一列通过键索引计数法把这堆字符串排一次序后,a[1]=cab; a[2]=fad。
它们在对第三个字符那一列通过键索引计数法把这堆字符串排一次序的那时,对应的位置在哪?a[1]=cab; a[4]=fad。
第一次排序时,cab在fad前面,因为它们的第三个字符b<d; 但第二次排序时,这两个字符串的第二个字符都是a,不稳定的算法有可能会把fad排到cab前面,但稳定的算法肯定不会!
总结一下LSD基数排序通用思路就是:
如果需要排序的那堆字符串拥有一样多的字符,那么我们可以从它们的最后一个字符进行键索引计数法排序,然后对它们的倒数第二个字符进行键索引计数法排序,如此类推,直到对它们的第一个字符进行键索引计数法排序后,排序结束。
键索问题:
但是,键索引计数法是需要知道要排序的字符串有多少个不同的字符的,从而给那些字符匹配键索,难道我们每次都要去数一下有多少个不同的字符?
其实并不需要,这样做太耗费时间了。看下表:

根据每个不同类型的字符串,我们可以选择不同的R值(键索引计数法构建count数组需要用到的R值)。
如果我们知道要排序的字符串都是由小写字母组成,则R=26(毕竟只有26个字母);
如果要排序的字符串还有一些符号,那就用R=256吧。
总之,按照需求选择R值。
LSD基数排序的代码实现:

5. MSD基数排序(MSD radix sort )
那么如果要排序的那堆字符串长度不同,怎么办?那就用MSD基数排序吧!
MSD全称:Most-significant-digit-first 高位有效数字优先。
LSD是从最后一位字符开始往前排序的,而MSD是从第一位字符开始往后排序的。
从例子入手:a[]是拥有一堆字符串的字符串数组。

为了方便理解,我把这些字符都特意分开标示出来了。a[0]=she;a[1]=sells;a[2]=seashells; ...
我们设定每个字符串的最后一位字符的下一个位置的空字符的键索为-1,即:(为了方便观察,这里将暂时标红它们)
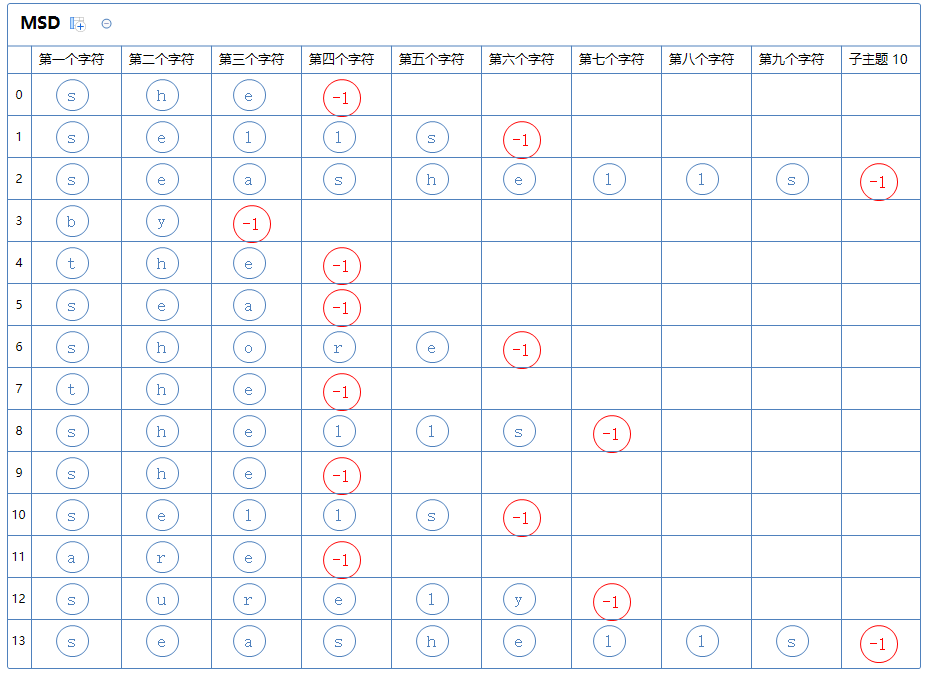
每次进行键索引计数法排序时,我们都按照排序结果,把所有字符串分成数个区。如下:
首先,我们先对第一个字符那一列通过键索引计数法把这堆字符串排一次序:
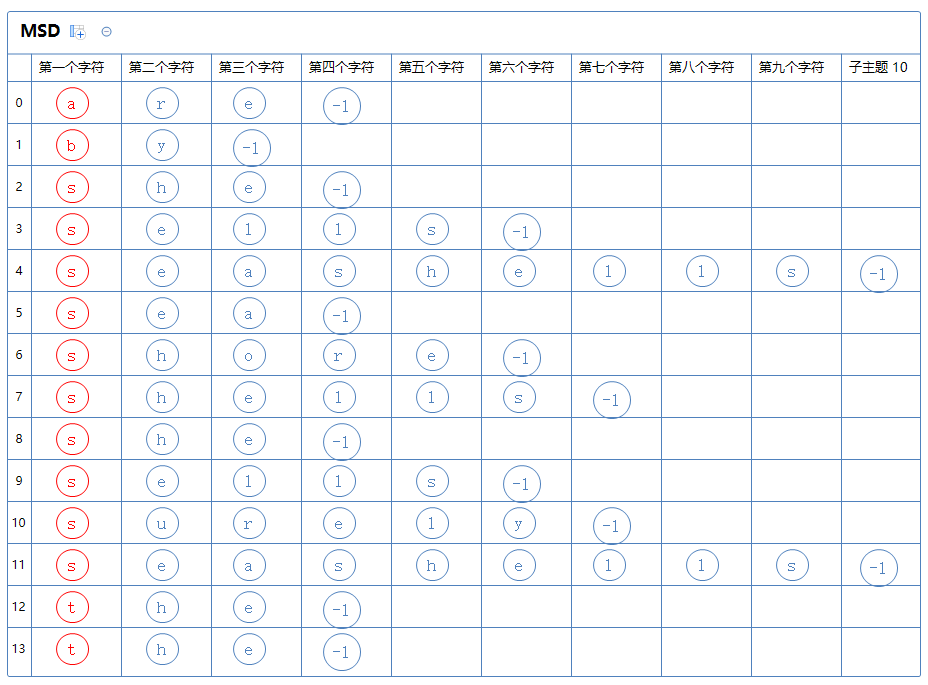
第一个字符那一列只有4个不同的字母,故把所有字符串分为4个区:
第一个区有a[0];第二个区有a[1];第三个区有a[2]~a[11];第四个区有a[12]、a[13]。
然后从上往下看:
第一个区只有一个字符串,此区排序完毕;
第二个区只有一个字符串,此区排序完毕;
第三个区有很多个字符串,对此区的第二个字符那一列通过键索引计数法把这堆字符串排一次序:(为了方便观察,已排序完毕的字符串用绿色表示)

继续分区:
第一个区有a[2]~a[6];第二个区有a[7]~a[10];第三个区有a[11]。
然后从上往下看:
第一个区有很多个字符串,对此区的第三个字符那一列通过键索引计数法把这堆字符串排一次序:(为了方便观察,待排序的字符串用黑色表示)

继续分区:
第一个区有a[2]~a[4];第二个区有a[5]、a[6]。
然后从上往下看:
第一个区有很多个字符串,对此区的第四个字符那一列通过键索引计数法把这堆字符串排一次序:
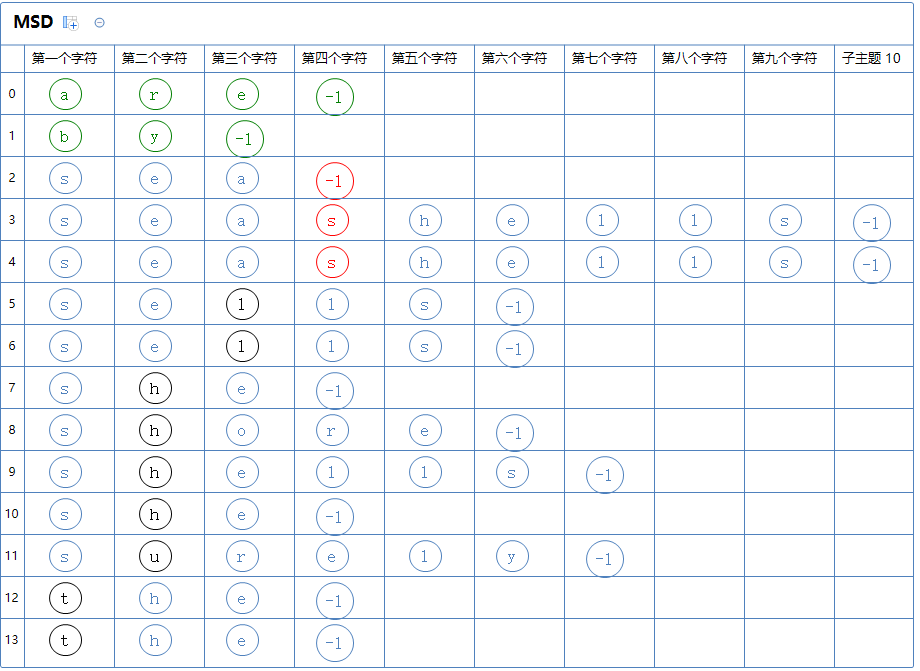
在这次排序中,-1的效果就能表现出来了:因为分配键索时,字符分到的键索都是正数,这里的-1是最小的,故这样可以保证最短的字符在最前面。
继续分区:只有一个区,此区有a[3]、a[4]。(-1不是字符,不参与分区)
此区有很多个字符串,对此区的第五个字符那一列通过键索引计数法把这堆字符串排一次序:

继续分区:只有一个区,此区有a[3]、a[4]。
此区有很多个字符串,对此区的第六个字符那一列通过键索引计数法把这堆字符串排一次序:
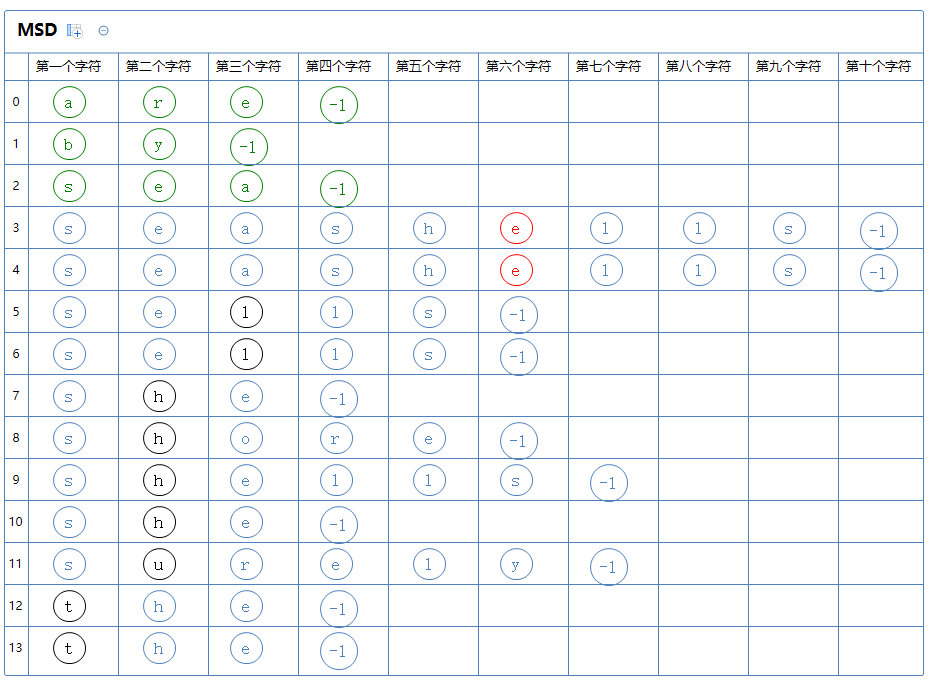
(由于这两个字符串是相同的,故每次排序后的结果都一样,这里省略第7、8个字符的排序)
继续分区:只有一个区,此区有a[3]、a[4]。
此区有很多个字符串,对此区的第九个字符那一列通过键索引计数法把这堆字符串排一次序:

继续分区:只有一个区,此区有a[3]、a[4]。
此区有很多个字符串,对此区的第十个字符那一列通过键索引计数法把这堆字符串排一次序:
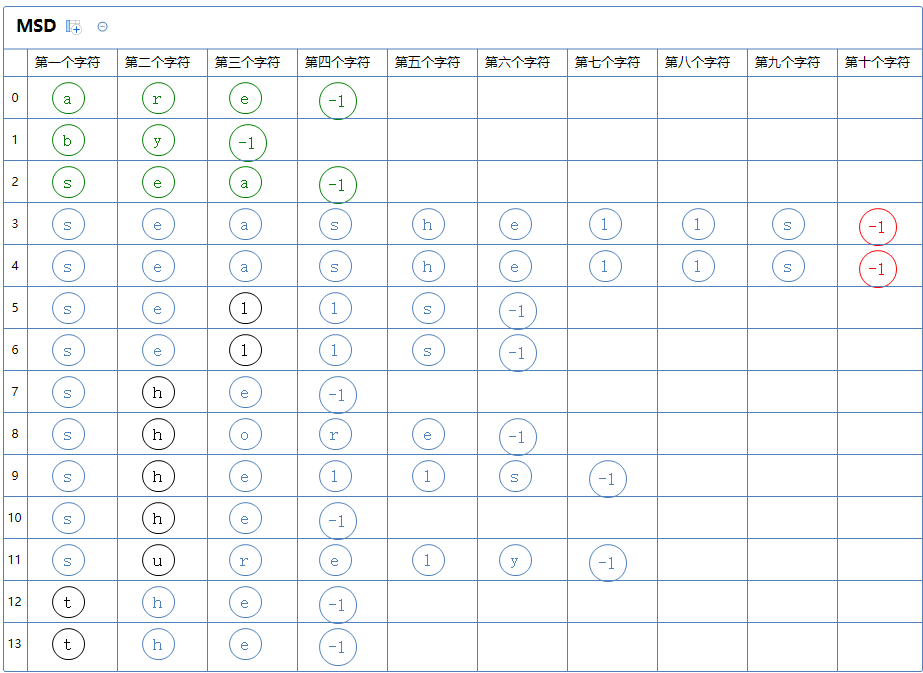
继续分区:没有区(因为都是-1,-1不是字符,不参与分区)
此区排序完毕,开始下一个区的排序:
此区有很多个字符串,对此区的第四个字符那一列通过键索引计数法把这堆字符串排一次序:
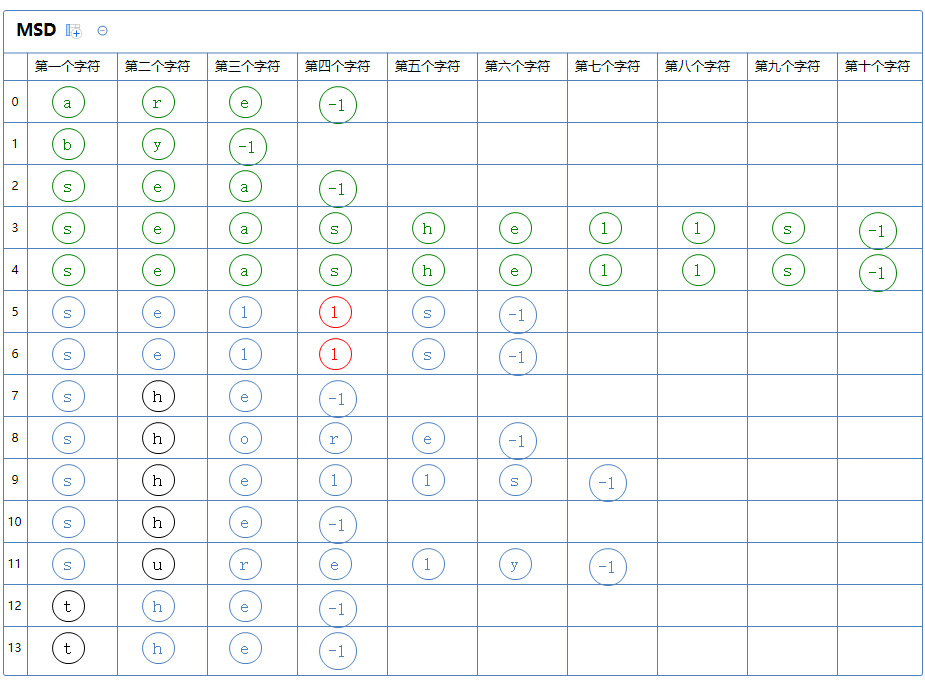
继续分区:只有一个区,此区有a[5]、a[6]。
此区有很多个字符串,对此区的第五个字符那一列通过键索引计数法把这堆字符串排一次序:
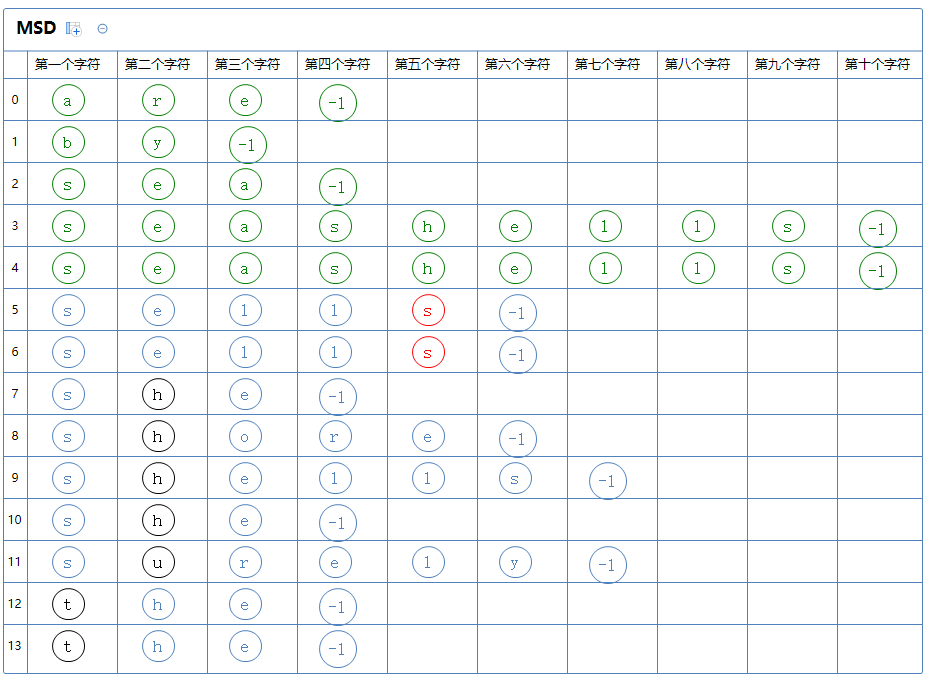
继续分区:只有一个区,此区有a[5]、a[6]。
此区有很多个字符串,对此区的第六个字符那一列通过键索引计数法把这堆字符串排一次序:
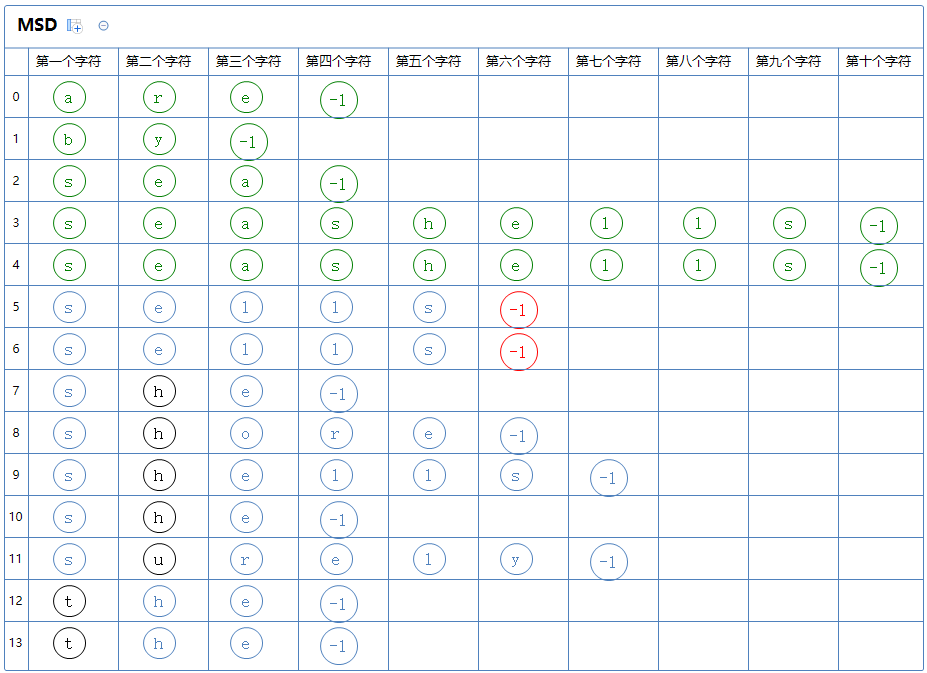
继续分区:没有区(因为都是-1,-1不是字符,不参与分区)
此区排序完毕,开始下一个区的排序:
此区有很多个字符串,对此区的第三个字符那一列通过键索引计数法把这堆字符串排一次序:
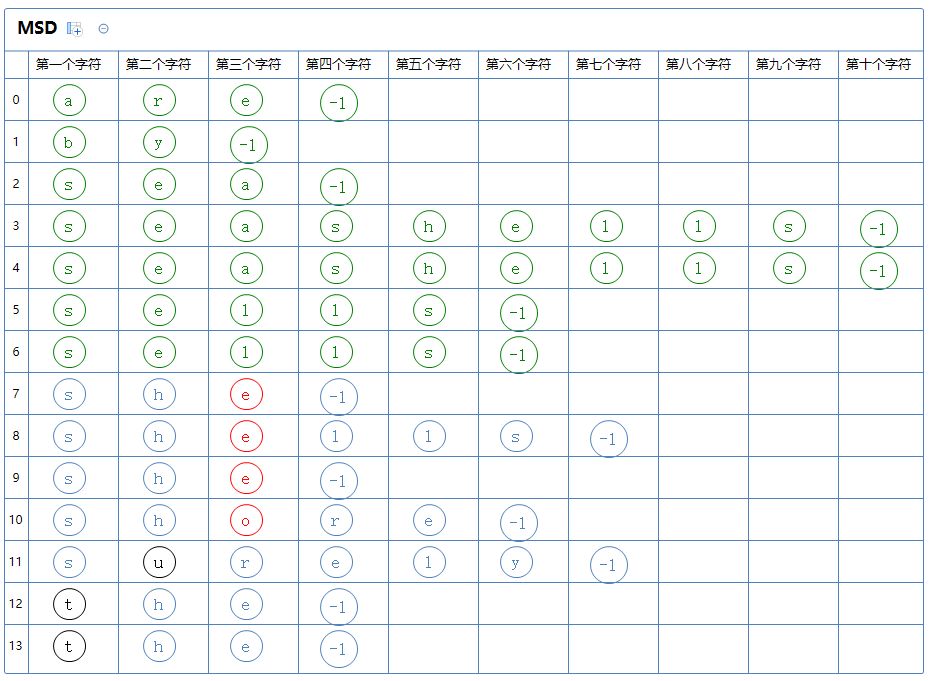
继续分区:
第一个区有a[7]~a[9];第二个区有a[10]。
然后从上往下看:
第一个区有很多个字符串,对此区的第四个字符那一列通过键索引计数法把这堆字符串排一次序:

继续分区:只有一个区,此区有a[8]。(-1不是字符,不参与分区)
此区只有一个字符串,此区排序完毕。
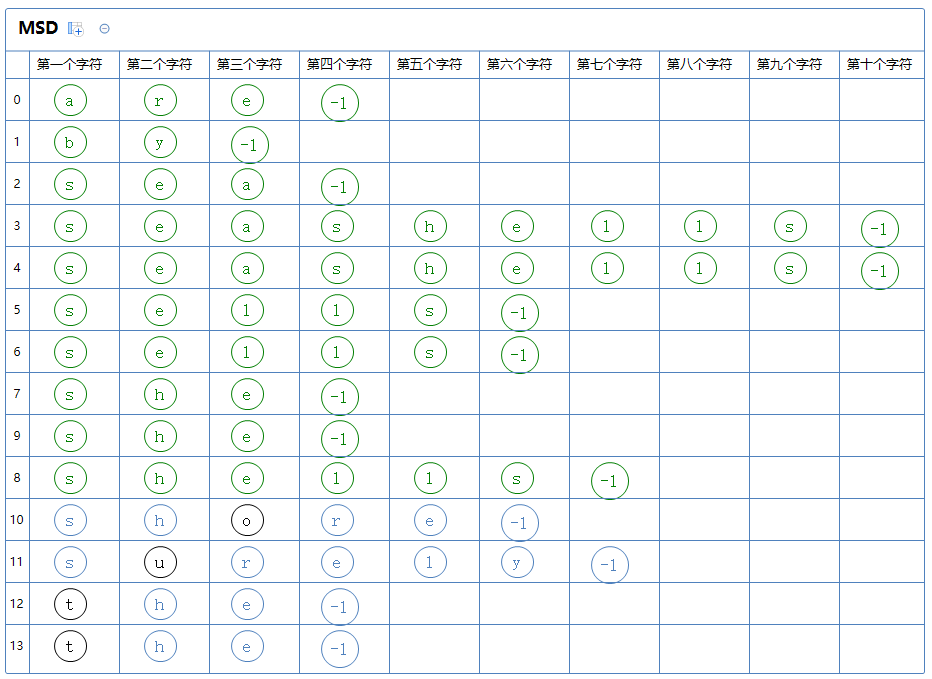
开始下一个区的排序:
此区只有一个字符串,此区排序完毕。
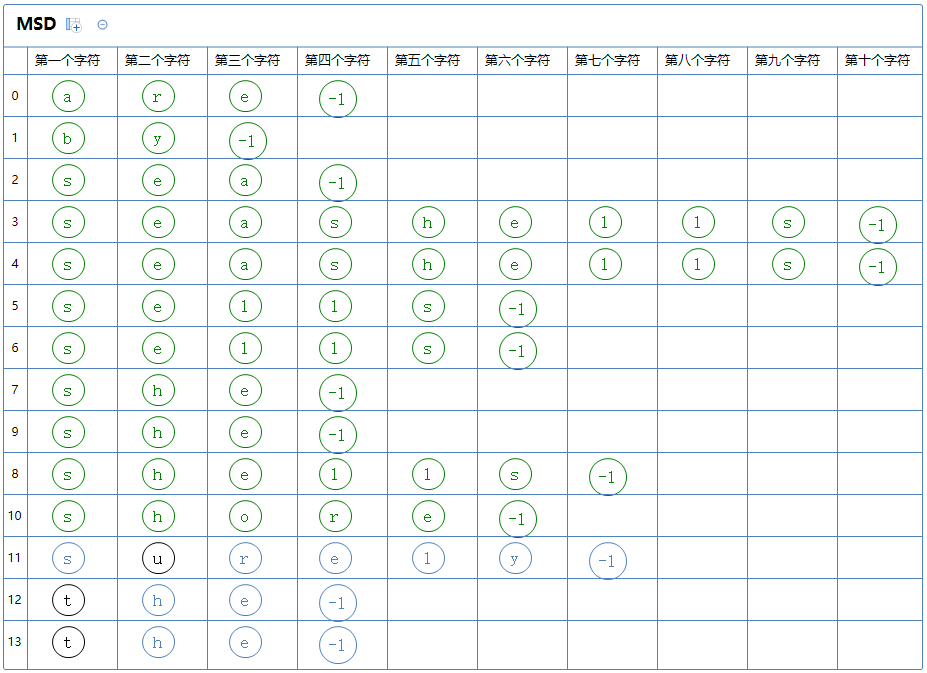
开始下一个区的排序:
此区只有一个字符串,此区排序完毕。

开始下一个区的排序:
此区有两个字符串,但由于它们是一样的,故这里省略对此区的第二、第三、第四个字符那一列分别通过键索引计数法排序:

没有下一个区了,全部排序完毕,算法结束。
这个算法演示过程本身就是一个递归的过程。
总结一下:
1. 对所有字符串的第一个字符那一列通过键索引计数法把这堆字符串排一次序,根据排序结果进行分区;
2. 从上往下处理各个分区:如果分区只有一个字符串,则此区处理完毕;如果有多个字符串,则对此区的字符串的下一个字符进行排序、分区、处理分区。
3. 所有分区处理完后,排序完毕,算法结束。
实现代码:
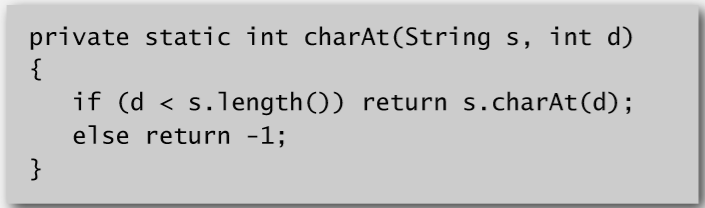
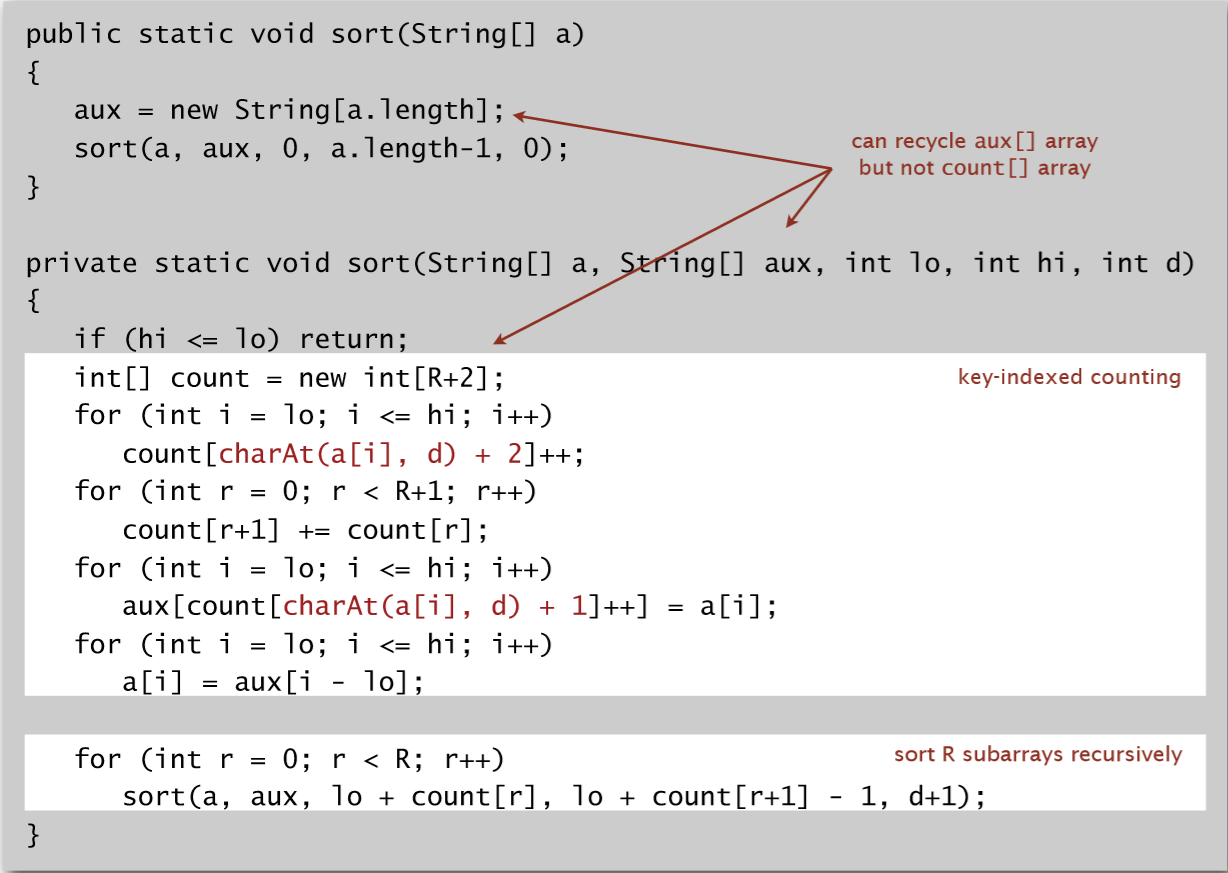
6. LSD和MSD的算法效率
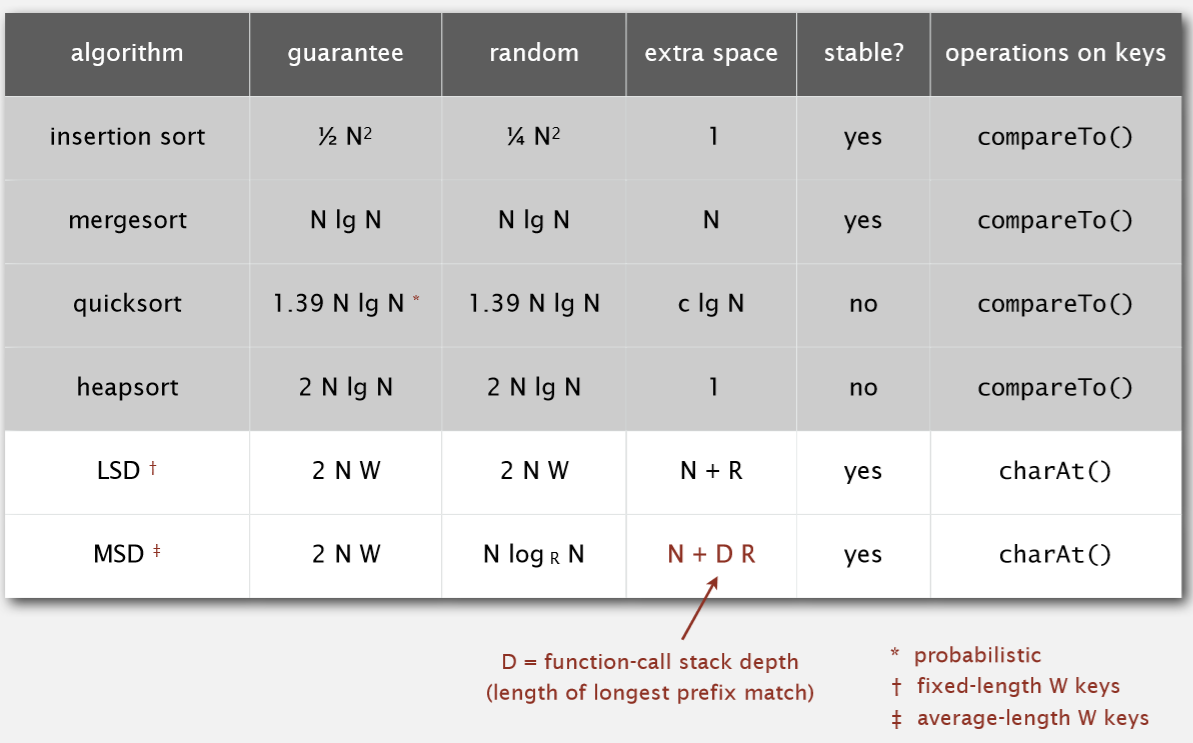
注释:
N为要排序的元素个数。
LSD的W: 由于LSD只针对于要排序的那堆字符串长度相同,故W为字符串的长度。
MSD的W: 要排序的那堆字符串的长度平均值。
guarantee: 算法保证能在多少次操作后完成。
random: 如果要排序的数组里的元素顺序是随机的,则算法可以在多少次操作后完成。
extra space: 算法需要的额外空间。
7. MSD算法的缺陷
1. MSD算法需要额外空间(键索引计数法每次排序都需要使用额外空间),这意味着浪费内存。
2. 递归循环里的每次循环都需要进行很多操作。
在字符串算法—字符串排序(下篇)中,将把MSD算法和快速排序法结合起来,形成更高效率的算法: 3区基数快速排序(3-way radix quicksort)。
另外,如果我们需要在一篇文章中搜索关键词,如何高效地操作?
在字符串算法—字符串排序(下篇)中,我们将介绍后缀排序法( suffix sort )来解决搜索关键词的问题。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号