1. 什么是最短路径(Shortest Path)
对于一个有向图(不了解有向图的,建议先看一下有向图),如果它的所有边都带有一定的数值(即带权),则会变成下面的样子
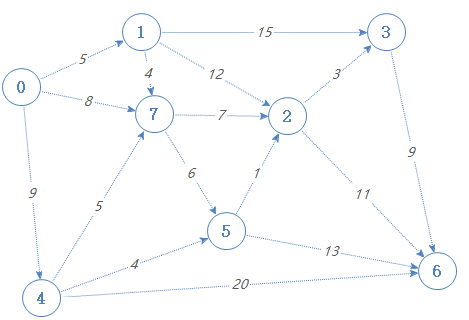
如果我们在点5,想去点6,应该怎么走最快?显然5-2-6这条路最短。这就是点5到点6的最短路径。
给定一个点,求这个点到所有其它点的最短路径。这就是本篇算法要解决的问题。
如果学会了本篇算法,那么去做一个导航系统也不难了。
2. 生成带权的有向图
因为这种有向图只比普通有向图多了些权值,我们只需在每条边上多加一个变量来记录权值即可。
使用的邻接列表也需要把权值信息写上,如下图:
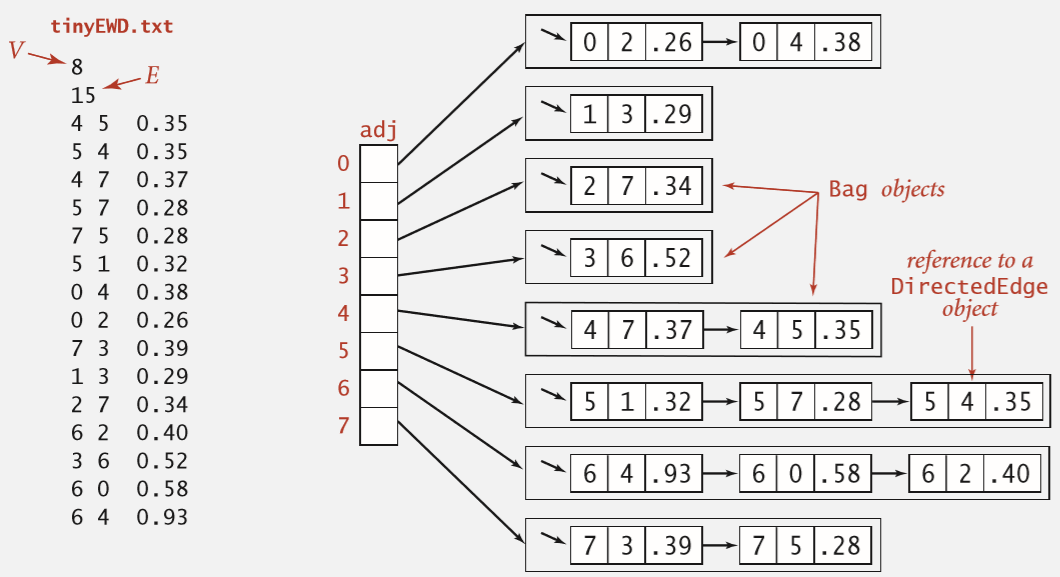
针对不同情况,本文将介绍3种解决最短路径的算法。
3. 迪杰斯特拉算法(Dijkstra's algorithm)
这个算法要求这个有向图没有拥有负权值的边。
从例子入手:

我们需要创建几个数组:
创建一个边的数组EdgeTo,记录某个点是从哪个点来的;
创建一个double类型的数组DistTo,记录从给定点到某个点的距离;
创建一个点的数组Points。
假设给定的点为点0。
把点0加入Points中。
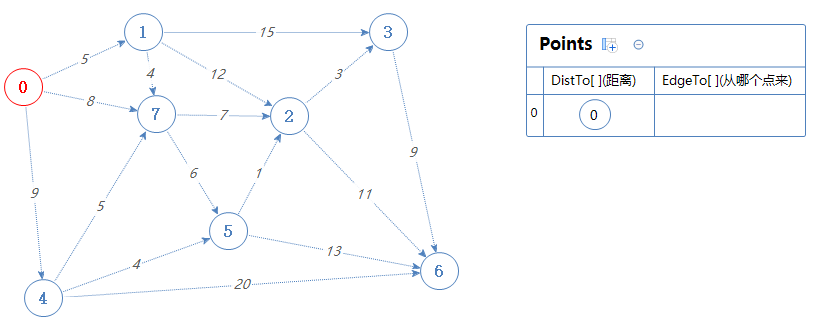
DistTo[0]=0的意思是从点0到点0的距离为0。
然后Points输出并移除一个最小值:0。(为方便理解,移除用标红来表示)
把0可以去的点(1,7,4)加入到Points中。
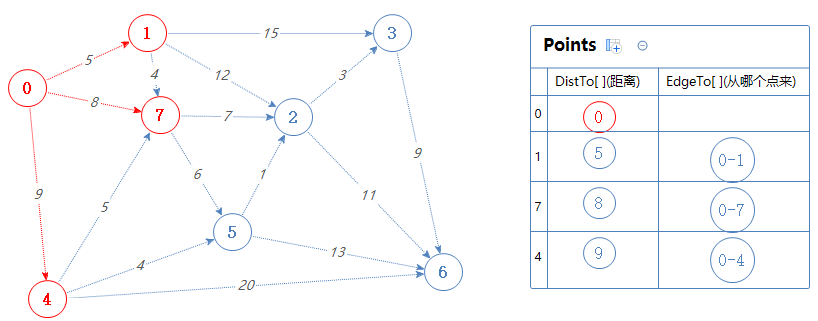
EdgeTo[1]=0的意思是点1是从点0来的。
然后Points输出并移除一个最小值:1。
把1可以去的点(3,2,7)加入到Points中,但7已经在Points里了,0-1-7的总权值为5+4=9,比Points里面的7对应的距离大,故无视之。

然后Points输出并移除一个最小值:7。
把7可以去的点(2,5)加入到Points中,但2已经在Points里了,0-7-2的总权值为8+7=15,比Points里面的2对应的距离小,故取代之。
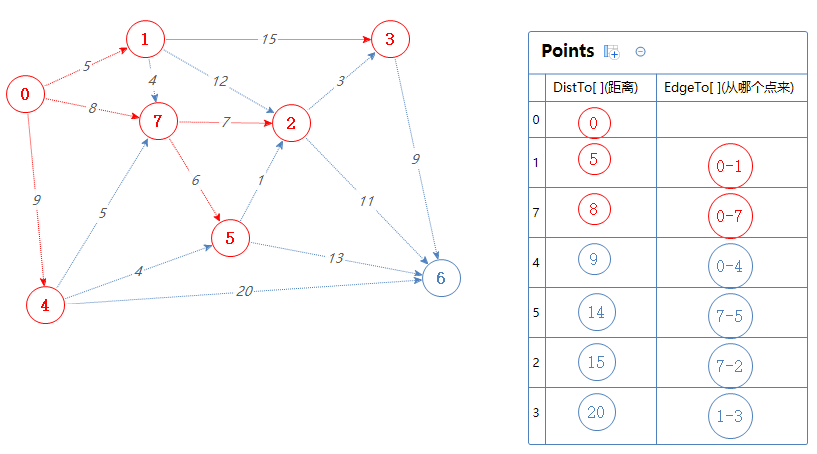
然后Points输出并移除一个最小值:4。
把4可以去的点(7,5,6)加入到Points中,但7,5已经在Points里了,0-4-7的总权值为9+5=14,比Points里面的7对应的距离大,故无视之;
0-4-5的总权值为9+4=13,比Points里面的5对应的距离小,故取代之;
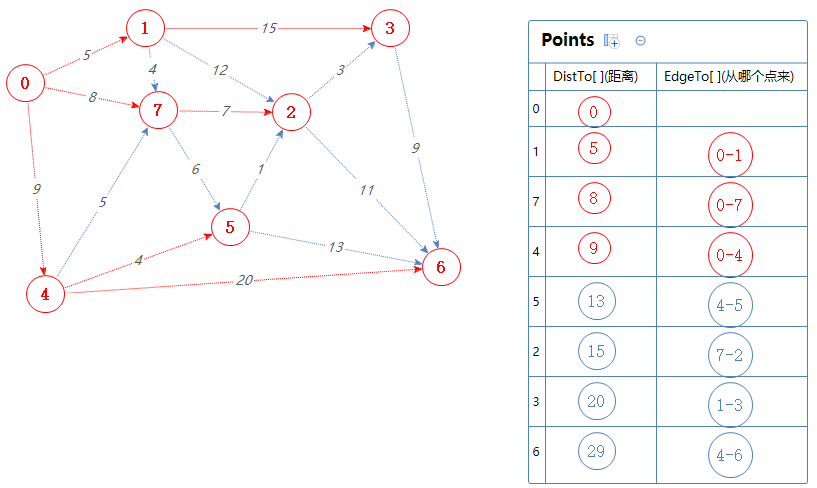
然后Points输出并移除一个最小值:5。
把5可以去的点(2,6)加入到Points中,但2,6已经在Points里了,0-4-5-2的总权值为9+4+1=14,比Points里面的2对应的距离小,故取代之;
0-4-5-6的总权值为9+4+13=26,比Points里面的6对应的距离小,故取代之;

然后Points输出并移除一个最小值:2。
把2可以去的点(3,6)加入到Points中,但3,6已经在Points里了,0-4-5-2-3的总权值为9+4+1+3=17,比Points里面的3对应的距离小,故取代之;
0-4-5-2-6的总权值为9+4+1+11=25,比Points里面的6对应的距离小,故取代之;
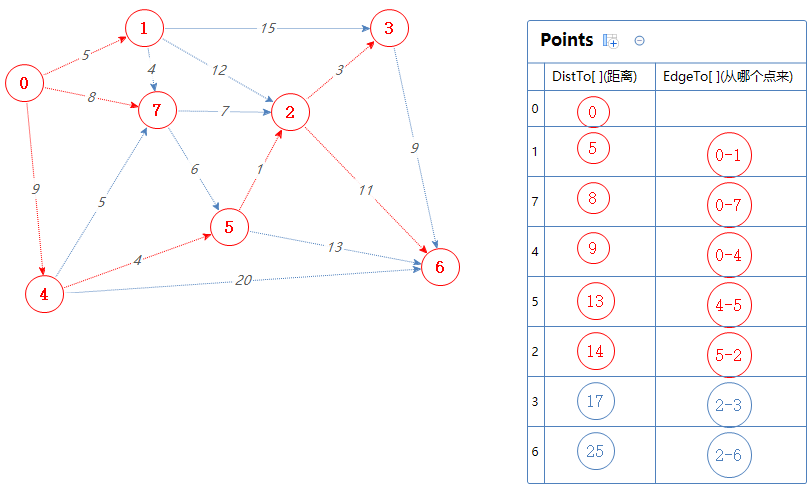
然后Points输出并移除一个最小值:3。
把3可以去的点(6)加入到Points中,但3已经在Points里了,0-4-5-2-3-6的总权值为9+4+1+3+9=26,比Points里面的6对应的距离大,故无视之。
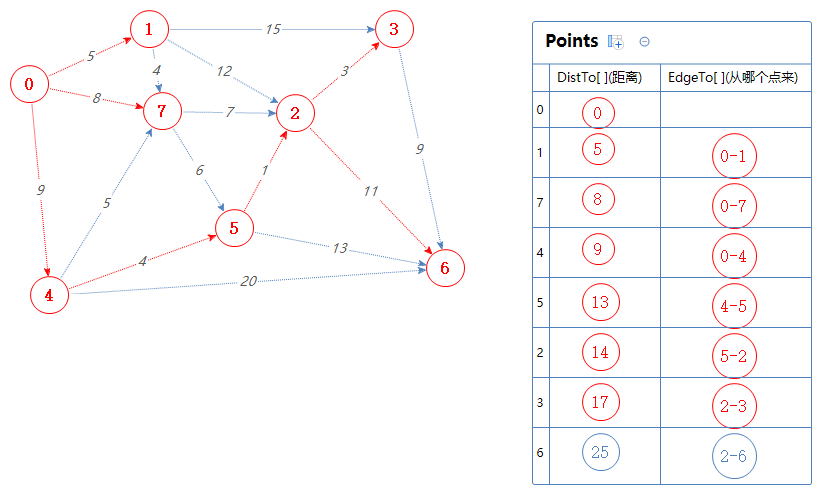
然后Points输出并移除一个最小值:6。
6没有可去的点,Points里没有元素了,最短路径全部找完,结束算法。
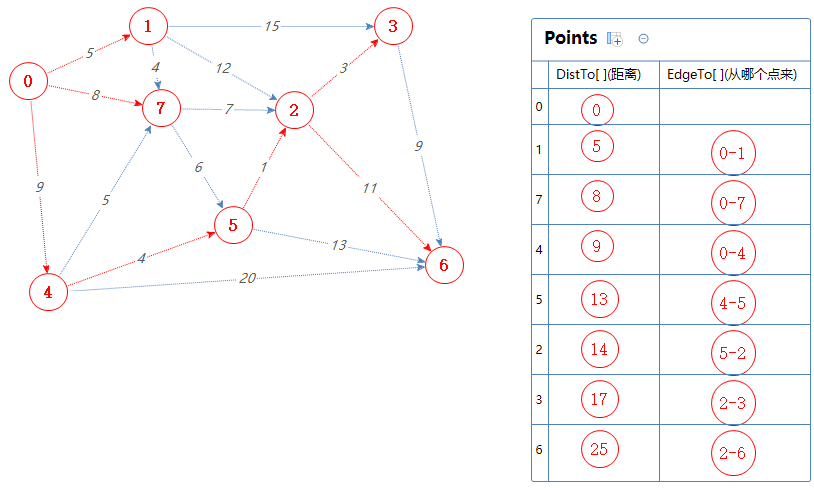
总结一下通用思路就是:
1. 把给定的点加入Points中
2. Points输出并移除一个拥有最小距离的点a
3. 把点a能去的点全部加进Points里,如果有重复,则比较新加进来的和原有的路线哪个短,哪个短取哪个
4. 重复2,3步直到Points没有元素为止
第二步中的从数组输出一个最小值,建议用最小堆来实现,这样会比较高效。
实现代码:
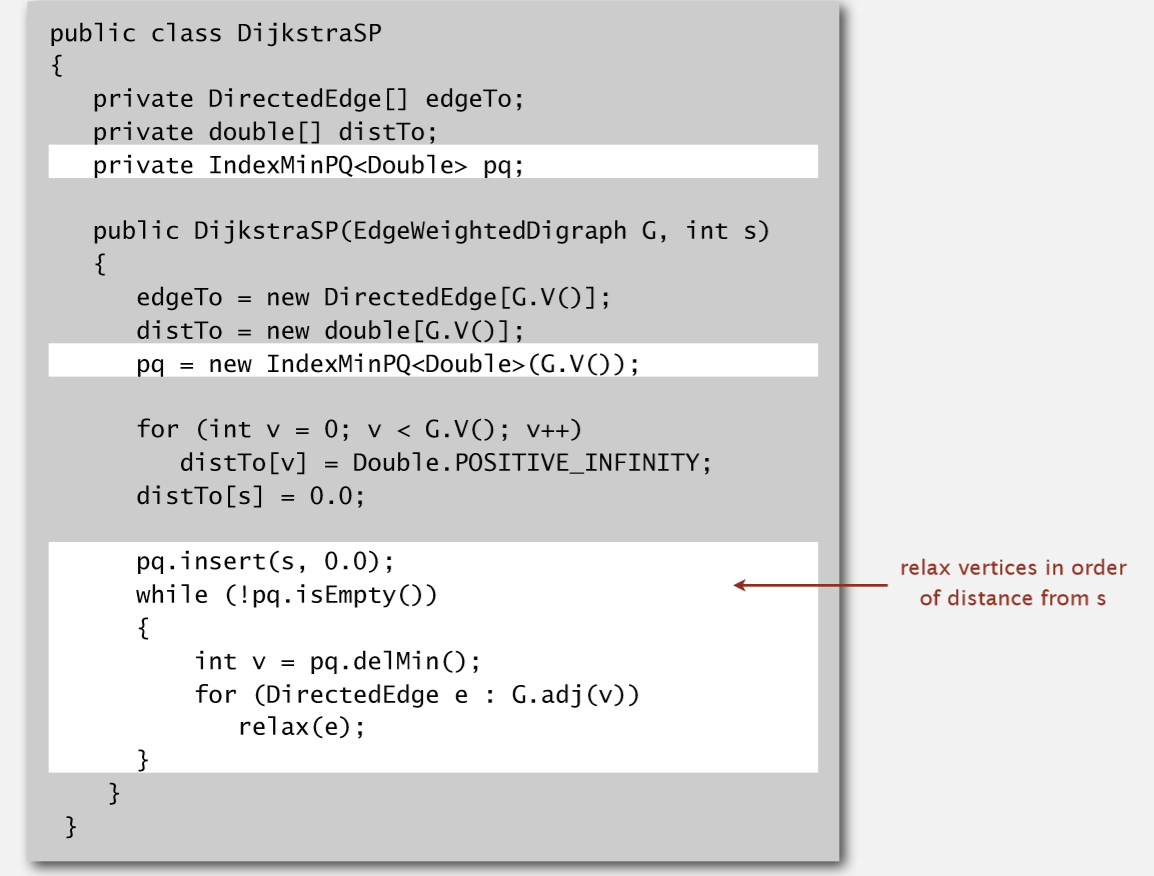
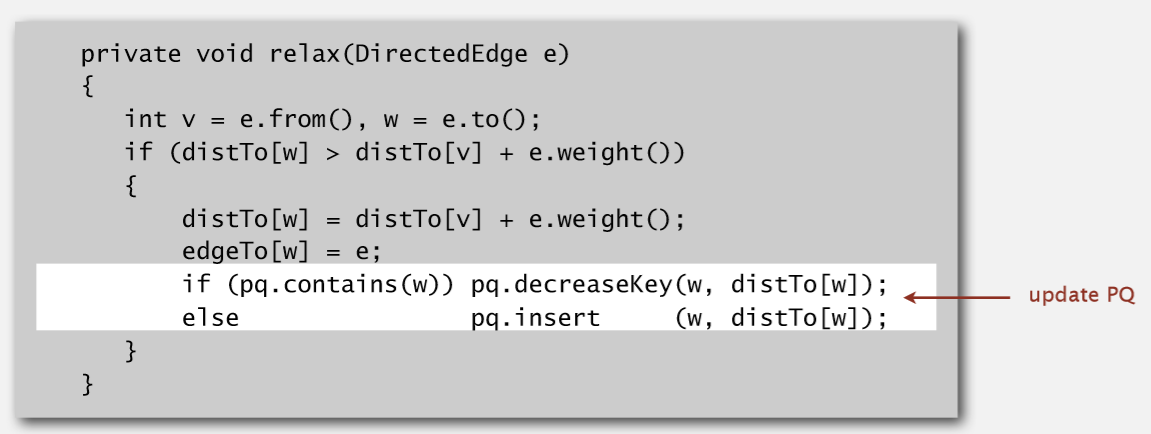
4. 用拓扑序列求最短路径
如果要求最短路径的有向图是有向无环图,那么有种算法比迪杰斯特拉算法(Dijkstra's algorithm)快,那就是用拓扑序列求最短路径。(如果不了解有向图的拓扑序列,建议先看一下有向图。)
从例子入手:

我们需要创建几个数组:
创建一个边的数组EdgeTo,记录某个点是从哪个点来的;
创建一个double类型的数组DistTo,记录从给定点到某个点的距离;
创建一个点的数组Points。
假设给定的点为点0.
进行拓扑排序后得到拓扑序列S:0 4 1 7 5 2 3 6。 (注意,这个拓扑序列不唯一,也有可能是 0 1 4 7 5 2 3 6,对最短路径结果不影响)
根据拓扑序列S,第一个点是点0,把0加入Points中。
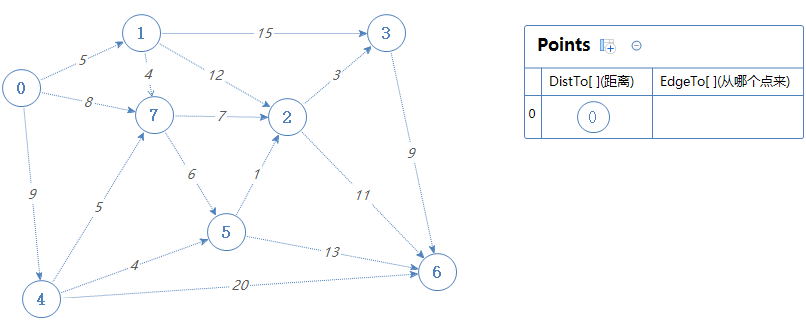
把0可以去的点(1,7,4)加入到Points中。

根据拓扑序列S:0 4 1 7 5 2 3 6
下一个点为4。
把4可以去的点(7,5,6)加入到Points中。但7已经在Points里了,0-4-7的总权值为9+5=14,比Points里面的7对应的距离大,故无视之;
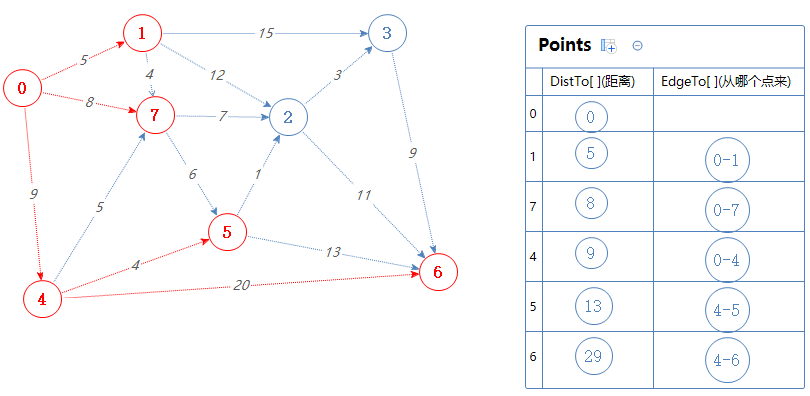
根据拓扑序列S:0 4 1 7 5 2 3 6
下一个点为1。
把1可以去的点(3,2,7)加入到Points中,但7已经在Points里了,0-1-7的总权值为5+4=9,比Points里面的7对应的距离大,故无视之。
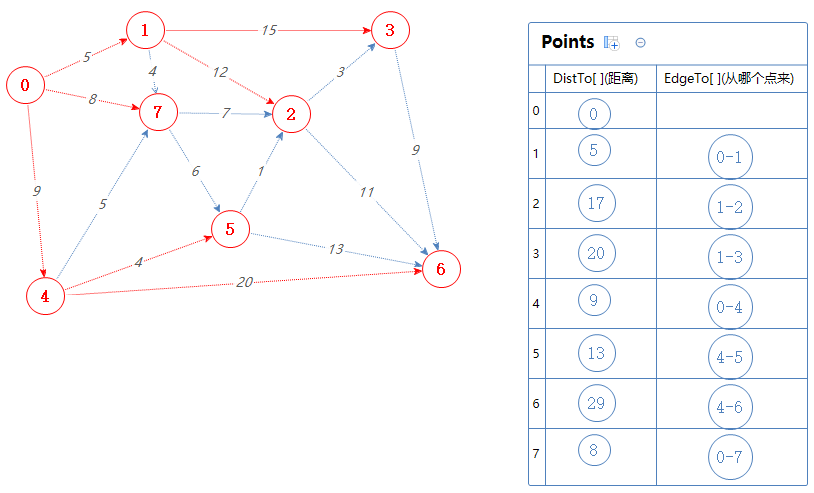
根据拓扑序列S:0 4 1 7 5 2 3 6
下一个点为7。
把7可以去的点(2,5)加入到Points中,但2,5已经在Points里了,0-7-2的总权值为8+7=15,比Points里面的2对应的距离小,故取代之。
0-7-5的总权值为8+6=14,比Points里面的2对应的距离大,故无视之。
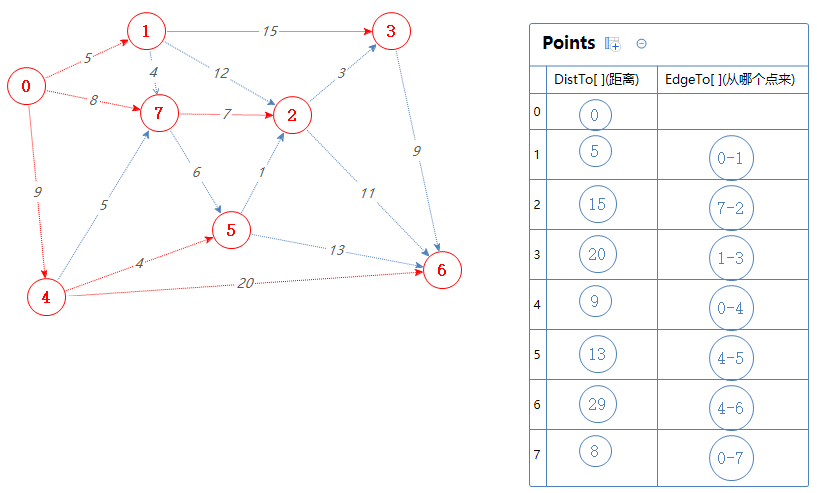
根据拓扑序列S:0 4 1 7 5 2 3 6
下一个点为5。
把5可以去的点(2,6)加入到Points中,但2,6已经在Points里了,0-4-5-2的总权值为9+4+1=14,比Points里面的2对应的距离小,故取代之;
0-4-5-6的总权值为9+4+13=26,比Points里面的6对应的距离小,故取代之;
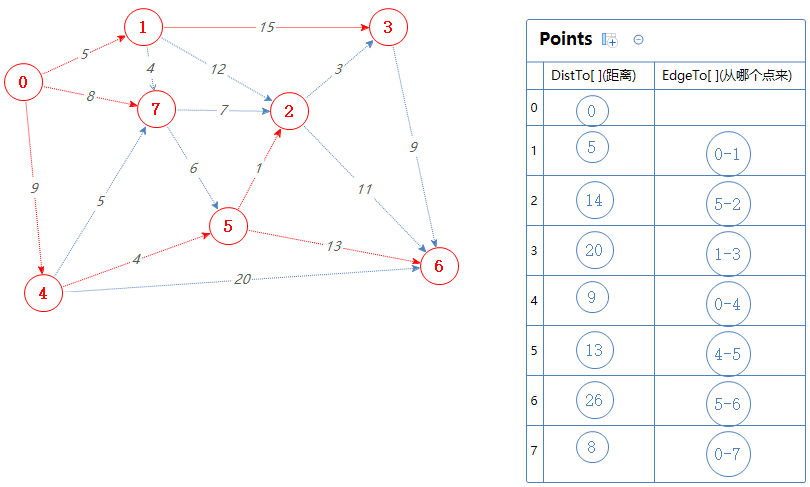
根据拓扑序列S:0 4 1 7 5 2 3 6
下一个点为2。
把2可以去的点(3,6)加入到Points中,但3,6已经在Points里了,0-4-5-2-3的总权值为9+4+1+3=17,比Points里面的3对应的距离小,故取代之;
0-4-5-2-6的总权值为9+4+1+11=25,比Points里面的6对应的距离小,故取代之;
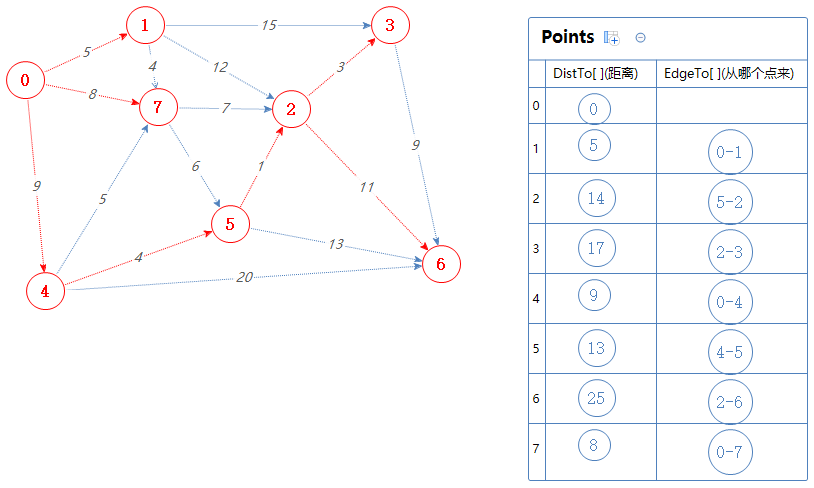
根据拓扑序列S:0 4 1 7 5 2 3 6
下一个点为3。
把3可以去的点(6)加入到Points中,但3已经在Points里了,0-4-5-2-3-6的总权值为9+4+1+3+9=26,比Points里面的6对应的距离大,故无视之。
根据拓扑序列S:0 4 1 7 5 2 3 6
下一个点为6。
6没有可去的点。
拓扑序列S数完,最短路径全部找完,结束算法。
与迪杰斯特拉算法(Dijkstra's algorithm)相比,这个算法省去了V次(V为这个有向图的总点数)寻找最小值的过程,多了一个拓扑排序的过程,因此效率更高。
但是,同样地,这个算法也要求这个有向图没有拥有负权值的边。
总结一下通用思路就是:
1. 按给定的点对有向无环图进行拓扑排序,得到拓扑序列S
2. 根据拓扑序列S的顺序逐一输出点a
3. 把点a能去的点全部加进Points里,如果有重复,则比较新加进来的和原有的路线哪个短,哪个短取哪个
4. 重复2,3步直到拓扑序列S输出完为止
代码实现:
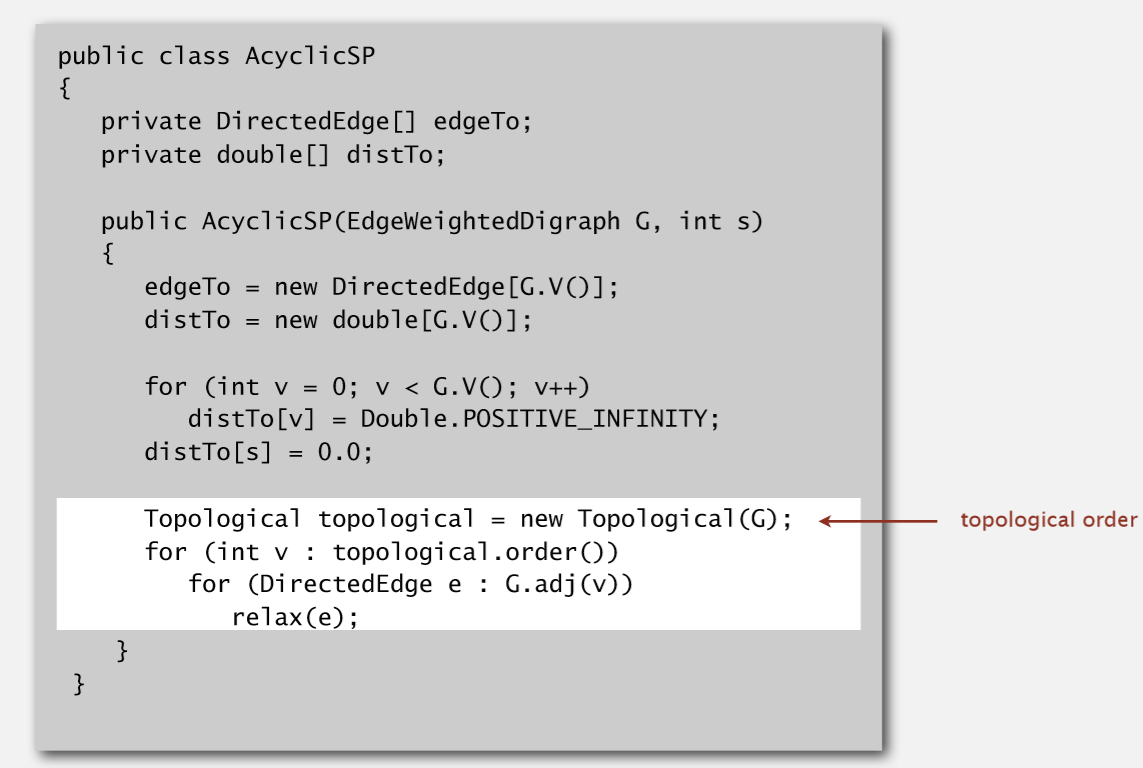
5. 贝尔曼-福特算法(Bellman-Ford algorithm)
如果这个有向图有拥有负权值的边时,最短路径怎么求?这个算法可以解决,但效率上会比上述两个算法低。
在介绍这个算法前,先讨论一种情况:
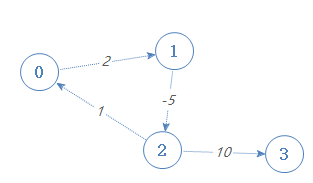
这个是有有向有环图(有内部循环),且这个内部循环权值总和为负值(1+2-5=-2)。
那么0到3的最短路径是什么呢?
0-1-2-3 总权值为7
0-1-2-0-1-2-3 总权值为5
0-1-2-0-1-2-0-1-2-3 总权值为3
只要我们走一次负的内部循环,总路径权值就会减2,那么我们一直走就会一直减下去。所以,有负的内部循环存在时,求最短路径是没意义的。
接下来,我们讨论的是没负的内部循环情况。开始介绍算法:
从例子入手:(注意,我们这个例子有两个拥有负权值的边)
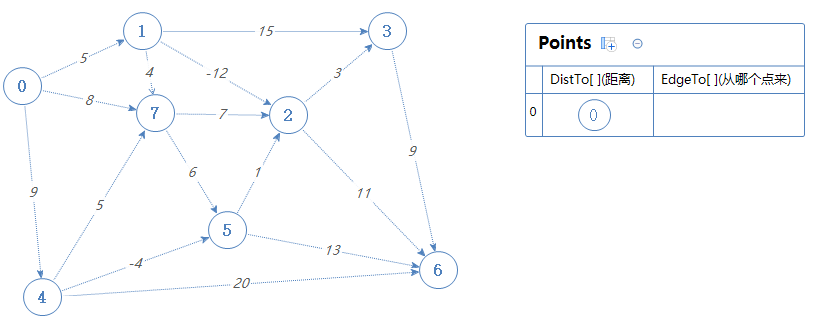
我们需要创建几个数组:
创建一个边的数组EdgeTo,记录某个点是从哪个点来的;
创建一个double类型的数组DistTo,记录从给定点到某个点的距离;
创建一个点的数组Points。
假设给定的点为点5.
则对于点5来说,DistTo[5]=0; 对于其他点来说,DistTo[其他点]=无限远。为什么要设定为无限远下面会讲到。
我们将根据0,1,2,3,4,5,6,7的顺序依次遍历所有边,然后重复这个操作V-1次(V为这个有向图的总点数)。
把所有点加入到Points内。
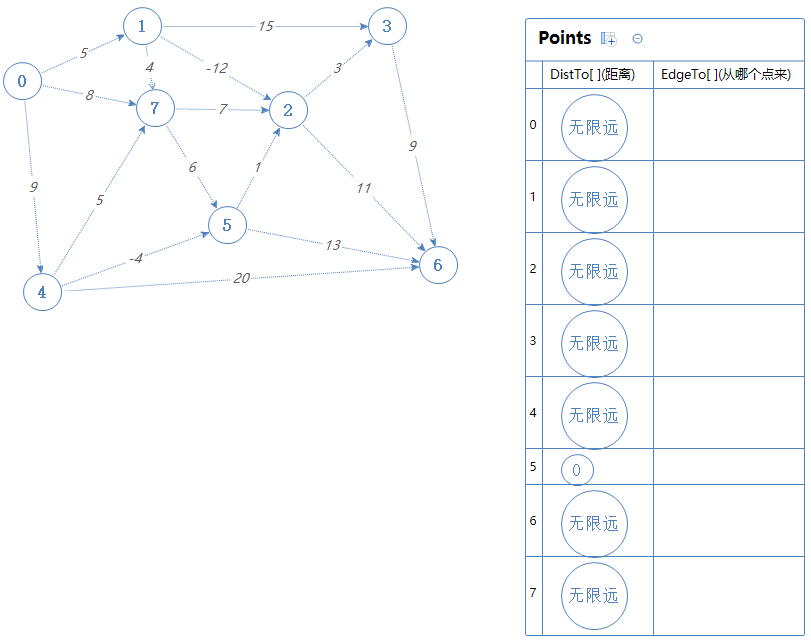
把0可以去的点(1,7,4)加入到Points中。但1,7,4都已经在Points里了,由于0的距离为无限远,所以新加入的点全部无视。
把1可以去的点(2,7,3)加入到Points中。但2,7,3都已经在Points里了,由于1的距离为无限远,所以新加入的点全部无视。
把2可以去的点(6,3)加入到Points中。但6,3都已经在Points里了,由于2的距离为无限远,所以新加入的点全部无视。
把3可以去的点(6)加入到Points中。但6都已经在Points里了,由于3的距离为无限远,所以新加入的点全部无视。
把4可以去的点(5,7,6)加入到Points中。但5,7,6都已经在Points里了,由于4的距离为无限远,所以新加入的点全部无视。

然后把5可以去的点(2,6)加入到Points中。但2,6都已经在Points里了,5-2的总权值为1,比Points里面的2对应的距离小,故取代之;
5-6的总权值为13,比Points里面的6对应的距离小,故取代之;

然后6无路可去。
第一遍结束,接下来开始第二遍。(总共要6遍!)
把0可以去的点(1,7,4)加入到Points中。但1,7,4都已经在Points里了,由于0的距离为无限远,所以新加入的点全部无视。
把1可以去的点(2,7,3)加入到Points中。但2,7,3都已经在Points里了,由于1的距离为无限远,所以新加入的点全部无视。
把2可以去的点(6,3)加入到Points中。但6,3都已经在Points里了,5-2-3的总权值为4,比Points里面的3对应的距离小,故取代之;
5-2-6的总权值为12,比Points里面的3对应的距离小,故取代之;
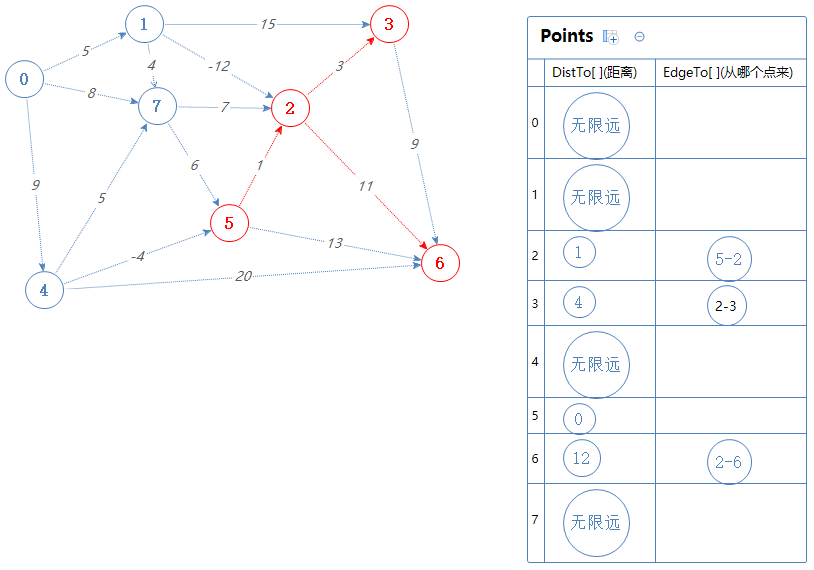
把3可以去的点(6)加入到Points中。但6都已经在Points里了,5-2-3-6的总权值为13,比Points里面的3对应的距离大,故无视之。
把4可以去的点(5,7,6)加入到Points中。但5,7,6都已经在Points里了,由于4的距离为无限远,所以新加入的点全部无视。
把5可以去的点(2,6)加入到Points中。但2,6都已经在Points里了,5-2的总权值为1,等于Points里面的2对应的距离,故无视之;
5-6的总权值为13,大于Points里面的6对应的距离,故无视之;
6无路可去。
第二遍结束,接下来应该开始第三、四、五、六遍,但结果都跟现在的一样,不重复累赘。
在这里应该可以感受到无限远的意义了:有些点例如0,1,4,7,根本没办法从5那里去到,所以对于点5来说,这些点是处于无限远的地方的。
如果我们输入寻找A点到B点的最短路径的指令时,程序返回的结果是无限远,我们应该能反应过来:A点没办法抵达B点。
从这个例子中可以看出,后面开始的第三、四、五、六遍纯属是浪费时间,这里是有可以优化的空间的:使用队列。感兴趣的可以去这里看一下。
总结一下通用思路就是:
1. 把给定点S的距离设为0,其它点的距离设为无限远
2. 按照递增的顺序把所有点能去的所有点全部加进Points里,如果有重复,则比较新加进来的和原有的路线哪个短,哪个短取哪个
3. 重复第2步V-1次(V为这个有向图的总点数),后算法结束。
PS:第二步是不是递增顺序都没所谓,只要保证能遍历所有点就好。
代码实现:(代码来自这:https://www.cnblogs.com/lxt1105/p/6478108.html)
#include <stdio.h> #include <stdlib.h> #define INFINITY 99999 //struct for the edges of the graph struct Edge { int u; //start vertex of the edge int v; //end vertex of the edge int w; //weight of the edge (u,v) }; //Graph - it consists of edges struct Graph { int V; //total number of vertices in the graph int E; //total number of edges in the graph struct Edge *edge; //array of edges }; void bellmanford(struct Graph *g, int source); void display(int arr[], int size); int main(void) { //create graph struct Graph *g = (struct Graph*)malloc(sizeof(struct Graph)); g->V = 4; //total vertices g->E = 5; //total edges //array of edges for graph g->edge = (struct Edge*)malloc(g->E * sizeof(struct Edge)); //------- adding the edges of the graph /* edge(u, v) where u = start vertex of the edge (u,v) v = end vertex of the edge (u,v) w is the weight of the edge (u,v) */ //edge 0 --> 1 g->edge[0].u = 0; g->edge[0].v = 1; g->edge[0].w = 5; //edge 0 --> 2 g->edge[1].u = 0; g->edge[1].v = 2; g->edge[1].w = 4; //edge 1 --> 3 g->edge[2].u = 1; g->edge[2].v = 3; g->edge[2].w = 3; //edge 2 --> 1 g->edge[3].u = 2; g->edge[3].v = 1; g->edge[3].w = -6; //edge 3 --> 2 g->edge[4].u = 3; g->edge[4].v = 2; g->edge[4].w = 2; bellmanford(g, 0); //0 is the source vertex return 0; } void bellmanford(struct Graph *g, int source) { //variables int i, j, u, v, w; //total vertex in the graph g int tV = g->V; //total edge in the graph g int tE = g->E; //distance array //size equal to the number of vertices of the graph g int d[tV]; //predecessor array //size equal to the number of vertices of the graph g int p[tV]; //step 1: fill the distance array and predecessor array for (i = 0; i < tV; i++) { d[i] = INFINITY; p[i] = 0; } //mark the source vertex d[source] = 0; //step 2: relax edges |V| - 1 times for(i = 1; i <= tV-1; i++) { for(j = 0; j < tE; j++) { //get the edge data u = g->edge[j].u; v = g->edge[j].v; w = g->edge[j].w; if(d[u] != INFINITY && d[v] > d[u] + w) { d[v] = d[u] + w; p[v] = u; } } } //step 3: detect negative cycle //if value changes then we have a negative cycle in the graph //and we cannot find the shortest distances for(i = 0; i < tE; i++) { u = g->edge[i].u; v = g->edge[i].v; w = g->edge[i].w; if(d[u] != INFINITY && d[v] > d[u] + w) { printf("Negative weight cycle detected!\n"); return; } } //No negative weight cycle found! //print the distance and predecessor array printf("Distance array: "); display(d, tV); printf("Predecessor array: "); display(p, tV); } void display(int arr[], int size) { int i; for(i = 0; i < size; i ++) { printf("%d ", arr[i]); } printf("\n"); }
6. 算法效率
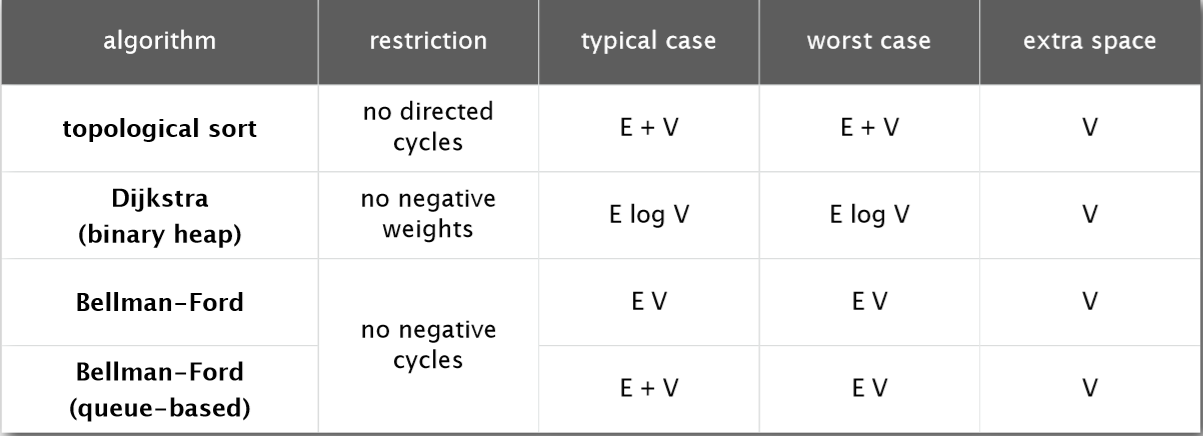
图中的E为有向图的总边数;V为有向图的总点数。
图中的迪杰斯特拉算法(Dijkstra's algorithm)是经过使用二叉堆优化的;图中贝尔曼-福特算法(Bellman-Ford algorithm)的queue-based是使用了队列优化。
用拓扑序列求最短路径要求有向图无内部循环,没拥有负权值的边;迪杰斯特拉算法(Dijkstra's algorithm)要求有向图没拥有负权值的边;贝尔曼-福特算法(Bellman-Ford algorithm)要求没总权值为负的内部循环。
PS: 贝尔曼-福特算法(Bellman-Ford algorithm)可以侦测到总权值为负的内部循环的存在。
图中logV=log2V。
一般情况下,用拓扑序列求最短路径算法效率最高,迪杰斯特拉算法(Dijkstra's algorithm)其次,贝尔曼-福特算法(Bellman-Ford algorithm)最低。
但使用了队列优化后,贝尔曼-福特算法(Bellman-Ford algorithm)有可能比迪杰斯特拉算法(Dijkstra's algorithm)效率高。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步