万花筒模拟

背景介绍

还不知道什么是万花筒的小朋友请点击这里：

 最常见的万花筒，侧边是由三面镜子构成的，镜子不断反射底部的图像，产生千变万化的组合。它产生的图像比如：

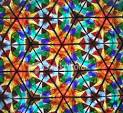 （图1）（图2）

为了更清晰的解释，我们用下面的图为例：

（图3）

以上图ABC为例 ，真实的图像是中间最亮的三角形部分，其余的镜像都是由镜子反射造成的。

我们的目标就是要用计算机模拟万花筒生成的图像。

目标详解

输入：

底图，以上面ABC为例，就是中间最亮的三角形部分；

输出：

以底图为基础，正确的绘制出反射图像。不仅要考虑最简单的平铺形式（ABC这个例子就是平铺）；还要考虑万花筒的镜子可以调整，比如调整后可以生成图2所示的结果。

具体目标：

-正确的处理图像镜像；

-模拟镜子的非理想表面，比如散射和反照率。

目标分析

•  处理图像镜像

有两个备选方案：

方法一，中心图像是原始图像，其它部分都是原始图像的镜像，很自然想到算出正确的镜像平铺开即可。基本原理如下图所示。

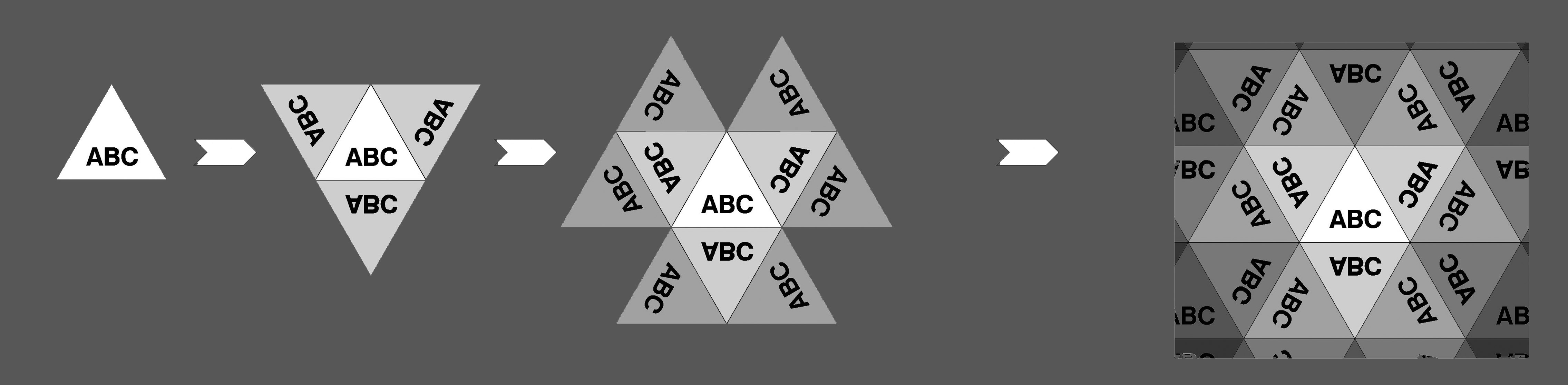
但是为了模拟更一般的情况（比如图2），镜像是在三维空间而不是二维空间中计算的。另外，要考虑到镜像之间交叉或者重叠情况。

除了以上这些问题，这个方法最重要的潜在的问题是：由于并非物理模拟，不容易扩展；比如镜子的材质或形状改变，很可能会导致这种方法的失效。

当然，这个方法的优点也很明显，就是效率，如果用GPU实现，几乎没有什么计算，除了简单的纹理采样计算。

考虑到我们的主要是用于实验目的，效率的要求不是特别迫切，我们尝试寻找更接近物理的模拟方法。

方法二，光线跟踪。不了解光线跟踪但感兴趣的同学请wiki之。

适合用光线跟踪的原因如下：接近物理真实情况；在万花筒有限的空间内，光线跟踪计算也比较简单。二维简化图示意如下：

 

• 模拟镜子的非理想表面

现实世界的镜子不是完美的，模拟的时候可以把这些“缺陷”也考虑进去。我想到两点：

一个是反照率(albedo)，我们需要在每一次反射的时候，乘以一个小于1的系数来实现。它产生的效果就是中间图像最亮，越往外图像越暗。

另外一个是漫反射，非理想镜子表面也存在漫反射。经过多次反射后，产生的效果是图像的模糊；反射次数越多，图像模糊度越大。ray trace的时候产生漫反射的光线可以解决这个问题，但是会使计算量按几何级数增加，这个计算量目前是无法负担的。最简单的模拟办法是通过mipmap来模拟，反射次数越多的地方采用尺寸越小的mipmap slice，当然这个方法并不精确，和实际效果是有偏差的。

• 在现实基础上的扩展

除了模拟现实，我们可以在我们创造的虚拟世界中加入现实中不存在的元素，或做各种奇怪的实验。

比如，镜子的面数可以改变，镜子之间的夹角可以随意改变。

比如，镜子可以有倾斜度（即和底面的夹角并非直角），图2就是一个实例。

比如，底面（即原始图平面）本身也可以倾斜。

比如，镜子反射光线的时候，可以使用抖动技术；这样反射次数多的地方，会产生溶解的效果。

确定方案

使用D3D在Pixel Shader中做ray trace的核心计算，充分利用GPU的并行计算能力；

在单独窗口中设置参数，不占用主界面的显示空间。

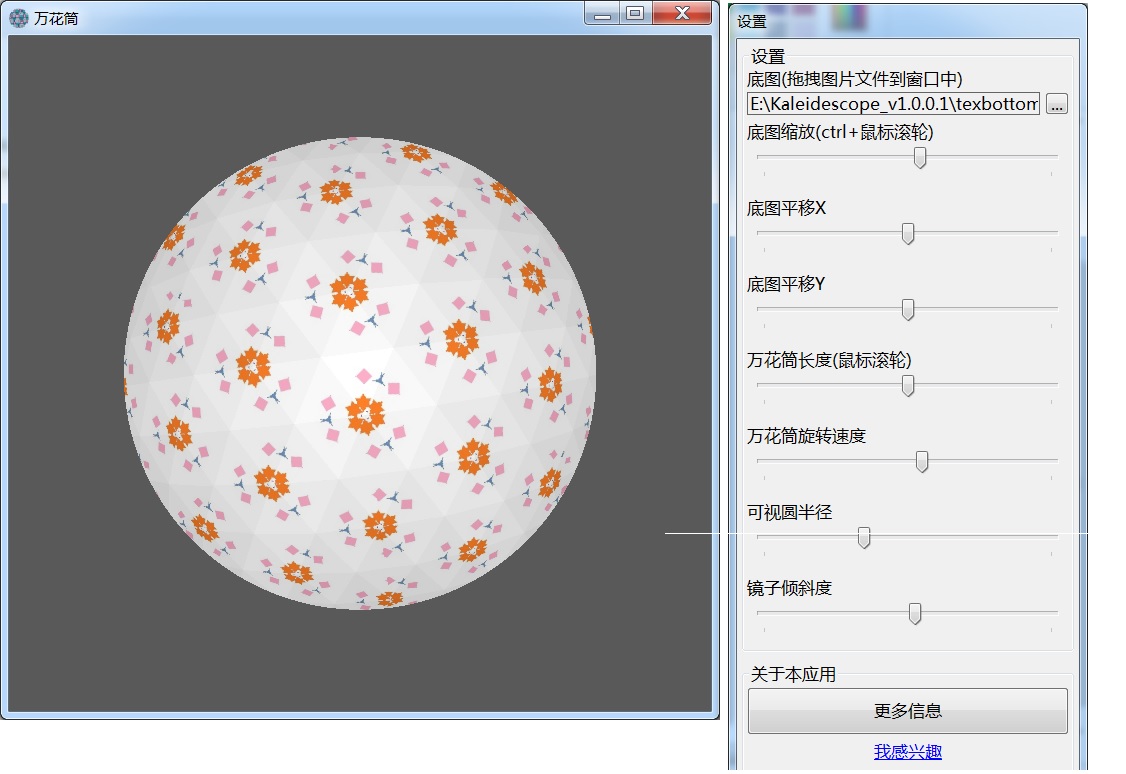
此版本结果展示

截图

下载地址

https://files.cnblogs.com/mchz/Kaleidescope_v1.0.0.1.rar

运行环境要求

WinXP SP2 or Higher
DirectX11 Runtime & DirectX10 Supported Video Card
VS2012 Runtime(https://files.cnblogs.com/mchz/vcredist_x86.rar)

功能详述

----------
|V1.0.0.1|
----------
第一个版本。本应用的目的是模拟万花筒。核心功能通过D3D在GPU上实现。
此版本实现的功能有：
支持三面镜子，且三面镜子组成一个柱体或台体，剖面是正三角形（这也是现实中绝大多数万花筒的实现方式）。
可调节的参数是：
-设置底图: 底图指的是万花筒底部的实际物体（比如多彩碎屑），我们用图片文件模拟，支持拖拽图片到窗口;
-支持底图缩放;
-支持底图平移;
-万花筒长度调节: 长度越长，底面离眼睛越远，镜子越长;
-万花筒旋转速度调节;
-可视圆半径: 指的是圆形Mask的半径。半径越小，在GPU上执行速度越快;
-可调节镜子倾斜度: 这样三面镜子可组成台体（顶部和底部剖面大小不同）而不是一般的柱体。