Day3练习赛
题目目录
第一题 切瓜
题意
一个球形的西瓜,切$n$刀,请问最多能切成几块?答案对$10^9+7$取模。
$n\leq 10^9$。
题解
啊啊啊,我们可以求出 $n=1,2,3,4$ 时的解,然后猜想答案的公式是(因为是三维的)
$$ans=an^3+bn^2+cn+d$$
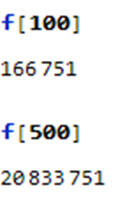
然后,把我们求出的解带到Mathematica里算一下——
啊哈!然后我们的猜测就变成了
$$ans=\frac{n^3+5n+6}{6}$$
然后我们代一下样例:
真不错!正确了。
但是。。$n^3$要高精度啊。
这里,我们有两种选择:使用逆元或者分解因式。
我们来试一下分解因式:
哦!不会爆炸了!
或者,我们求出 $6$ 在 $10^9+7$ 下的逆元,然后直接 $\mathbin{\mathrm{mod}}$ 做。
附上代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#ifdef _WIN32
#define LL "%I64d"
#else
#define LL "%lld"
#endif
#define Daiwohao(x) (ans *= ((x) % 1000000007)) %= 1000000007;
ll rd() { char ch; ll ret=0; bool nag=false;while(!isdigit(ch=getchar()))nag|=ch=='-';ret=ch-'0';while(isdigit(ch=getchar()))ret=ret*10+ch-'0';return nag?-ret:ret;}
int main() {
for (int i=0; i<5; i++) {
ll n = rd();
ll w6 = 166666668, ans=1;
Daiwohao(n+1)
Daiwohao(n*n-n+6)
Daiwohao(w6)
printf(LL "\n", ans);
}
return 0;
}第二题 糕
等待填补。。。
第三题 倒水游戏
先鸽着