2018NOIP第四次膜你赛

传送门

第一题 我们爱几何

题意

给定$n$个整点$x_i,y_i$。从中挑出$k\geq 3$个点组成一个多边形。求有没有一种挑点的方式使得该多边形为正多边形_{注：每条边和每个夹角都相等的多边形叫做正多边形}。

$n\leq 1000,-10^9\leq x_i,y_i\leq 10^9$。

题解

好难啊

后来听大佬说，再看几遍题目。然后就看到了那个

整点

嗯。那整点又有什么用处呢？

丢结论跑：由整点构成的多边形只能是正四边形（正方形）。

为什么？引用一下大佬的话：

证明： 首先证明大于4的整点正多边形不存在。 反证假设正k(k>4)边形存在，对于多变形上的一个点i和i在逆时针方向的后继j，将i绕j顺时针转90°可以得到一个新点i'，可知i'也是整点。 于是可以对每个点都得到一个新点，可知k个新点也组成了一个更小的正k边形，由于整点多边形面积不能无限小，故与假设矛盾。 证明整点正三角形不存在留作作业好了，也很简单。

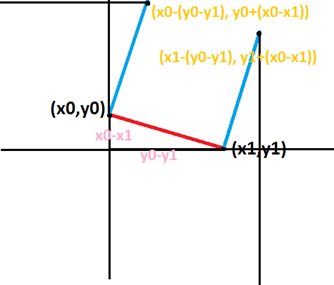
啊啊啊。那么我们枚举两个点$(x_1,y_1)$和$(x_2,y_2)$，然后连接它们——

真不错！那么，我们可以枚举下面红色的那条线，然后算出上面黄色的两个点！

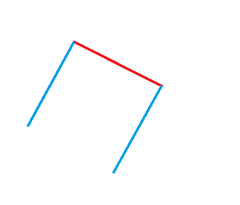
当然，还有一种情况：

同理，我们也可以算出下面的两个点。

然后，我们二分或者哈希或者STL的set(不要用map，我超时了，改成set就对了)，就可以通过此题啦！

上代码：

#include <bits/stdc++.h>
using namespace std;

struct node {
	int x,y;
	node(int x, int y) : x(x), y(y) {}
	bool operator < (const node & res) const {
		return x == res.x ? y < res.y : x < res.x;
	}
};
#define finish { ok=true; goto finished; }
set<node> S;
vector<node> A;
inline int rd() { int ret; scanf("%d", &ret); return ret; }
inline bool _(const node & res) { return S.find(res) != S.end(); }

int main() {
	int T,n; scanf("%d", &T);
	while (T--) {
		scanf("%d", &n);
		S.clear(); A.clear();
		for (int i=1; i<=n; i++) {
			A.push_back(node(rd(), rd()));
			S.insert(*(--A.end()));
		}
		bool ok = false;
		for (int i=0; i<n; i++) {
			for (int j=i+1; j<n; j++) {
				int detx = A[i].x - A[j].x;
				int dety = A[i].y - A[j].y;
				if (_(node(A[i].x-dety, A[i].y+detx))
					&& _(node(A[j].x-dety, A[j].y+detx))) finish
				if (_(node(A[i].x+dety,A[i].y-detx))
					&& _(node(A[j].x+dety, A[j].y-detx))) finish
			}
		}
	finished:
		if (ok) puts("4");
		else puts("-1");
	}
	return 0;
}

第二题 我们爱数数

先坑着

第三题 我们爱序列

题意

$1\leq N,M,Q\leq 1000000,1\leq a,b,A_i\leq M$。

题解

一个非常正统的基础数据结构应用。 我们使用并查集，$n$个位置每个位置都建立一个节点，$m$种颜色也都建立一个节点。 对于初始的$A_x=y$，我们将位置x的节点的父亲设为颜色y的节点。 对于一次修改$(a,b)$，我们将颜色$a$的节点的父亲设为颜色$b$的节点，并对颜色$a$新建一个单节点。 对于最后的输出，对于每个位置只要求出它所在的并查集的根是代表的哪个颜色即可。 注意对于$a=b$的情况的处理。

附上抢最短用的代码：

t,n,m,q,a[1<<20],b[1<<20];p(int v){int x,y;scanf("%d%d",&x,&y);v<q?p(v+1):0;b[x]=b[y];}main(){scanf("%d%d%d",&n,&m,&q);for(t=1;t<=n;++t)scanf("%d",&a[t]);for(t=1;t<=m;++t)b[t]=t;p(1);for(t=1;t<=n;++t)printf("%d ",b[a[t]]);return 0;}