数据结构和算法系列12 五大查找之二叉排序树

这一篇开始总结的是二叉排序树。构造一棵二叉排序树的目的，其实并不是为了排序，而是为了提高查找和插入删除的效率。

那么什么是二叉排序树呢？二叉排序树具有以下几个特点。

1，若根节点有左子树，则左子树的所有节点都比根节点小。

2，若根节点有右子树，则右子树的所有节点都比根节点大。

3，根节点的左，右子树也分别为二叉排序树。

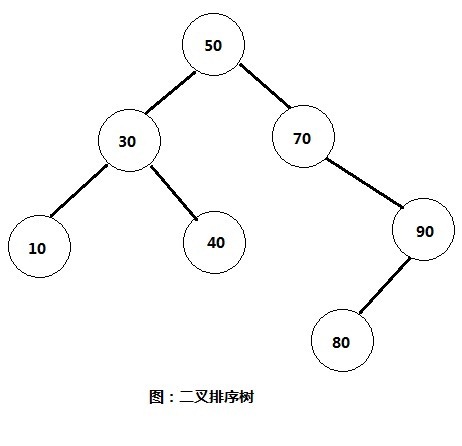
下面是二叉排序树的图示，通过图可以加深对二叉排序树的理解。

下面是二叉排序树常见的操作及思路。

1，插入节点

思路：比如我们要插入数字20到这棵二叉排序树中。那么步骤如下：

1) 首先将20与根节点进行比较，发现比根节点小，所以继续与根节点的左子树30比较。

2) 发现20比30也要小，所以继续与30的左子树10进行比较。

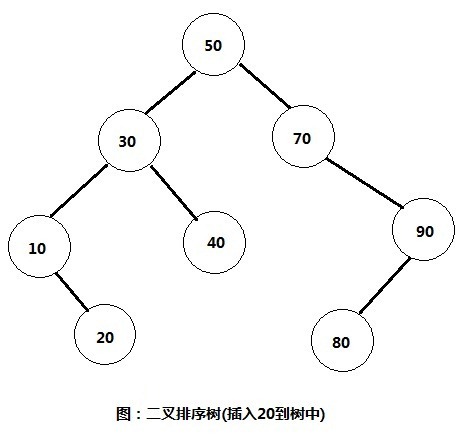
3) 发现20比10要大，所以就将20插入到10的右子树中。

此时二叉排序树效果如图：

2，查找节点

比如我们要查找节点10，那么思路如下：

1) 还是一样，首先将10与根节点50进行比较大小，发现比根节点要小，所以继续与根节点的左子树30进行比较。

2) 发现10比左子树30要小，所以继续与30的左子树10进行比较。

3) 发现两值相等，即查找成功，返回10的位置。

过程与插入相同，这里就不贴图了。

3，删除节点

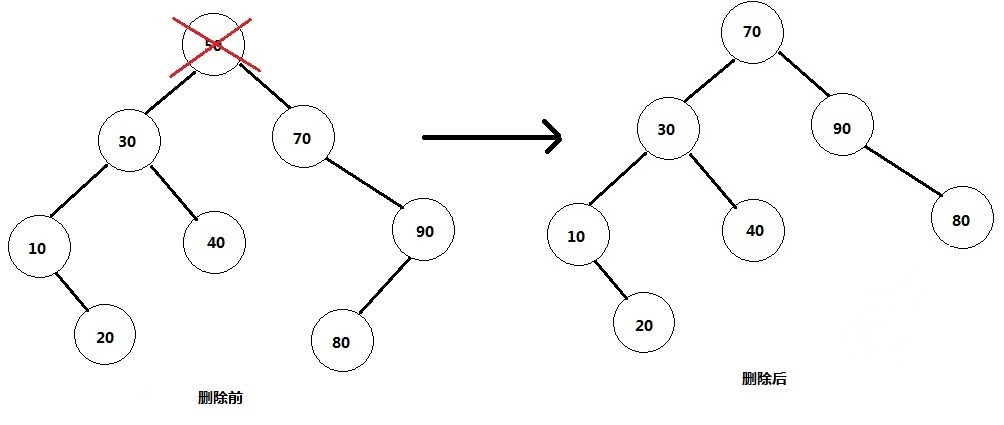
删除节点的情况相对复杂，主要分以下三种情形：

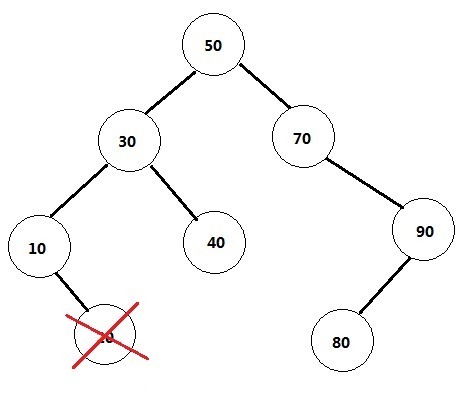
1) 删除的是叶节点(即没有孩子节点的)。比如20，删除它不会破坏原来树的结构，最简单。如图所示。

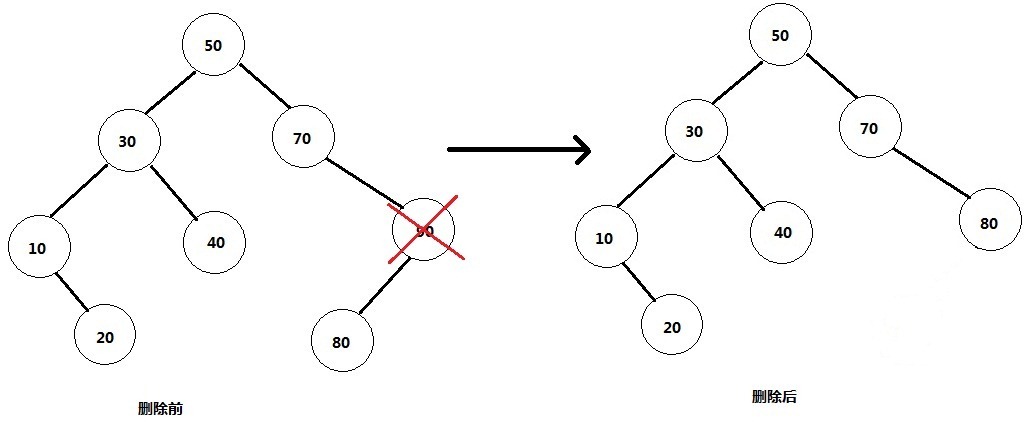
2) 删除的是单孩子节点。比如90，删除它后需要将它的孩子节点与自己的父节点相连。情形比第一种复杂一些。

3) 删除的是有左右孩子的节点。比如根节点50，这里有一个问题就是删除它后将谁做为根节点的问题？利用二叉树的中序遍历，就是右节点的左子树的最左孩子。

分析完了，有了思路之后，下面就开始写代码来实现这些功能了。

C#版：

namespace DS.BLL
{
    /// <summary>
    /// Description:二叉排序树的常见操作
    /// Author:McgradyLu
    /// Time:8/24/2013 4:12:18 PM
    /// </summary>
    public class BSTreeBLL
    {
        /// <summary>
        /// 创建二叉排序树
        /// </summary>
        /// <param name="list"></param>
        /// <returns></returns>
        public static BSTree Create(List<int> list)
        { 
            //创建根节点
            BSTree bsTree = new BSTree()
            { 
                Data=list[0],
                Left=null,
                Right=null
            };

            //将list中的节点一个一个地插入到二叉排序树中
            for (int i = 1; i < list.Count; i++) //注意这里从1开始，因为0位置上元素已经给了根节点
            {
                bool isExcute = false;
                Insert(bsTree, list[i], ref isExcute);
            }
            return bsTree;
        }

        /// <summary>
        /// 插入节点
        /// </summary>
        /// <param name="bsTree">二叉排序树</param>
        /// <param name="key">待插入值</param>
        /// <param name="isExcute">是否执行了if语句(节点是否插入)</param>
        public static void Insert(BSTree bsTree, int key, ref bool isExcute)
        {
            if (bsTree == null) return;

            //如果小于根节点，遍历左子树，否则遍历右子树(找到当前要插入节点的父节点)
            if (key < bsTree.Data) Insert(bsTree.Left, key, ref isExcute);
            else Insert(bsTree.Right, key, ref isExcute);

            if (!isExcute)
            {
                //创建当前节点
                BSTree current = new BSTree() { 
                    Data=key,
                    Left=null,
                    Right=null
                };

                //插入到父节点中
                if (key < bsTree.Data) bsTree.Left = current;
                else bsTree.Right = current;
                isExcute = true;
            }
        }

        /// <summary>
        /// 中序遍历
        /// </summary>
        /// <param name="bsTree"></param>
        public static void LDR(BSTree bsTree)
        {
            if (bsTree != null)
            {
                //遍历左子树
                LDR(bsTree.Left);

                //输出节点数据
                Console.Write(bsTree.Data+" ");

                //遍历右子树
                LDR(bsTree.Right);
            }
        }

        /// <summary>
        /// 查找节点
        /// </summary>
        /// <param name="bsTree">待查找的二叉排序树</param>
        /// <param name="key"></param>
        /// <returns>true表示查找成功，false表示查找失败</returns>
        public static bool Search(BSTree bsTree, int key)
        {
            //遍历完没有找到，查找失败
            if (bsTree == null) return false;

            //要查找的元素为当前节点,查找成功
            if (key == bsTree.Data) return true;

            //继续去当前节点的左子树中查找，否则去当前节点的右子树中查找
            if (key < bsTree.Data) return Search(bsTree.Left, key);
            else return Search(bsTree.Right,key);
        }

        /// <summary>
        /// 删除节点
        /// </summary>
        /// <param name="bsTree"></param>
        /// <param name="key"></param>
        public static void Delete(ref BSTree bsTree, int key)
        {
            //空树
            if (bsTree == null) return;

            //判断是否是要删除的节点
            if (key == bsTree.Data)
            { 
                //第一种情况：叶子节点(没有孩子节点)
                if (bsTree.Left == null && bsTree.Right == null)
                {
                    bsTree = null;
                    return;
                }

                //第二种情况：仅有左子树
                if (bsTree.Left != null && bsTree.Right == null)
                {
                    bsTree = bsTree.Left;
                    return;
                }

                //第三种情况：仅有右子树
                if (bsTree.Left == null && bsTree.Right != null)
                {
                    bsTree = bsTree.Right;
                    return;
                }

                //第四种情况：有左，右子树
                if (bsTree.Left != null && bsTree.Right != null)
                { 
                    //利用中序遍历找到右节点的左子树的最左孩子
                    var node = bsTree.Right;
                    while (node.Left != null)
                    {
                        node = node.Left;
                    }

                    node.Left = bsTree.Left;
                    if (node.Right == null)
                    {
                        Delete(ref bsTree,node.Data);
                        node.Right = bsTree.Right;
                    }
                    bsTree = node;
                }
            }

            //遍历找到要删除的节点
            if (key < bsTree.Data)
            {
                Delete(ref bsTree.Left, key);
            }
            else
            {
                Delete(ref bsTree.Right, key);
            }
        }
    }

    /// <summary>
    /// 封装二叉排序树结构
    /// </summary>
    public class BSTree
    {
        public int Data;

        public BSTree Left;

        public BSTree Right;
    }
}

namespace BSTSearch.CSharp
{
    class Program
    {
        static void Main(string[] args)
        {
            List<int> list = new List<int> { 50,30,70,10,40,90,80};

            Console.WriteLine("***************创建二叉排序树***************");
            BSTree bsTree = BSTreeBLL.Create(list);
            Console.Write("中序遍历的原始数据:\n");
            BSTreeBLL.LDR(bsTree);

            Console.WriteLine("\n********************查找节点********************");
            Console.WriteLine("元素40是否在树中:{0}",BSTreeBLL.Search(bsTree,40));

            Console.WriteLine("\n********************插入节点********************");
            Console.WriteLine("将元素20插入到树中");
            bool isExcute=false;
            BSTreeBLL.Insert(bsTree,20,ref isExcute);
            Console.Write("中序遍历后:\n");
            BSTreeBLL.LDR(bsTree);

            Console.WriteLine("\n********************删除节点1********************");
            Console.WriteLine("删除叶子节点20,\n中序遍历后:\n");
            BSTreeBLL.Delete(ref bsTree,20);
            BSTreeBLL.LDR(bsTree);

            Console.WriteLine("\n********************删除节点2********************");
            Console.WriteLine("删除单孩子节点90,\n中序遍历后:\n");
            BSTreeBLL.Delete(ref bsTree, 90);
            BSTreeBLL.LDR(bsTree);

            Console.WriteLine("\n********************删除节点2********************");
            Console.WriteLine("删除根节点50,\n中序遍历后:\n");
            BSTreeBLL.Delete(ref bsTree, 50);
            BSTreeBLL.LDR(bsTree);

            Console.ReadKey();
        }
    }
}

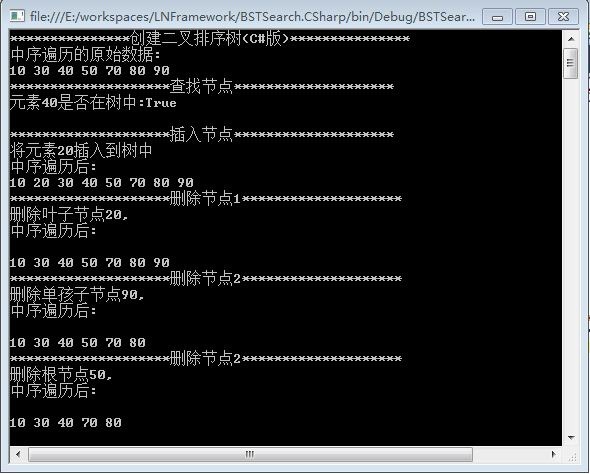
程序输出结果如图：

 

C语言版：

/*包含头文件*/
#include "stdio.h"
#include "stdlib.h"   
#include "io.h"
#include "math.h" 
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20

typedef int Status; 

/* 二叉树的二叉链表结点结构定义 */
typedef  struct BiTNode    /* 结点结构 */
{
    int data;    /* 结点数据 */
    struct BiTNode *lchild, *rchild;    /* 左右孩子指针 */
} BiTNode, *BiTree; /**BiTree等价于typedef BiTNode *BiTree*/

/*查找二叉排序树T中是否存在key(递归查找)*/
Status Search(BiTree T, int key, BiTree f, BiTree *p)
{
    if (!T)    /*  查找不成功 */
    { 
        *p = f;  
        return FALSE; 
    }
    else if (key==T->data) /*  查找成功 */
    { 
        *p = T;  
        return TRUE; 
    } 
    else if (key<T->data) 
        return Search(T->lchild, key, T, p);  /*  在左子树中继续查找 */
    else  
        return Search(T->rchild, key, T, p);  /*  在右子树中继续查找 */
}

/*  当二叉排序树T中不存在关键字等于key的数据元素时， */
/*  插入key并返回TRUE，否则返回FALSE */
Status Insert(BiTree *T, int key)
{
    BiTree p,s;
    if (!Search(*T, key, NULL, &p)) /* 查找不成功 */
    {
        s = (BiTree)malloc(sizeof(BiTNode));
        s->data = key;  
        s->lchild = s->rchild = NULL;  
        if (!p) 
            *T = s;            /*  插入s为新的根结点 */
        else if (key<p->data) 
            p->lchild = s;    /*  插入s为左孩子 */
        else 
            p->rchild = s;  /*  插入s为右孩子 */
        return TRUE;
    } 
    else 
        return FALSE;  /*  树中已有关键字相同的结点，不再插入 */
}

/* 从二叉排序树中删除结点p，并重接它的左或右子树。 */
Status DeleteBST(BiTree *p)
{
    BiTree q,s;
    if((*p)->rchild==NULL) /* 右子树空则只需重接它的左子树（待删结点是叶子也走此分支) */
    {
        q=*p; *p=(*p)->lchild; free(q);
    }
    else if((*p)->lchild==NULL) /* 只需重接它的右子树 */
    {
        q=*p; *p=(*p)->rchild; free(q);
    }
    else /* 左右子树均不空 */
    {
        q=*p; s=(*p)->lchild;
        while(s->rchild) /* 转左，然后向右到尽头（找待删结点的前驱） */
        {
            q=s;
            s=s->rchild;
        }
        (*p)->data=s->data; /*  s指向被删结点的直接前驱（将被删结点前驱的值取代被删结点的值） */
        if(q!=*p)
            q->rchild=s->lchild; /*  重接q的右子树 */ 
        else
            q->lchild=s->lchild; /*  重接q的左子树 */
        free(s);
    }
    return TRUE;
}

/* 若二叉排序树T中存在关键字等于key的数据元素时，则删除该数据元素结点, */
/* 并返回TRUE；否则返回FALSE。 */
Status Delete(BiTree *T,int key)
{ 
    if(!*T) /* 不存在关键字等于key的数据元素 */ 
        return FALSE;
    else
    {
        if (key==(*T)->data) /* 找到关键字等于key的数据元素 */ 
            return DeleteBST(T);
        else if (key<(*T)->data)
            return Delete(&(*T)->lchild,key);
        else
            return Delete(&(*T)->rchild,key);

    }
}

/*二叉树中序遍历*/
void LDR(BiTree T)
{
    if (T!=NULL)
    {
        LDR(T->lchild);
        printf("%d ",T->data);
        LDR(T->rchild);
    }
}


#define N 10
void main()
{
    int i,j;
    BiTree T=NULL;

    //定义数组和初始化SeqList
    int d[N]={62,88,58,47,35,73,51,99,37,93};

    for (i=0;i<N;i++)
    {
        Insert(&T,d[i]);
    }

    printf("***************二叉排序树查找(C版)***************\n");
    printf("初始化二叉排序树\n中序遍历数据：");
    LDR(T);

    printf("\n***************删除节点1***************\n");
    Delete(&T,93);
    printf("删除叶节点93\n中序遍历后：");
    LDR(T);

    printf("\n***************删除节点2***************\n");
    Delete(&T,47);
    printf("删除双孩子节点47\n中序遍历后：");
    LDR(T);

    getchar();
}

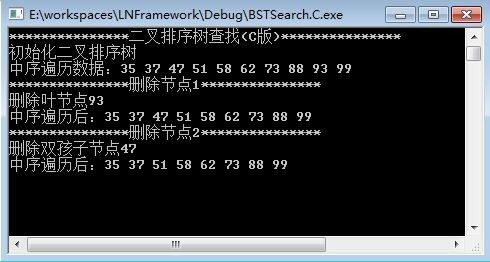
程序输出结果如图：