普通生成函数(OGF)
形式
F=∑n≥0 fn xn
基本运算
1.相加
F±G=∑n≥0 (fn±gn) xn
2.卷积
F⋅G=∑n≥0 xn n∑i=0fign−i
几种常见的幂级数求和
f=0,1,1,1,...数列f的生成函数:F=∑n≥0xn=x1−x
f=1,0,1,0,1,0,...数列f的生成函数:F=∑n≥0x2n=11−x2
f=1,2,3,4,...数列f的生成函数:F=∑n≥0(n+1)xn=1(1−x)2
fn=Cnm数列f的生成函数:F=∑n≥0Cnmxn=(1+x)m
fn=Cnn+m数列f的生成函数:F=∑n≥0Cnn+mxn=1(1−x)m+1
- 多项式定理
(x1+x2+...+xn)k=∑α1+α2+...+αnk!α1!α2!...αn!xα11...xαnn

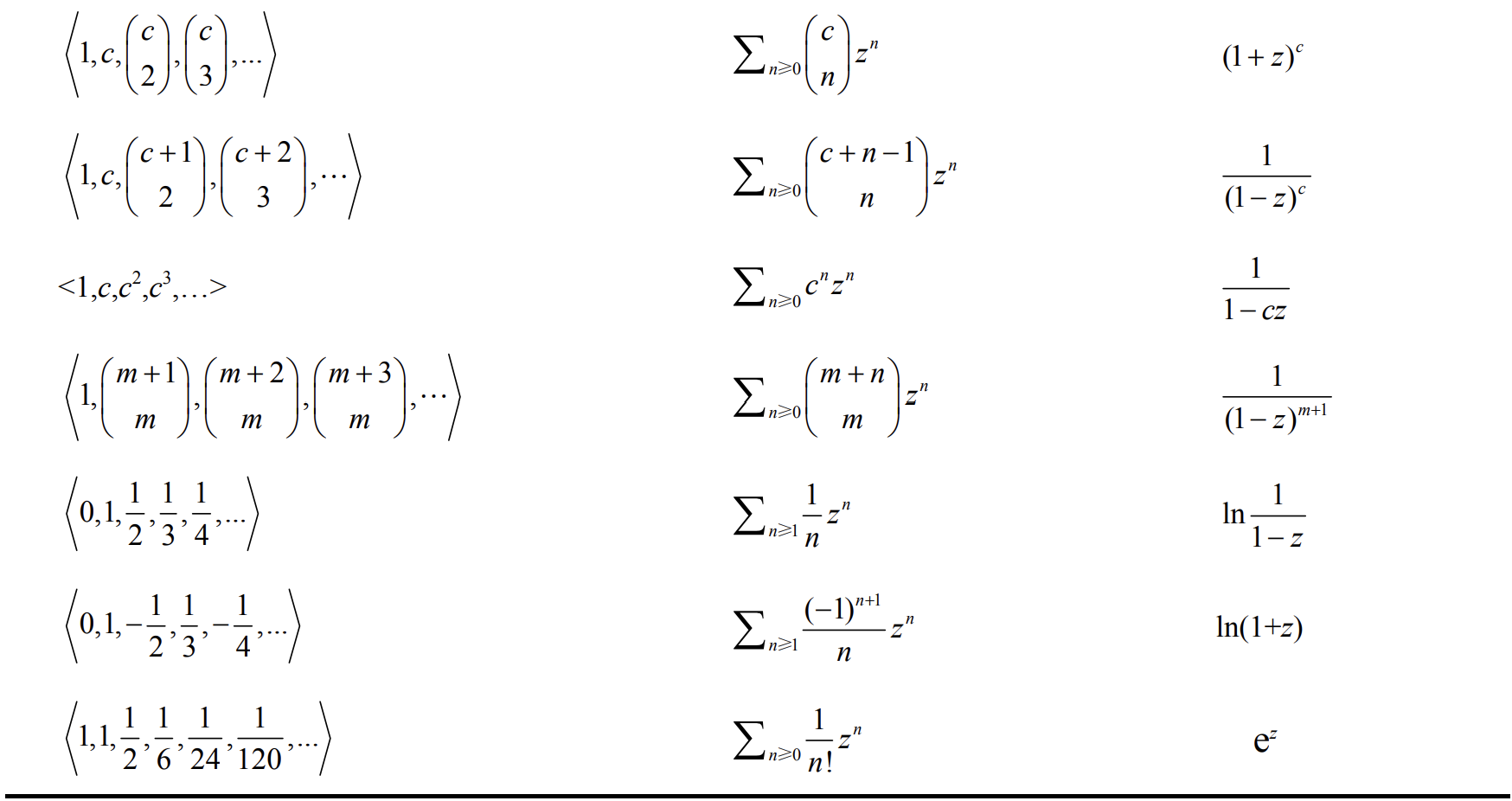
指数生成函数(EGF)
形式:
F=∑n≥0fnxnn!
卷积:
F⋅G=∑n≥0fnxnn!⋅∑n≥0gnxnn!=∑n≥0xnn!n∑i=0Cinfign−i
二项式反演
形式:
若
gn=n∑i=0Cinfi
则
fn=n∑i=0(−1)n−i Cin gi
其中fn可以理解为恰好n个不同的元素形成特定结构的方案数,gn可以理解为至多n个不同的元素形成特定结构的方案数
证明:
fn=n∑i=0Cin(−1)n−i (i∑j=0Cjifj)=n∑i=0i∑j=0CinCji(−1)n−ifj=n∑j=0n∑i=jCinCji(−1)n−ifj=n∑j=0fjn∑i=jCinCji(−1)n−i
因为:Crn Ckr=Ckn Cr−kn−k
所以:
fn=n∑j=0fjn∑i=jCjnCi−jn−j(−1)n−i=n∑j=0Cjnfjn∑i=jCi−jn−j(−1)n−i=令k=i−j n∑j=0Cjnfjn−j∑k=0Ckn−j(−1)n−j−k=n∑j=0Cjnfj[n−j=0]=n∑j=0Cjnfj[n=j]=fn
另一种形式:
若
gk=n∑i=kCkifi
则
fk=n∑i=k(−1)i−k Cki gi
其中fn可以理解为恰好n个不同的元素形成特定结构的方案数,gn可以理解为至少n个不同的元素形成特定结构的方案数
第二个形式比价容易用容斥原理来理解,然后可以通过类比来想第一种形式。
例:P4491 [HAOI2018] 染色
题解

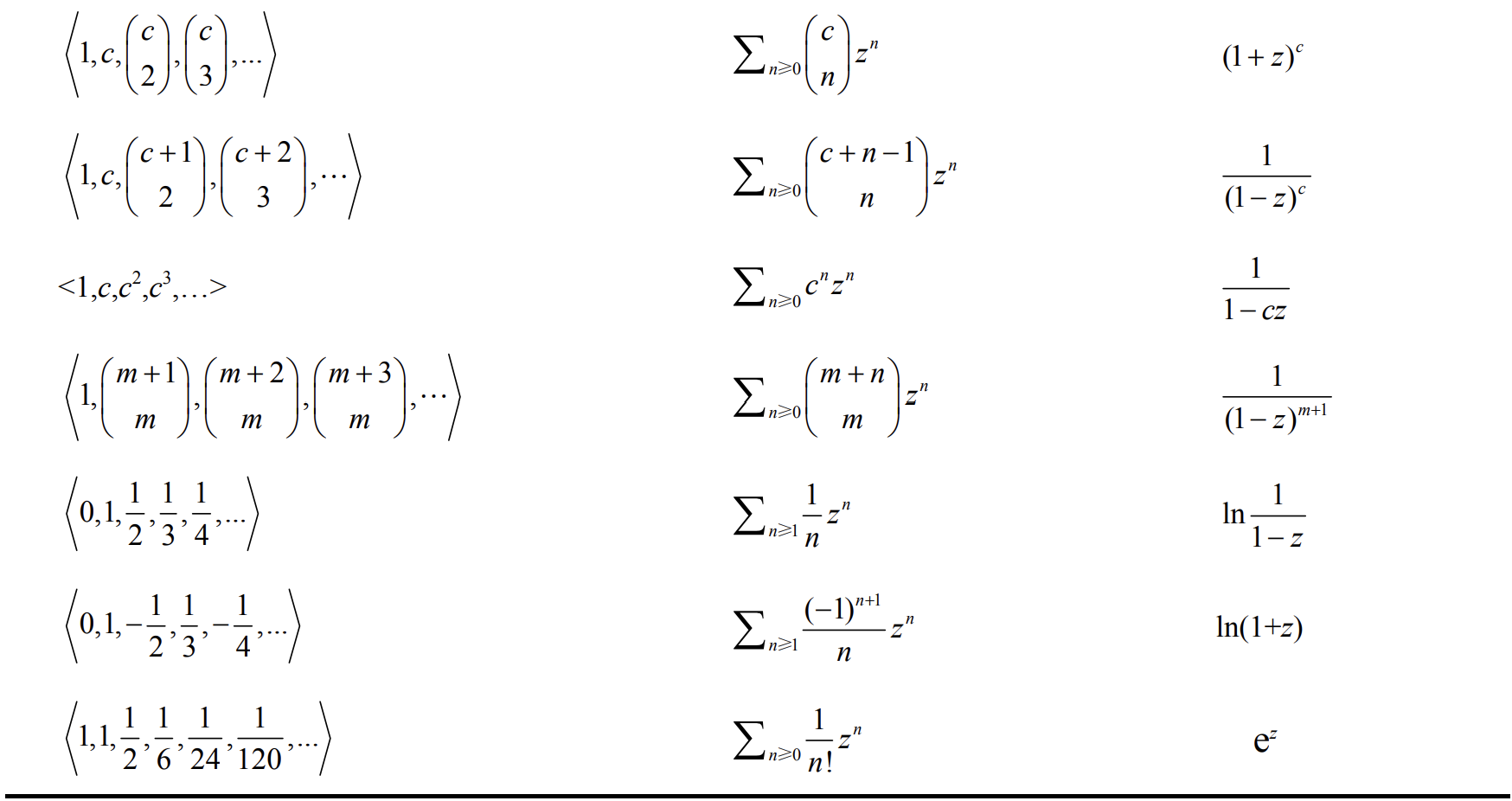


.PNG)

【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识?