CS61B-union-find（并查集）算法

一、备注：union-find又名Disjoint-Sets，所以union-find是不允许有重复数据的。

 

二、应用：解决动态连通性问题

 

三、分析：当不断有新节点加入时，需要完成的操作：（1）判断2个节点是否在同一个集合中isConnected(p, q)；（2）将某一个节点所在集合中的节点都合并到另一个节点所在的集合中 connect(p, q)

 

 

四、思路：（1）定义一种数据结构（数组）表示已知的连接

（2）基于此数据结构实现高效的操作

 

五、实现：

先能完成功能，再分析效率进行迭代优化

1.quick-find算法实现

 

 

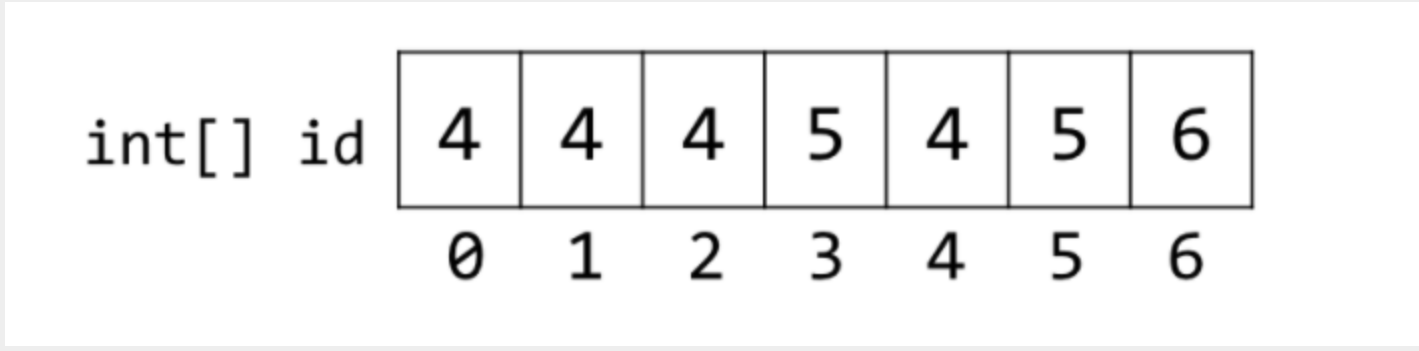
 使用数组，索引表示数据，值表示集合的标号，如：0, 1, 2, 4都在一个集合（4）中；3, 5在同一个集合（5）中，6在一个集合（6）中。

对于isConnected(p, q)：可以使用 id[p] == id[q]进行判断

对于connect(p, q)：可以遍历一次数组，将值等于id[p]的改成id[q]（或者反过来，id[q]的值改成id[p]也行）

//定义一个接口，后面的算法也会用到
public interface UnionFind {
    boolean isConnected(int p, int q);

    void connect(int p, int q);
}

//quick-find代码实现
public class QuickFind implements UnionFind {
    private int[] id;
    public QuickFind(int N) {
        id = new int[N];
        for (int i = 0; i < id.length; i++) {
            id[i] = i;          //表示初始化的状态
        }
    }
    @Override
    public boolean isConnected(int p, int q) {
        return (id[p] == id[q]);
    }

    @Override
    public void connect(int p, int q) {
        int pid = id[p];
        int qid = id[q];
        if (pid == qid) {
            return;
        }
        for (int i = 0; i < id.length; i++) {
            if (id[i] == pid) {
                id[i] = qid;
            }
        }
    }
}

时间复杂度分析：查找操作（isConnected）是O(1)，合并操作是O(n)，因此叫做quick-find。但对于实际中大规模的问题，每增加一对输入，就要遍历一次数组，效率太低。

 

2、quick-union算法实现

实现前的说明：

1. 此处需要引入树的结构进行可视化展示；另外，若要完成以上2个操作，需要先找到每棵树的根节点。因为假设输入是（p,q）：

（1）若p和q的根节点相同则属于同一个集合，返回true；

（2）若要将p和q所在的集合进行合并时，将某一棵树的根节点挂到另一棵树的根节点上。

所以需要加一个寻找根节点 find(int p）的操作。

一个具体的实例如下：

 

 

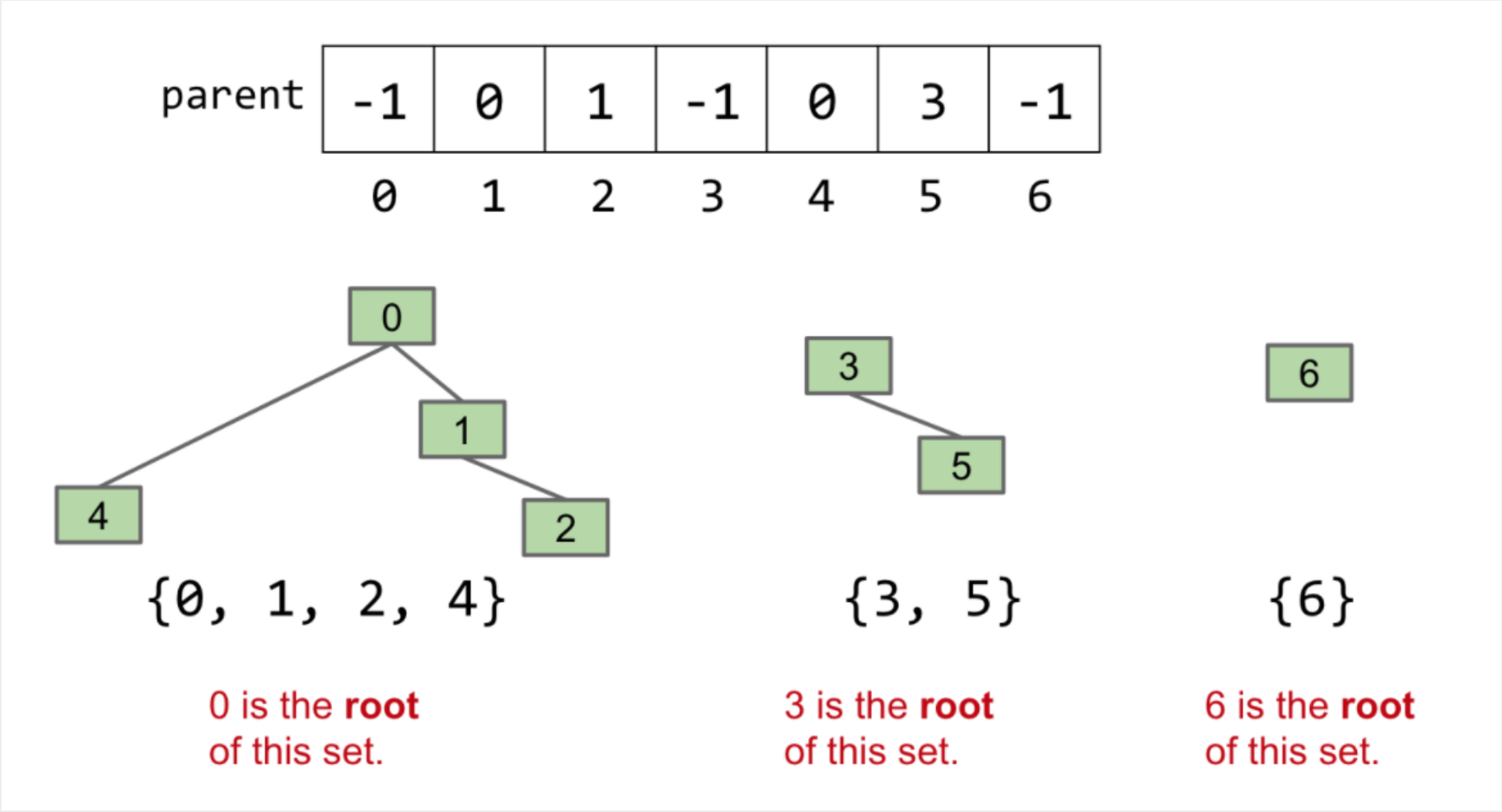
 以{0, 1, 2, 4}为例：数组的索引即代表存储的每一个数据，4的父节点是0，因此索引4的值0；2的父节点是1，因此索引2的值1；0是根节点没有父节点，因此以一个负数表示（这里取-1）

//quick-union代码实现
public class QuickUnion implements UnionFind {
    private int[] parent;
    public QuickUnion(int N) {
        parent = new int[N];
        for (int i = 0; i < N; i++) {
            parent[i] = i;
        }
    }

    //寻找根节点
    private int find(int p) {
        while (parent[p] >= 0) {
            p = parent[p];
        }
        return p;
    }

    @Override
    public boolean isConnected(int p, int q) {
        return (find(p) == find(q));
    }

    @Override
    public void connect(int p, int q) {
        if (find(p) == find(q)) {
            return;
        }
        int pid = find(p);
        int qid = find(q);
        parent[pid] = qid;
    }
}

　　时间复杂度分析：由于quick-union的查、并都用了find方法，因此在最坏的情况下（退化成一条链）都是O(n)；但相比于quick-find在合并上很多情况要好。当然，这只是中间一个过渡方案。

 

3、Weighted Quick Union（加权Quick Union）

quick-union为了让时间复杂度尽可能小，合并后的树的高度应当尽可能小。定义树的大小是指树的所有节点数。因此合并时，应当将小树连接到大树上。至于树的大小，可以选择另外建一个数组来保存，也可以将根节点的值设为大小的负数，即取代上面Quick Union的-1的位置。

//Weighted Quick Union代码实现
public class WeightedQuickUnion implements UnionFind {
    private int[] parent;
    private int[] size;
    public WeightedQuickUnion(int N) {
        parent = new int[N];
        size = new int[N];
        for (int i = 0; i < parent.length; i++) {
            parent[i] = i;          //表示初始化的状态
        }
        for (int i = 0; i < parent.length; i++) {
            size[i] = 1;
        }
    }

    private int find(int p) {
        while (parent[p] >= 0) {
            p = parent[p];
        }
        return p;
    }

    @Override
    public boolean isConnected(int p, int q) {
        return (find(p) == find(q));
    }

    @Override
    public void connect(int p, int q) {
        if (find(p) == find(q)) {
            return;
        }
        if (size[p] > size[q]) {
            parent[find(q)]= find(p);
            size[p] += size[q];
        } else {
            parent[find(p)]= find(q);
            size[q] += size[p];
        }
    }
}

　　时间复杂度分析：由于加权quick-union的构造原因，导致任一节点的最大深度等于整棵树的高度——logN。所以find在最坏情况下，即叶子节点去找跟节点的时间复杂度是logN，又由于查找和合并都是用的find方法，所以时间复杂度都是logN

 

4、Weighted Quick Union with Path Compression（路径压缩的加权quick-union）

在查找根节点时，将过程中遍历到的节点的父节点都改成根节点，即connect(5, 7)

 

 

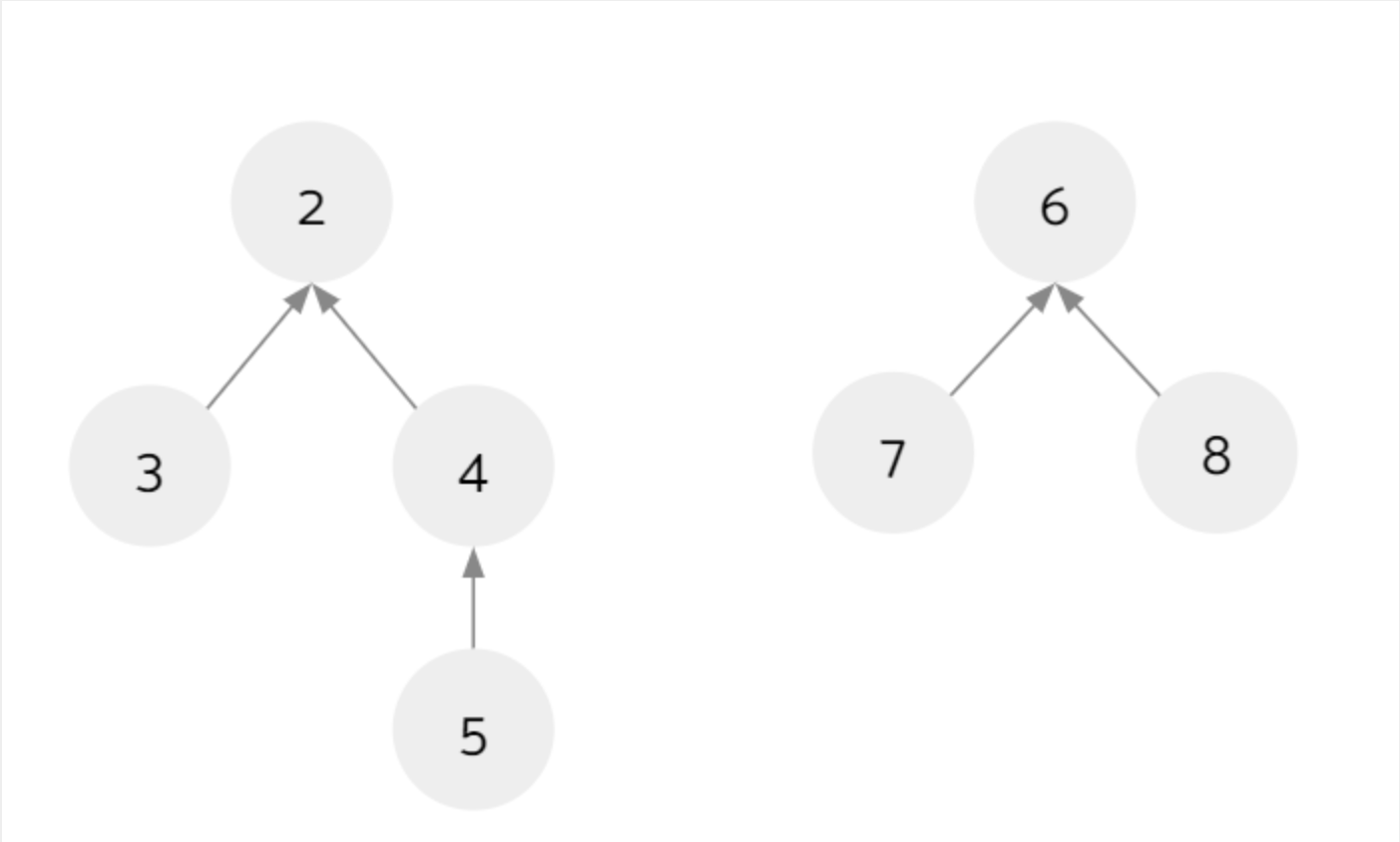
 最终变成

 

 

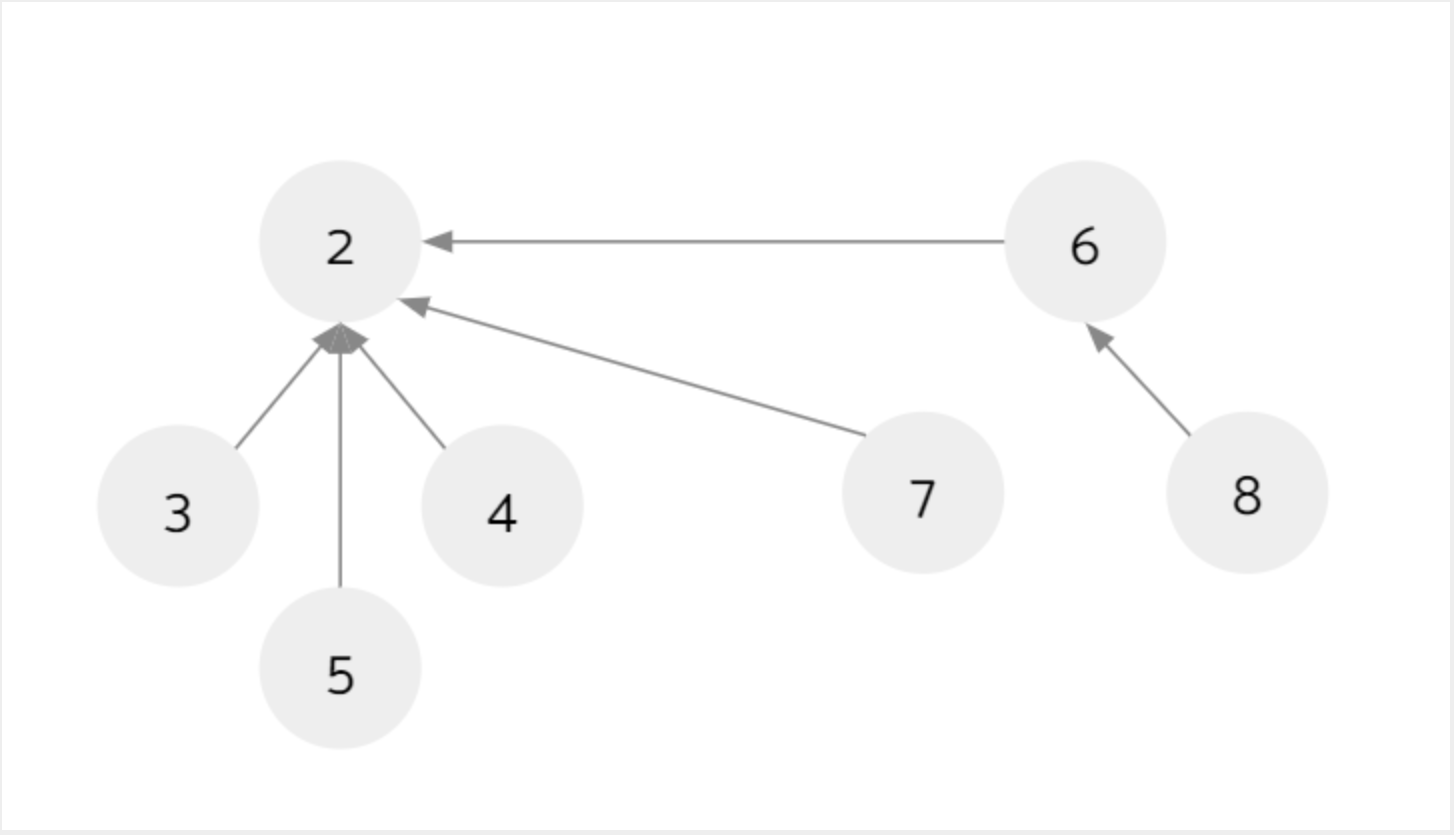
//Weighted Quick Union with Path Compression的代码在find方法中加一个循环即可
private int find(int p) {
    while (parent[p] >= 0) {
        p = parent[p];
    }
    int origin = p;
    while (origin != p) {
        int tmp = origin;
        origin = parent[origin];
        parent[tmp] = p;
     }
    return p;
}

　　复杂度分析：按资料中介绍说，十分接近O(1)，已是最优解。

备注：union-find又名Disjoint-Sets，所以union-find是不允许有重复数据的。

应用：解决动态连通性问题

分析：当不断有新节点加入时，需要完成的操作：（1）判断2个节点是否在同一个集合中 isConnected(p, q)；（2）将某一个节点所在集合中的节点都合并到另一个节点所在的集合中 connect(p, q)

思路：（1）定义一种数据结构（数组）表示已知的连接

（2）基于此数据结构实现高效的操作

实现：

先能完成功能，再分析效率进行迭代优化

1.quick-find算法实现

​使用数组，索引表示数据，值表示集合的标号，如：0, 1, 2, 4都在一个集合（4）中；3, 5在同一个集合（5）中，6在一个集合（6）中。

对于：可以使用 id[p] == id[q]进行判断

对于connect(p, q)：可以遍历一次数组，将值等于id[p]的改成id[q]（或者反过来，id[q]的值改成id[p]也行）

//定义一个接口，后面的算法也会用到
  public interface UnionFind {
      boolean isConnected(int p, int q);
  ​
      void connect(int p, int q);
  }
  //quick-find代码实现
  public class QuickFind implements UnionFind {
      private int[] id;
      public QuickFind(int N) {
          id = new int[N];
          for (int i = 0; i < id.length; i++) {
              id[i] = i;          //表示初始化的状态
          }
      }
      @Override
      public boolean isConnected(int p, int q) {
          return (id[p] == id[q]);
      }
  ​
      @Override
      public void connect(int p, int q) {
          int pid = id[p];
          int qid = id[q];
          if (pid == qid) {
              return;
          }
          for (int i = 0; i < id.length; i++) {
              if (id[i] == pid) {
                  id[i] = qid;
              }
          }
      }
  }

 

  ​

时间复杂度分析：查找操作（isConnected）是O(1)，合并操作是O(n)，因此叫做quick-find。但对于实际中大规模的问题，每增加一对输入，就要遍历一次数组，效率太低。

 

2、quick-union算法实现

实现前的说明：

1. 此处需要引入树的结构进行可视化展示；另外，若要完成以上2个操作，需要先找到每棵树的根节点。因为假设输入是（p,q）：

（1）若p和q的根节点相同则属于同一个集合，返回true；

（2）若要将p和q所在的集合进行合并时，将某一棵树的根节点挂到另一棵树的根节点上。

所以需要加一个寻找根节点 find(int p）的操作。

一个具体的实例如下：

以{0, 1, 2, 4}为例：数组的索引即代表存储的每一个数据，4的父节点是0，因此索引4的值0；2的父节点是1，因此索引2的值1；0是根节点没有父节点，因此以一个负数表示（这里取-1）

//quick-union代码实现
  public class QuickUnion implements UnionFind {
      private int[] parent;
      public QuickUnion(int N) {
          parent = new int[N];
          for (int i = 0; i < N; i++) {
              parent[i] = i;
          }
      }
  ​
      //寻找根节点
      private int find(int p) {
          while (parent[p] >= 0) {
              p = parent[p];
          }
          return p;
      }
  ​
      @Override
      public boolean isConnected(int p, int q) {
          return (find(p) == find(q));
      }
  ​
      @Override
      public void connect(int p, int q) {
          if (find(p) == find(q)) {
              return;
          }
          int pid = find(p);
          int qid = find(q);
          parent[pid] = qid;
      }
  }
  ​

 

时间复杂度分析：由于quick-union的查、并都用了find方法，因此在最坏的情况下（退化成一条链）都是O(n)；但相比于quick-find在合并上很多情况要好。当然，这只是中间一个过渡方案。

 

3、Weighted Quick Union（加权Quick Union）

quick-union为了让时间复杂度尽可能小，合并后的树的高度应当尽可能小。定义树的大小是指树的所有节点数。因此合并时，应当将小树连接到大树上。

//Weighted Quick Union代码实现
  public class WeightedQuickUnion implements UnionFind {
      private int[] parent;
      private int[] size;
      public WeightedQuickUnion(int N) {
          parent = new int[N];
          size = new int[N];
          for (int i = 0; i < parent.length; i++) {
              parent[i] = i;          //表示初始化的状态
          }
          for (int i = 0; i < parent.length; i++) {
              size[i] = 1;
          }
      }
  ​
      private int find(int p) {
          while (parent[p] >= 0) {
              p = parent[p];
          }
          return p;
      }
  ​
      @Override
      public boolean isConnected(int p, int q) {
          return (find(p) == find(q));
      }
  ​
      @Override
      public void connect(int p, int q) {
          if (find(p) == find(q)) {
              return;
          }
          if (size[p] > size[q]) {
              parent[find(q)]= find(p);
              size[p] += size[q];
          } else {
              parent[find(p)]= find(q);
              size[q] += size[p];
          }
      }
  }

时间复杂度分析：由于加权quick-union的构造原因，导致任一节点的最大深度等于整棵树的高度——logN。所以find在最坏情况下，即叶子节点去找跟节点的时间复杂度是logN，又由于查找和合并都是用的find方法，所以时间复杂度都是logN

 

4、Weighted Quick Union with Path Compression（路径压缩的加权quick-union）

在查找根节点时，将过程中遍历到的节点的父节点都改成根节点，即connect(5, 7)

最终变成

//Weighted Quick Union with Path Compression的代码在find方法中加一个循环即可
  private int find(int p) {
  while (parent[p] >= 0) {
  　　p = parent[p];
  }
      int origin = p;
      while (origin != p) {
          int tmp = origin;
          origin = parent[origin];
          parent[tmp] = p;
       }
  return p;
  }

 

　　总结：

quick-find：重点是find，通过将同一个set的节点设为相等值，能实现O(1)的查找效率

quick-union：重点是union，通过设置父节点，使得合并时查找根节点的时间复杂度能在某些情况下小于O(n)

weighted-quick-union：重点是在quick-union基础上引入size（树的大小），将小树合并到大树下，降低一些树的高度，使得时间复杂度达到O(logn)

weighted-quick-union-with path compression：重点是路径压缩（每次调用find方法时进一步地降低树的高度），使得时间复杂度接近于O(1)

 

练习：判断下图中A~F哪个可能是路径压缩的带权quick-union

 

 

 

 

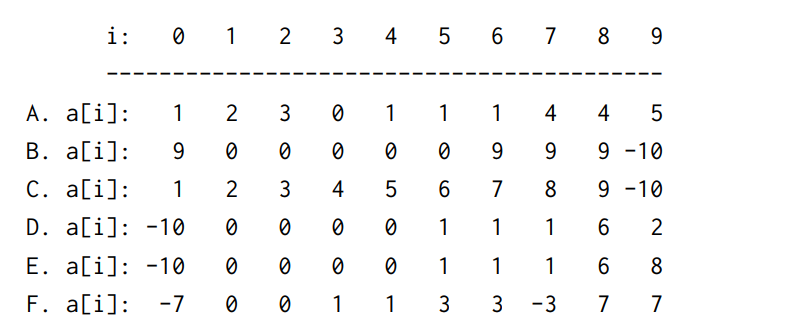
答：只有D可能是，首先带环肯定不是；其次不能有大树连到小树上情况；最后树的高度不能大于lgN

参考资料：Berkeley-CS61B课程 & 《算法第四版》