切线空间（Tangent Space）法线映射（Normal Mapping）【转】

请注明出处：http://blog.csdn.net/BonChoix，谢谢~）

切线空间（Tangent Space）

切换空间，同局部空间、世界空间等一样，是3D图形学中众多的坐标系之一。切换空间最重要的用途之一，即法线映射（Normal Mapping）。关于法线映射的细节，将在下一篇文章中详细介绍。但在学习法线映射之前，深刻地理解切换空间非常重要。因此借这一篇文章来学习下它，以为后面学习法线映射、视差映射（Parallax Mapping）、Displacement Mapping等技术作准备。Parallax mapping、Displacement Mapping都属于bump mapping范畴，而且都基于Normal Mapping, 但相比Normal Mapping，后两种方法可以提供更加逼真物体表面的凹凸感。

1. 为什么要有切线空间？

在3D世界中定了如此多的坐标系，每个坐标系当然都有它的用途。比如局部空间，或者叫模型空间，它的目的就是方便我们对3D模型进行建模。在这个空间中，我们不需要考虑该模型在场景中可能出现的位置、朝向等众多细节，而专注于模型本身。在世界空间中，我们关心的问题是场景中各个物体的位置、朝向，即如何构建场景，而不必关注摄像机的观察位置及其朝向。可见，一个坐标系的根本用途，即让我们在处理不同的问题时，能够以合适的参照系，抛开不相关的因素，从而减小问题的复杂度。

直观地讲，模型顶点中的纹理坐标，就定义于切线空间。普通2维纹理坐标包含U、V两项，其中U坐标增长的方向，即切线空间中的tangent轴，V坐标增加的方向，为切线空间中的bitangent轴。模型中不同的三角形，都有对应的切线空间，其tangent轴和bitangent轴分别位于三角形所在平面上，结合三角形面对应的法线，我们称tangant轴（T）、bitangent轴（B）及法线轴（N）所组成的坐标系，即切线空间（TBN）。

如下图所示：

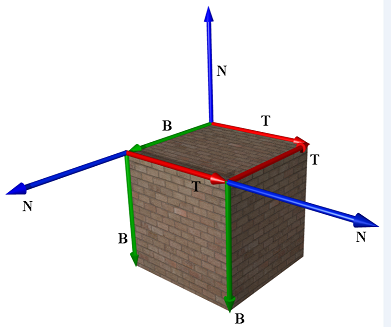
在立方体中，每个面都有对应的切线空间，每个面由两个三角形组成，该两个三角形中的纹理坐标就基于相应的切线空间。

2. 纹理坐标与位置坐标的关系

纹理坐标与位置坐标，可以通过切线空间联系起来。如下图所示：

该图显示了一个三角形及其所在的切线空间。已知该三角形三个顶点的位置坐标：V₀, V₁,V₂, 以及对应的纹理坐标：(u0,v0,), (u1, v1), (u2, v2)。定义三角形的两条边为E0 = V₁ –V₀，E1= V₂ – V₀，对应的纹理坐标差值：(t1, b1) = (u₁ – u₀, v₁– v₀)， (t2, b2) = (u₂ – u₀, v₂– v₀)。我们有如下关系式：

E₀ =t1T+ b1B

E₁ = t2T+ b2B

3. 切线坐标系的求法

有了以上纹理坐标与位置坐标的关系，我们便可以根据已知的信息，自己来求得任一三角形的切线坐标系了。在3D模型文件中，所有顶点的位置坐标、纹理坐标、法线等信息一般都会提供的，但却缺少切线坐标系相关信息。而在应用Normal Mapping等技术时，切线空间又是必不可少的，因此就需要我们自己手动来获取切线坐标系了。很多读取模型的库都提供了生成切线空间的功能，不过了解一下其是如何生成还是很有必要的。下面我们就来一步步地推导下切线空间的求法：

继续从上面的纹理坐标与位置坐标的关系公式出发，把它表示成矩阵形式为：

把E0,E1,T，B拆成分量形式，即：

把移到另一边，有：

根据矩阵知识，对于矩阵，其逆矩阵为：

因此以上公式可以进一步表示为：

至此，等号右边的数据都是已知的，因此左边的矩阵即可求得，从而得到切线空间中的T、B两轴。N轴即三角形面的法线，很容易求得。

4. 注意

现在我们根据三角形的顶点位置坐标与纹理坐标，求得了该三角形所在的切线空间。但有一点要注意，这里求得的T向量和B向量一般不是标准化的（长度不为1）。这与一般其他的坐标系有所区别。在局部空间、世界空间、视角空间中，其对应的X、Y、Z轴长度都为1，究其原因主要是这几个空间中的坐标所使用的度量单位都是一样的。而在切线空间中，针对的是纹理，而纹理坐标与位置坐标显然使用不同的度量单位，比如对于纹理坐标从0到1的变化，其对应的位置坐标变化是不确定的。

因此，这里求得T和B向量长度一般不为1，而且对于有纹理坐标变换的情形，T和B两轴甚至不会相互垂直。

但是，在大多数情况下，我们只需要标准化后和T、B、N向量，而不关心其相应的长度。比如在Normal Mapping中，我们使用TBN坐标系的目的只是为了把从Normal Map中得到的法线从切线空间转换到世界空间，与纹理坐标无任何关联，因此这里我们使用的TNB坐标系的三个轴全是准备化的。

5. 顶点的切线空间

上面的方法求到的切线空间是基于单个三角形的，而在3D管线中，我们的处理是基于顶点进行的。因此我们需要获得顶点对应的切线空间。不过有了每个三角形的切换空间，每个顶点的切线空间就很容易处理了，即对于任一顶点，我们使用其所在的所有三角形所对应的切线空间向量的平均值，作为该顶点的切线空间。熟悉法线求法的可能会发现，这种方法与通过三角形法线求取顶点法线的方法思路是完全一样的。

切线空间的加入，使得我们的顶点定义也要发现相应的更改了。切线空间包括TBN三个向量，大多数情况下，我们使用的切线空间这三个向量都是准备化且相互垂直的，因此，对于每个顶点，我们只要提供T、N两个向量即可，在运行时通过向量叉乘临时地计算B向量即可，这样也节省了每个顶点的数据量。

现在，我们的顶点的定义如下所示：

[cpp]

struct };

这正是我们在GeometryGens.h文件中生成常见几何体时统一使用的顶点格式。在之前的程序中，我们从未使用过tangent成员，其实它就是为后面学习Normal Mapping而准备滴~

法线映射

1. 为什么使用法线映射？

在开始正式讨论法线映射之前，先来看下以下两张图片：

这两张依然是之前一篇文章中用到的仙剑五前传中两张截图，两图中显示的为同一地点，不同的观察角度。在左边的图中，根据纹理图，它给人一种很粗糙的岩石壁的感觉，但右边图中却出现了强烈的高光反射。这显然是有点相互矛盾的，因为强烈的全反射只有在表面比较光滑的表面上才会出现，而从左图中来看，它应该是凹凸不平的。造成这种现象的原因很简单：纹理的使用给我们带来了像素级别上的物体表面的细节，而模型本身是由有限个顶点组成的，这样在像素着色器中，经过插值计算得到的各像素的法线是平滑过渡的，而不再是各像素本身应该有的法线值。这样平滑过渡的法线在经过光照计算后，就很容易造成这种比较明显的高光反射现象。

要修正这种现象，根本问题在于修改像素的法线值，使其与真实法线趋于一致，这样在光照计算后将会得到与实际逼近的结果。要实现这种效果，有两种方法：一种是增加模型的细节，即顶点个数，这样就可以为模型表面指定更多的法线，而不再是在像素着色阶段依赖简单的插值计算得到，以得到更加真实的效果。这种方法是可行的，但有一个缺陷，更多的顶点意味着更大的计算量，因为在顶点着色器中，每个顶点都要经过各自的各种矩阵变换。因此这种方法能够提供的细节程度是有限的，一般不足以满足我们的要求。另一种效率非常高而且效果很好的方法，即这篇文章的主题：Normal Mapping。

2. 法线贴图及其数据格式

在Normal Mapping技术中，需要使到到一张纹理。与普通纹理不同的是，这张纹理中的每个像素（texel）存放的并不是颜色值，而是法线，因此也称之为法线贴图（Normal Map）。我们知道，纹理的使用给基于顶点的几何模型带来了像素级别上的细节，同样，法线贴图的使用，使用我们能够得到模型表面在像素级别上的法线值，这样的法线值是直接通知读取纹理获得的，而不再是经过插值得到，因此可以根据现实需求由美工们灵活设定，以获得想要的逼真效果。

在数据存放格式上，法线贴图与普通贴图并无差别，依然是RGB格式或者RGBA格式。只是这里的R、G、B、A不再是颜色的不同分量，而是三维法线向量的各分量。R、G、B分别代表法向量的X、Y、Z分量，如果是RGBA格式，则一般可以用A分量来存放高度信息。这个高度信息也是非常有用的，在很多地方需要与法线值配对使用，比如Parallax Mapping（后面介绍）。这里我们主要来关注RGB分量。一般情况下各分量占8个位（无符号），因此取值区间位于[0, 255]。但在实际情况下，经过归一化的法线向量，总长度为1，因此各分量都位于[-1, 1]之间。因此要想使用8位来存放，需要把[-1, 1]范围映射到[0, 255]之间。方法其实很简单，令x为[-1, 1]中任意值，通过y = (x + 1) /2 * 255，即得到了位于[0, 255]之间的y。相反，对于从贴图中读取到的y值，我们可以通过反向变换：x = 2*y / 255 - 1，得到我们想要的范围区间内的值。

在HLSL中，通过内置函数 Sample（与之前读取纹理的函数一样），我们可以直接得到位于[0, 1]之间的数据，因此我们只需要进行2*x - 1的变换即可。如下所示：

[cpp]

normal = g_normalMap.Sample(samplerTex, pin.tex).rgb;

normal = 2 * normal - 1;

3. 切线空间到世界空间

通过Sample函数，我们得到了任意像素上对应的法线值，下一步就可以利用这个法线来进行光照计算了。但实际上，这时得到的法线是不能直接用于光照计算的，而需要先进行相应的空间变换。这就是上一节中提到的“切线空间”的用途了。在上面提到的法线贴图中，里面所存放的法线值正是位于切线空间内，而场景中所提供的光源位于世界空间。要想进行正确的光照计算，需要把光源和法线转换到同一个空间中进行，要么统一位于切线空间，要么统一位于世界空间。（这里我们统一在世界空间进行光照计算）

关于在切线空间定义法线的目的，在这里我再进行一下补充。如果对切线空间还不是很理解，按我的经验，可以这样来理解，即把切线空间类比为3D世界中的局部空间。之所以要有局部空间，就是方便在制作模型时能够只专注于模型本身，而不必考虑模型在场景中可能出现的各种位置及朝向。在不同的位置、朝向下，模型中针对同一个顶点而言，其位置等信息是不一样的，如果没有局部空间，就需要为每种情况制作不同的模型，这样显然会很麻烦，甚至不可能，也很浪费，因为这些不同位置、朝向处的模型本质上是同一种。如果使用局部空间来定义模型，而通过为场景中不同模型指定各自的世界变换，就很容易地能够实现单个模型的重复利用。同样，法线贴图也是一个道理。一个模型的不同部位，甚至多个模型之间，可能会具有同样特点的表面，但显然由于其位置、朝向的不同，这些表面针对同一处的法线也是不一样的。比如一个正方体的六个表面，可以具有完全类似的特点，但各个面朝向不同，对应的法线也不再一样。没有切线空间，将不得不对每个表面制定单独的法线贴图，很浪费。如果把法线定义在切线空间，而针对每个面，都有其相应的切线空间，这样将可以使用同一张法线图来用于六个面。

那么，对于任意像素，从哪里可以获取其对应的切线空间呢？这时就要用到新的顶点格式，切线空间的信息正是通过在输入阶段由顶点传过来的，在像素着色阶段，每个像素对应的切线空间通过其所在三角形的三个顶点的切线空间进行插值得到。新的顶点格式即上节最后给出的：

[cpp]

struct

float3 normal : NORMAL;
float2 tex : TEXCOORD;
};

这里每个顶点除了位置坐标、纹理坐标外，还存放了法线、切线向量。而切线空间TBN需要三个向量。不过这里为了节省资源占用，只提供了切线与法线信息，另外一维bitangent可以在运行时通过该两向量的叉乘得到。相应的HLSL代码如下所示：

[cpp]

//Get TBN space float3 B = cross(N, T);

注意这里的法线不再是我们后面进行光照计算用到的法线，光照计算所用到的所有法线都是从法线图中获取的，这里的法线只是用来代表该顶点所在切线空间。

代码中第一行直接获取切线空间的法线部分（N），注意前提是要保证法线是已经经过归一化的。

第二行的目的是获取切线空间的切线部分（T），这里使用了一点小技巧，主要是为了保证切线与法线的相互垂直关系。因为在经过顶点着色器中的世界变换后，原本相互垂直的T与N可能由于精度的关系而不再垂直，这里需要来对它们进行一下修正，以相互满足垂直关系。方法即如上：normalize(pin.tangent - N * pin.tangent * N);

第三行通过对N、T进行叉乘，从而得到了切线空间的bitangent向量。注意进行叉乘的N和T的先后顺序！绝对不能是T x N！

有了切线空间的三个向量，我们也就得到了从切线空间到世界空间的转换矩阵了，即：

有了这个矩阵，我们继而可以很方便把从法线图读取到的法线转换到世界空间中了：

[cpp]

float3x3 T2W = float3x3(T, B, N);

normal = g_normalMap.Sample(samplerTex, pin.tex).rgb;
normal = normalize(mul(normal, T2W));

第一行通过切线空间T、B、N向量直接得到从切线空间到世界空间的变换矩阵。float3x3类型有接受三个三维行向量的构造函数，以利用三个行向量获得一个3x3矩阵。

第二行即之前介绍的把法线的每一维从[0, 1]区间转换到[-1, 1]区间。

第三行通过刚得到的切线空间到世界空间的矩阵T2W（Tangent to World），把读取到的法线转换到世界空间。

4. 小结及完整的pixel shader

好了，到这步为止，我们梦寐以求的法线得到了，法线映射的所有工作也就此结束了~

之后所有的像素着色器代码与之前的完全一样。本质上讲，上面介绍到的所有这些内容，其实特等效于以前代码中的：

[cpp]

float3 normal = normalize(pin.normal);

后面要做的即使用这个法线进行光照计算、纹理处理、雾效等过程了。不同之处仅仅是这里通过从纹理中读取法线来代替了之前直接从像素中获取经过插值的法线。

为了更清晰地展示法线映射在像素着色器中的应用，这里给出完整的pixel shader：

注意：这段代码中还有一些尚未进行介绍的内容，比如parallax mapping（法线映射的进阶），shadow mapping（生成阴影的常用算法之一）。暂时可以把这些内容忽略，以更好的关注normal mapping部分。

[cpp]

//Pixel shader numLights,

uniform useTexture,
alphaClipEnable,
uniform useNormalMap,
useParallaxMapping,
uniform useShadowMap,
pcfShadowEnable,
uniform useReflection,
fogEnable
): SV_TARGET
dist = length(toEye);
float3 normal = normalize(pin.normal);
(useParallaxMapping)
height = g_normalMap.Sample(samplerTex,pin.tex).a;
float3x3 W2T = transpose(float3x3(T,B,N));
float2 offset = toEyeTangent.xy * height;
(useNormalMap)
normal = normalize(mul(normal, T2W));
(useTexture)
(numLights > 0)
{
float3 shadowFactor = {1.f, 1.f, 1.f};
(useShadowMap)
{
(pcfShadowEnable)
( i=0; i<numLights; ++i)
{
color = color * (ambient + diffuse) + specular;
(fogEnable)
factor = saturate((dist - g_fogStart) / g_fogRange);
(useReflection)
{
color;
}

5. 示例程序

好了，法线映射的基础就介绍到这儿，最后是附带的一个简单示例程序，用于展示法线映射的效果。该示例程序中场景极其简单，仅仅是一个地面，加一个可以自由行走的照相机。可以通过按键1 -> 6来开启、关闭不同的效果，从而对使用法线映射与不使用法线映射的差别有更直观的感受。（按键‘3’ 和 ‘6’分别针对parallax mapping，暂时可以不管）。以下是几张运行截图，懒得下载代码的话可以从这儿的图中来感受下区别：

1. 仅仅光照计算下的一个平面地板：（按键 ‘1’）